Трапеция

Трапе́ция (от др.-греч. τραπέζιον — «столик») — это выпуклый четырёхугольник, характеризующийся наличием как минимум одной пары параллельных противоположных сторон (называемых основаниями), в то время как остальные две стороны (боковые стороны или ноги) могут быть непараллельными^[1].

История и происхождение

Античные корни

Лингвистические корни термина восходят к древнегреческому слову др.-греч. τραπέζιον, означающему «столик», которое, в свою очередь, происходит от др.-греч. τράπεζα — «стол»^[2]. В русском языке от того же корня образовалось слово «трапеза», обозначающее процесс принятия пищи или монастырскую столовую.

Систематическое изучение трапецевидных форм началось в эпоху античности. У Евклида трапецией назывался четырёхугольник, который не является параллелограммом (то есть не квадрат, не прямоугольник и не ромб). Современное определение (с одной парой параллельных сторон) появилось позже.

Особенно значимым стал вклад неоплатоника Прокла в середине V века нашей эры. Он приписывал Посидонию (около 100 года до н. э.) более богатую систему категорий. В этой схеме четырёхугольник мог быть параллелограммом или непараллелограммом.

Современные определения

Современная математическая наука предлагает два основных подхода к определению трапеции. Эксклюзивное определение рассматривает трапецию как четырёхугольник с точно одной парой параллельных сторон. При таком определении параллелограммы, включая ромбы, прямоугольники и квадраты, не считаются трапециями.

Инклюзивное определение классифицирует как трапецию любой четырёхугольник с как минимум одной парой параллельных сторон. В инклюзивной схеме классификации определения являются иерархическими: квадрат — это тип прямоугольника и тип ромба, прямоугольник или ромб — это тип параллелограмма, и каждый параллелограмм — это тип трапеции.

Профессиональные математики и учебники геометрии для высшего образования почти всегда предпочитают инклюзивные определения и классификации, поскольку они упрощают формулировки и доказательства геометрических теорем. В начальном и среднем образовании определения прямоугольника и параллелограмма также почти всегда инклюзивные, но эксклюзивное определение трапеции встречается часто. Для избежания путаницы некоторые источники используют термин «собственная трапеция»^[3] для описания трапеций с точно одной парой параллельных сторон, по аналогии с использованием слова «собственный» в некоторых других математических объектах.

Классификация и типы

Геометрическая классификация трапеций основывается на характеристиках боковых сторон и углов:

равнобедренная трапеция — фигура с равными боковыми сторонами и осью симметрии;
прямоугольная трапеция — содержит два смежных прямых угла;
касательная трапеция — обладает вписанной окружностью^[4].

Характеризующие свойства

Эквивалентные признаки

Для выпуклого четырёхугольника следующие свойства эквивалентны, и каждое означает, что четырёхугольник является трапецией:

Угол между стороной и диагональю равен углу между противоположной стороной и той же диагональю.
Диагонали пересекаются взаимно в том же отношении (это отношение равно отношению между длинами параллельных сторон).
Диагонали разрезают четырёхугольник на четыре треугольника, из которых одна противоположная пара имеет равные площади.
Произведение площадей двух треугольников, образованных одной диагональю, равно произведению площадей двух треугольников, образованных другой диагональю^[5].

Дополнительно действуют условия:

площади S и T некоторых двух противоположных треугольников из четырёх треугольников, образованных диагоналями, удовлетворяют уравнению:

{\sqrt {K}}={\sqrt {S}}+{\sqrt {T}}

где K — площадь четырёхугольника;

середины двух противоположных сторон трапеции и пересечение диагоналей лежат на одной прямой;
углы в четырёхугольнике ABCD удовлетворяют условию: sin A sin C = sin B sin D.

Угловые свойства

Косинусы двух смежных углов в сумме дают 0, как и косинусы двух других углов. Котангенсы двух смежных углов также дают в сумме 0, как и котангенсы двух других смежных углов^[3].

Одна из биссектрис делит четырёхугольник на два четырёхугольника равных площадей. Удвоенная длина биссектрисы, соединяющей середины двух противоположных сторон, равна сумме длин других сторон.

Основные свойства

Углы и стороны

Сумма углов, прилежащих к каждой боковой стороне трапеции, равна 180°, что следует из свойства секущей при параллельных прямых. Это создаёт внутреннюю симметрию угловых соотношений в пределах фигуры^[1].

Отношение боковых сторон равно отношению синусов противолежащих им углов:

{\frac {c}{d}}={\frac {\sin D}{\sin C}}

Это позволяет вычислять неизвестные параметры при частичной информации о фигуре.

Равнобедренные трапеции демонстрируют дополнительные закономерности: углы при любом основании равны между собой, сумма противоположных углов составляет 180°, диагонали равны по длине.

Высота

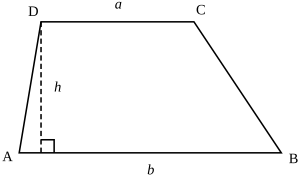
Высота — это перпендикулярное расстояние между основаниями. В случае, когда два основания имеют разные длины (a ≠ b), высота трапеции h может быть определена по длине её четырёх сторон по формуле:

h={\frac {\sqrt {(p-2a)(p-2b)(p-2b-2d)(p-2b-2c)}}{2|b-a|}}

,

где c и d — длины ног и p = a+b+c+d.

Более точная формула высоты через стороны имеет вид^[1]:

h={\sqrt {c^{2}-{\frac {1}{4}}\left({\frac {c^{2}-d^{2}}{b-a}}+b-a\right)^{2}}}

где b — большее основание, a — меньшее основание, c и d — боковые стороны.

Для равнобедренной трапеции формула высоты упрощается до

h={\sqrt {c^{2}-{\frac {1}{4}}(b-a)^{2}}}

поскольку c² — d² = 0.

Диагонали

Диагонали трапеции d₁ и d₂^[4] связаны со сторонами основным соотношением d₁² + d₂² = 2ab + c² + d². Их можно выразить в явном виде:

d_{1}=AC={\sqrt {ab+d^{2}+{\frac {b(c^{2}-d^{2})}{b-a}}}}

d_{2}=BD={\sqrt {ab+c^{2}-{\frac {b(c^{2}-d^{2})}{b-a}}}}

Если известны боковые стороны и диагонали, то основания выражаются формулами:

a={\sqrt {\frac {(c^{2}-d_{1}^{2})^{2}-(d_{1}^{2}-d_{2}^{2})^{2}}{2(c^{2}-d_{1}^{2}+d_{1}^{2}-d_{2}^{2})}}}

b={\sqrt {\frac {(c^{2}-d_{2}^{2})^{2}-(d^{2}-d_{1}^{2})^{2}}{2(c^{2}-d^{2}-d_{1}^{2}+d_{2}^{2})}}}

При известных основаниях и диагоналях боковые стороны определяются как:

c={\sqrt {\frac {a(d_{2}^{2}-b^{2})+b(d_{1}^{2}-a^{2})}{a+b}}}

d={\sqrt {\frac {a(d_{1}^{2}-b^{2})+b(d_{2}^{2}-a^{2})}{a+b}}}

Если известна высота h, то диагонали вычисляются по расширенным формулам:

d_{1}=AC={\sqrt {ab+d^{2}+{\frac {b(c^{2}-d^{2})}{b-a}}}}

d_{2}=BD={\sqrt {ab+c^{2}-{\frac {b(c^{2}-d^{2})}{b-a}}}}

Если трапеция разделена на четыре треугольника диагоналями AC и BD, пересекающимися в O, то площадь △AOD равна площади △BOC. Произведение площадей △AOD и △BOC равно произведению площадей △AOB и △COD.

Отношение площадей каждой пары смежных треугольников равно отношению между длинами параллельных сторон. Если отношение оснований равно K, то отношение площадей треугольников, прилежащих к основаниям, равно K²^[6].

Точка пересечения диагоналей трапеции

Специальные линии и точки

Замечательные прямые

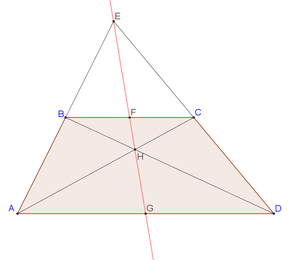
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой. Прямая Ньютона для трапеции совпадает с её средней линией^[3].

Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований. Линия, проходящая через пересечение диагоналей и пересечение продолжений непараллельных сторон, делит каждое основание пополам.

Особые отрезки

Длина отрезка s, соединяющего середины оснований трапеции, вычисляется по формуле

s={\frac {\sqrt {2(c^{2}+d^{2})-(a-b)^{2}}}{2}}

Если через точку пересечения диагоналей трапеции провести прямую, пересекающую основания, то точки пересечения её с основаниями — две из четырёх вершин параллелограмма. Все вершины этого параллелограмма лежат на сторонах трапеции по одной на каждой стороне, а стороны параллельны диагоналям данной трапеции. Два отрезка между боковой стороной трапеции и диагональю трапеции, которые диагонали отсекают от диагонали указанного параллелограмма, равны между собой^[7].

Неравенства

Геометрические параметры трапеции связаны системой неравенств^[8]:

Неравенство для сторон трапеции: сумма боковых сторон больше модуля разности оснований — AB + CD > |AD — BC|.
Неравенство для диагоналей: сумма диагоналей больше суммы оснований — AC + BD > AD + BC.
Дополнительное неравенство для сторон: модуль разности боковых сторон меньше модуля разности оснований — |AB — CD| < |AD — BC|.

Эти неравенства обеспечивают геометрическую реализуемость фигуры и служат критериями проверки корректности задаваемых параметров.

Равнобедренная трапеция

Признаки равнобедренности

Математическое определение равнобедренной трапеции основывается на системе взаимозаменяемых критериев, каждый из которых может служить как признаком, так и следствием изосцельной структуры фигуры. Фундаментальным геометрическим свойством является существование оси симметрии — прямой, проходящей через центральные точки оснований и образующей с ними прямые углы, что эквивалентно взаимной перпендикулярности отрезков, соединяющих середины противолежащих сторон.

Характерной особенностью служит деление большего основания высотой на два сегмента, один из которых численно соответствует полусумме длин оснований, а другой — их полуразности. Угловые характеристики подчиняются строгим закономерностям: углы при каждом основании попарно конгруэнтны, противолежащие углы в сумме образуют 180°, а диагонали демонстрируют равенство длин и симметричность углового положения^[4].

Специальные свойства

Визуально-геометрическое свойство равнобедренной трапеции проявляется в том, что любое из оснований «видимо» под одинаковым углом из каждой вершины противоположного основания, что связано с возможностью вписания фигуры в окружность и её связью с антипараллелограммом через соответствующие геометрические трансформации.

Когда диагонали образуют прямой угол в точке пересечения, высота принимает значение, равное среднему арифметическому длин оснований, а для любой равнобедренной трапеции ABCD с параллельными AD и BC и равными AB = CD справедливо соотношение AC² = AD · BC + AB²^[8].

Вписанная окружность

Условия существования

Геометрическая возможность размещения окружности внутри трапеции с касанием всех четырёх сторон определяется фундаментальным равенством периметральных сегментов: сумма длин параллельных оснований должна соответствовать сумме длин непараллельных сторон, что математически выражается условием a + b = c + d. При выполнении данного критерия средняя линия трапеции численно равна половине суммы боковых сторон, что представляет собой геометрическое следствие касательных свойств^[4].

Центральная точка вписанной окружности характеризуется особым угловым отношением к боковым сторонам: каждая из них визуально воспринимается из центра под прямым углом в 90°. Существенным является то, что обратное утверждение также справедливо — если трапеция допускает вписание в неё окружности (описанная трапеция), то она обязательно обладает равнобедренной структурой.

Параметры вписанной окружности

Радиальные характеристики вписанной окружности для трапеции, удовлетворяющей условию a + b = c + d, представимы через различные геометрические параметры:

r={\frac {h}{2}}

r={\frac {\sqrt {ab}}{2}}

r={\frac {\sqrt {d^{2}-l^{2}}}{2}}

Точка касания окружности с любой боковой стороной создаёт два сегмента v и w, связанные с радиусом соотношением

r={\sqrt {vw}}

что демонстрирует среднегеометрическую природу радиуса относительно касательных отрезков.

Пространственное положение центра окружности определяется пересечением двух специфических линий: высоты, проведённой через точку пересечения диагоналей, и средней линии трапеции. Эта локализация отражает симметрийные свойства касательной конфигурации.

Формулы для описанной трапеции

Боковые стороны c ≤ d описанной трапеции допускают аналитическое выражение через параметры оснований a, b и радиус r:

c={\frac {a+b}{2}}-{\frac {|a-b|}{2}}{\sqrt {1-{\frac {4r^{2}}{ab}}}}

Обратная зависимость связывает радиус с основаниями и углом между диагоналями:

d={\frac {a+b}{2}}+{\frac {|a-b|}{2}}{\sqrt {1-{\frac {4r^{2}}{ab}}}}

r={\frac {2ab(a+b)}{(a-b)^{2}\cot \theta }}

Структурное ограничение описанной трапеции выражается неравенством a < c ≤ d < b, указывающим на строгий порядок длин элементов. Расстояние между точками касания вписанной окружности с боковыми сторонами определяется формулой

l={\frac {2abr}{\sqrt {(ab)^{2}+((a-b)r)^{2}}}}

Углы в описанной трапеции

Противолежащие углы A и C описанной трапеции связаны с основаниями через котангенсы половинных углов:

{\frac {b}{a}}={\frac {\cot {\frac {A}{2}}}{\cot {\frac {C}{2}}}}

Площадь такой трапеции выражается через внутренние углы при основании и радиус вписанной окружности:

S=2r^{2}\left({\frac {1}{\sin \alpha }}+{\frac {1}{\sin \beta }}\right)

Угол θ между диагоналями, охватывающий боковую сторону во внутренней области, ограничен неравенством

\arccos \left[{\frac {(k-1)^{2}}{k^{2}+6k+1}}\right]\leq \theta <{\frac {\pi }{2}}

где k представляет отношение большего основания к меньшему. Нижняя граница этого неравенства достигается исключительно в равнобедренных описанных трапециях.

Прямоугольная описанная трапеция

Специфическими свойствами обладают прямоугольные трапеции с вписанной окружностью: диаметр такой окружности численно соответствует среднему гармоническому длин оснований. Угол между диагоналями определяется соотношением

\tan \theta =2\left({\frac {a+b}{a-b}}\right)^{2}

и принимает значения из интервала

\arctan 2<\theta <{\frac {\pi }{2}}

Радиус вписанной окружности для любой описанной трапеции ограничен сверху величиной

r\leq {\frac {\sqrt {ab}}{2}}

где равенство достигается только для равнобедренных конфигураций, что подчёркивает особый статус симметричных трапеций в теории вписанных окружностей.

Описанная окружность

Радиус окружности, охватывающей равнобедренную трапецию, определяется через боковую сторону c и основания a, b по формуле:

R=c{\sqrt {\frac {ab+c^{2}}{4c^{2}-(a-b)^{2}}}}

Угловые характеристики диагоналей такой трапеции связаны с основаниями соотношением:

\cos \theta ={\frac {(a-b)^{2}}{a^{2}+6ab+b^{2}}}

что отражает зависимость внутренней геометрии от пропорций параллельных сторон^[4].

Вычисление площади

Классические формулы

Метрические характеристики трапециальной области базируются на произведении средней длины параллельных сторон и перпендикулярного расстояния между ними^[9]:

S={\frac {(a+b)h}{2}}

Альтернативная запись через среднюю линию m даёт S = mh, где обе формулы математически идентичны вследствие равенства m = (a+b)/2, выражающего среднеарифметическую природу медианы трапеции.

Тригонометрический подход к вычислению площади использует среднюю линию m, боковую сторону c и прилежащий угол α в формуле S = mc sin α. Данное выражение является результатом применения синусоидальных соотношений к треугольникам, образуемым высотами трапеции при пересечении с боковыми сторонами. Универсальность формулы обеспечивается свойством sin α = sin(180° — α), позволяющим использовать любой из двух углов, смежных с выбранной боковой стороной.

Формула Бхаскары и её развитие

Историческое значение имеет формула VII века, разработанная индийским математиком Бхаскарой I^[10]. Формула, где a < b — основания, c и d — боковые стороны трапеции:

S={\frac {a+b}{4(b-a)}}{\sqrt {(a+c+d-b)(a+d-b-c)(a+c-b-d)(b+c+d-a)}}

Альтернативная запись той же формулы:

S={\frac {a+b}{2}}{\sqrt {c^{2}-{\frac {1}{4}}(b-a)^{2}}}

Эта формула может быть разложена в более симметричную версию:

S={\frac {a+b}{4|b-a|}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}

Когда одна из параллельных сторон сжалась в точку (скажем, a = 0), эта формула сводится к формуле Герона для площади треугольника.

Альтернативные формулы

Другая эквивалентная формула для площади, более близко напоминающая формулу Герона:

S={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}}

где

s={\frac {a+b+c+d}{2}}

— полупериметр трапеции.

Эта формула похожа на формулу Брахмагупты, но отличается от неё тем, что трапеция может не быть циклической (вписанной в окружность). Формула также является частным случаем формулы Бретшнайдера для общего четырёхугольника.

Из формулы Бретшнайдера следует^[11]:

S={\sqrt {{\frac {(ab^{2}-a^{2}b-ad^{2}+bc^{2})(ab^{2}-a^{2}b-ac^{2}+bd^{2})}{4(b-a)^{2}}}-\left({\frac {c^{2}+d^{2}-a^{2}-b^{2}}{4}}\right)^{2}}}

Разделение площади

Биссектриса, соединяющая параллельные стороны, делит площадь пополам. Более общий случай: любая линия, проведённая через середину медианы параллельно основаниям и пересекающая основания, делит площадь пополам.

Любой треугольник, соединяющий два конца одной ноги с серединой другой ноги, также составляет половину площади.

Средняя линия m разбивает фигуру на две трапеции, площади которых соотносятся как.

{\frac {S_{1}}{S_{2}}}={\frac {3a+b}{a+3b}}

По свойству треугольников △AHD и △BHC в трапеции ABCD:

S=\left({\sqrt {S_{\Delta AHD}}}+{\sqrt {S_{\Delta BHC}}}\right)^{2}

Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону^[5].

Площадь равнобедренной трапеции

Площадь равнобедренной трапеции с радиусом вписанной окружности, равным r, и любым из углов трапеции α:

S={\frac {4r^{2}}{\sin \alpha }}

Площадь равнобедренной трапеции через диагональ d, боковую сторону l и угол при основании α:

S=l{\sqrt {d^{2}-(l\sin \alpha )^{2}}}\sin \alpha

Площадь равнобедренной трапеции:

S=(b-c\cos \gamma )c\sin \gamma =(a+c\cos \gamma )c\sin \gamma

где c — боковая сторона, b — большее основание, a — меньшее основание, γ — угол между большим основанием и боковой стороной.

Площадь равнобедренной трапеции через её стороны^[4]:

S={\frac {a+b}{2}}{\sqrt {c^{2}-{\frac {1}{4}}(b-a)^{2}}}

Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты: S = h². В этом случае средняя линия совпадает по длине с высотой трапеции, то есть m = h.

Центры и точки

Центр площади (центр масс для однородной пластинки) лежит вдоль отрезка, соединяющего середины параллельных сторон, на перпендикулярном расстоянии x от более длинной стороны b, определяемом по формуле^[12]:

x={\frac {h}{3}}\cdot {\frac {2a+b}{a+b}}

Центр площади делит этот отрезок в отношении (взятом от короткой к длинной стороне) (a+2b)/(2a+b). Если биссектрисы углов A и B пересекаются в P, а биссектрисы углов C и D пересекаются в Q, то PQ = |AD + BC — AB — CD|/2.

Практические применения

Численное интегрирование

В математическом анализе определённый интеграл функции f(x) может быть численно аппроксимирован как дискретная сумма путём разбиения интервала интегрирования на небольшие однородные интервалы и аппроксимации значения функции на каждом интервале как среднего значений на его концах:

\int _{a}^{b}f(x)\,dx\approx \sum _{k=1}^{N}{\frac {1}{2}}\left(f(x_{k-1})+f(x_{k})\right)\Delta x

где N — количество интервалов,

x_{0}=a,\quad x_{N}=b

\Delta x={\frac {b-a}{N}}

Графически это равносильно аппроксимации области под графиком функции совокупностью трапеций, поэтому этот метод называется правилом трапеций^[13].

Визуальные эффекты

Когда любой прямоугольник рассматривается в перспективе с позиции, которая центрирована на одной оси, но не на другой, он кажется равнобедренной трапецией. Этот эффект называется эффектом краеугольного камня, поскольку арочные краеугольные камни обычно имеют трапецевидную форму. Например, когда прямоугольный фасад здания фотографируется с земли в позиции прямо перед ним с использованием прямолинейного объектива, изображение здания представляет собой равнобедренную трапецию.

К таким фотографиям иногда применяется «трапецеидальная трансформация» для восстановления прямоугольных форм. Видеопроекторы иногда применяют такую трапецеидальную трансформацию к записанному изображению перед проекцией, чтобы изображение, проецируемое на плоский экран, казалось неискажённым^[14].

Архитектурные применения

Трапецевидные двери и окна были стандартным стилем для инков, хотя их можно найти у более ранних культур того же региона, и они не обязательно возникли у них. Альмена, элемент зубчатых стен, характерный для мавританской архитектуры, имеет трапецевидную форму.

Переработка площади Кампидольо Микеланджело включала трапецию, окружающую эллипс, создающую эффект квадрата, окружающего круг, при виде в ракурсе с уровня земли^[15]. Кинематография использует трапеции противоположным образом, чтобы произвести чрезмерный эффект ракурса с точки зрения камеры, создавая иллюзию большей глубины комнаты в киностудии, чем физически имеет декорация.

Трапеции также использовались для создания визуальных искажений калигаризма. Каналы и дренажные канавы обычно имеют трапецевидное поперечное сечение.

Современные технологии

В биологии, особенно в морфологии и систематике, термины типа трапецевидный или трапециформный обычно полезны в описаниях определённых органов или форм. Трапеции иногда используются как графический символ. В схемных диаграммах трапеция — символ мультиплексора.

Равнобедренная трапеция используется для формы дорожных знаков, например, на второстепенных автомагистралях в Онтарио, Канада^[16]. В Храме Дендур в Метрополитен-музее в Нью-Йорке используются трапецевидные архитектурные элементы, характерные для египетской архитектуры.

Неевклидова геометрия

В сферической или гиперболической геометрии внутренние углы четырёхугольника не дают в сумме 360°, но четырёхугольники, аналогичные трапециям, параллелограммам и прямоугольникам, всё ещё могут быть определены. Дополнительно есть несколько новых типов четырёхугольников, не различимых в евклидовом случае^[17].

Сферическая или гиперболическая трапеция — это четырёхугольник с двумя противоположными сторонами, ногами. Каждый из двух смежных углов в сумме даёт одно и то же количество, другие две стороны — основания.

Как в евклидовой геометрии, специальные случаи включают равнобедренные трапеции, ноги которых равны (как и углы, смежные с каждым основанием), параллелограммы с двумя парами противоположных равных углов и двумя парами противоположных равных сторон, ромбы с двумя парами противоположных равных углов и четырьмя равными сторонами.

Примечания

↑ ^1,0 ^1,1 ^1,2 Погорелов А. В. Геометрия: учеб. для 7—11 кл. общеобразоват. учреждений. — 4-е изд. — М.: Просвещение, 1995. — С. 72. — 383 с. — ISBN 5-09-004557-7.
↑ Фасмер М. Этимологический словарь русского языка / пер. с нем. и доп. О. Н. Трубачёва. — 4-е изд., стер.. — М.: АСТ, 2009. — Т. 4. — ISBN 978-5-17-013959-0.
↑ ^3,0 ^3,1 ^3,2 Понарин Я. П. Элементарная геометрия. — 2-е изд., стер.. — М.: МЦНМО, 2008. — Т. 1: Планиметрия, преобразования плоскости. — 312 с. — ISBN 978-5-94057-398-2.
↑ ^4,0 ^4,1 ^4,2 ^4,3 ^4,4 ^4,5 Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Математика. Геометрия: учебник для 7—9 кл. общеобразовательных организаций. — М.: Просвещение, 2023. — С. 98—105. — 416 с. — ISBN 978-5-09-102538-5.
↑ ^5,0 ^5,1 Пиголкина Т. С. Свойства трапеции (неопр.). Заочная физико-техническая школа. МФТИ. Дата обращения: 7 сентября 2025. Архивировано 25 июня 2025 года.
↑ Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — С. 248—267. — 640 с. — ISBN 978-5-94057-304-3.
↑ Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — М.: Наука, 1986. — С. 89—103. — 224 с.
↑ ^8,0 ^8,1 Седракян Н. М., Авоян А. М. Неравенства: методы доказательства / пер. с армянского Г. В. Григоряна. — М.: Физматлит, 2002. — С. 178—195. — 256 с. — ISBN 5-9221-0273-7.
↑ Киселев А. П. Часть 1. Планиметрия. // Геометрия / под ред. Н. А. Глаголева. — М.: Физматлит, 2004. — С. 98—105. — 328 с. — ISBN 5-9221-0367-9.
↑ Bhaskara I. Laghubhaskariya (англ.) / English transl. by K. S. Shukla. — Lucknow, 1963.
↑ Байгонакова Г. А., Медных А. Д. О формуле Бретшнайдера для гиперболического четырёхугольника // Математические заметки СВФУ. — 2012. — Т. 19, № 1. — С. 12—19.
↑ Энхтайван М. Применение центра масс при решении геометрических задач // Международный школьный научный вестник. — 2022. — № 2.
↑ Демидович Б. П., Марон И. А. Основы вычислительной математики. — 3-е изд., испр. — М.: Наука, 1966. — 664 с.
↑ Sukthankar R., Stockton R. G., Mullin M. D. Automatic Keystone Correction for Camera-assisted Presentation Interfaces (англ.) // Proceedings of the 2nd international conference on Computer vision systems. — 2000. — October. — P. 607—614.
↑ Всеобщая история архитектуры / под ред. В. Ф. Маркузона (отв. ред.) и др.. — Москва: Академия архитектуры СССР, 1967. — Т. 5: Архитектура Западной Европы XV—XVI веков. Эпоха Возрождения. — 658 с.
↑ ГОСТ Р 52290-2004. Технические средства организации дорожного движения. Знаки дорожные. — Общие технические требования : национальный стандарт Российской Федерации. — М.: Стандартинформ, 2005. — С. 114.
↑ Широков П. А. Краткий очерк основ геометрии Лобачевского. — 2-е изд. — М.: Наука, 1983. — 80 с.

[:0-1] 1,0 ^1,1 ^1,2 Погорелов А. В. Геометрия: учеб. для 7—11 кл. общеобразоват. учреждений. — 4-е изд. — М.: Просвещение, 1995. — С. 72. — 383 с. — ISBN 5-09-004557-7.

[2] Фасмер М. Этимологический словарь русского языка / пер. с нем. и доп. О. Н. Трубачёва. — 4-е изд., стер.. — М.: АСТ, 2009. — Т. 4. — ISBN 978-5-17-013959-0.

[:1-3] 3,0 ^3,1 ^3,2 Понарин Я. П. Элементарная геометрия. — 2-е изд., стер.. — М.: МЦНМО, 2008. — Т. 1: Планиметрия, преобразования плоскости. — 312 с. — ISBN 978-5-94057-398-2.

[:2-4] 4,0 ^4,1 ^4,2 ^4,3 ^4,4 ^4,5 Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Математика. Геометрия: учебник для 7—9 кл. общеобразовательных организаций. — М.: Просвещение, 2023. — С. 98—105. — 416 с. — ISBN 978-5-09-102538-5.

[:3-5] 5,0 ^5,1 Пиголкина Т. С. Свойства трапеции (неопр.). Заочная физико-техническая школа. МФТИ. Дата обращения: 7 сентября 2025. Архивировано 25 июня 2025 года.

[6] Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — С. 248—267. — 640 с. — ISBN 978-5-94057-304-3.

[7] Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — М.: Наука, 1986. — С. 89—103. — 224 с.

[:4-8] 8,0 ^8,1 Седракян Н. М., Авоян А. М. Неравенства: методы доказательства / пер. с армянского Г. В. Григоряна. — М.: Физматлит, 2002. — С. 178—195. — 256 с. — ISBN 5-9221-0273-7.

[9] Киселев А. П. Часть 1. Планиметрия. // Геометрия / под ред. Н. А. Глаголева. — М.: Физматлит, 2004. — С. 98—105. — 328 с. — ISBN 5-9221-0367-9.

[10] Bhaskara I. Laghubhaskariya (англ.) / English transl. by K. S. Shukla. — Lucknow, 1963.

[11] Байгонакова Г. А., Медных А. Д. О формуле Бретшнайдера для гиперболического четырёхугольника // Математические заметки СВФУ. — 2012. — Т. 19, № 1. — С. 12—19.

[12] Энхтайван М. Применение центра масс при решении геометрических задач // Международный школьный научный вестник. — 2022. — № 2.

[13] Демидович Б. П., Марон И. А. Основы вычислительной математики. — 3-е изд., испр. — М.: Наука, 1966. — 664 с.

[14] Sukthankar R., Stockton R. G., Mullin M. D. Automatic Keystone Correction for Camera-assisted Presentation Interfaces (англ.) // Proceedings of the 2nd international conference on Computer vision systems. — 2000. — October. — P. 607—614.

[15] Всеобщая история архитектуры / под ред. В. Ф. Маркузона (отв. ред.) и др.. — Москва: Академия архитектуры СССР, 1967. — Т. 5: Архитектура Западной Европы XV—XVI веков. Эпоха Возрождения. — 658 с.

[16] ГОСТ Р 52290-2004. Технические средства организации дорожного движения. Знаки дорожные. — Общие технические требования : национальный стандарт Российской Федерации. — М.: Стандартинформ, 2005. — С. 114.

[17] Широков П. А. Краткий очерк основ геометрии Лобачевского. — 2-е изд. — М.: Наука, 1983. — 80 с.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]