Площадь (математика)

Наука
Математика
Тема	Площадь
Предмет изучения	сколько единичных квадратов и их частей заполняет плоскую фигуру
Основные направления	математика
Вспомогат. дисциплины	алгебра, геометрия, математический анализ, тригонометрия

Пло́щадь (в математике) — одна из количественных характеристик геометрических фигур, показывающая сколько единичных квадратов и их частей заполняет плоскую фигуру. Единичный квадрат — это квадрат со стороной, равной единице длины.

Свойства площади

Свойство аддитивности площади (на примере выпуклого многоугольника)

К основным свойствам площади относятся следующие её свойства:

1. положительность (значения площади выражаются только положительными числами);
2. аддитивность (площадь фигуры, составленной из нескольких частей, которые не имеют общих точек — не пересекаются, равна сумме площадей её частей):
3. инвариантность (значения площади при перемещениях не изменяются);
4. нормированность (площадь единичного квадрата равна квадрату его стороны).

Площадь плоских фигур

Основные формулы для вычисления площади некоторых плоских фигур

Название плоской фигуры	Формула	Обозначения	Изображение
Квадрат	$S=a^{2}$,$S={\frac {1}{2}}d^{2}$	a — длина стороны квадрата d — диагональ квадрата	Квадрат
Прямоугольник	$S=ab$	a и b — длины сторон прямоугольника	Прямоугольник
Параллелограмм	$S=ah$, $S=ab\sin C$,$S={\frac {1}{2}}d_{1}d_{2}\sin \theta$	a — основание, h — высота a и b — смежные стороны, $\angle C$ — угол между ними d1 и d2 — диагонали параллелограмма, $\angle \theta$ — угол между ними	Параллелограмм
Ромб	$S={\frac {1}{2}}d_{1}d_{2}$	AC=d1 и BD=d2 - диагонали ромба	Ромб
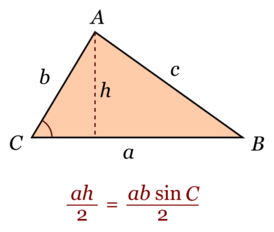
Треугольник	$S={\frac {1}{2}}ah$, $S={\frac {1}{2}}ab\sin C$, $S={\frac {abc}{4R}}$, $S={\frac {1}{2}}Pr$ $S={\sqrt {p(p-a)(p-b)(h-c)}}$	a — основание, h — высота a и b — смежные стороны, $\angle C$ — угол между ними a, b и c — стороны треугольника, R — радиус описанной окружности P — периметр треугольника, r — радиус вписанной окружности a, b и c — стороны треугольника, p — его периметр (формула Герона)	Треугольник
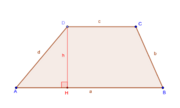
Трапеция	$S={\frac {1}{2}}(a+b)h$	a и b — основания, h — высота трапеции	Трапеция
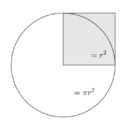
Круг	$S=\pi r^{2}$	r — радиус круга	Круг

Способы нахождения площади

Квадрируемая фигура с внешней и внутренней областью

Квадрируемые фигуры

Плоская фигура F произвольной формы квадрируема, если существуют такие многоугольные фигуры F₁ и F₂, что F₁ $\subset$ F $\subset$ F₂.

Под внешней площадью фигуры понимается множество элементарных квадратов, имеющих точную нижнюю границу, под внутренней — множество элементарных квадратов, имеющих точную верхнюю. Фигуру, с равными внешней и внутренней площадью, называют квадрируемой.

Если верхняя площадь фигуры совпадает с её нижней площадью, то эта величина называется площадью фигуры, а сама фигура — квадрируемой. На данном определении построена теория площадей плоских фигур, ограниченных простыми (то есть не пересекающими себя) контурами.

Площадь криволинейной трапеции

Аналитический способ

Площадь плоских фигур — так называемых криволинейных трапеций можно вычислить с помощью определённого интеграла по формуле $S=\int \limits _{a}^{b}f(x)dx$, где f(x) — функция, ограничивающая заданную фигуру сверху, x=a и x=b — прямые, ограничивающие её слева и справа соответственно, [a; b] — отрезок оси Ox, ограничивающий фигуру снизу.

Площадь плоской фигуры, ограниченных двумя кривыми y₁(x) и y₂(x) и прямыми x=a и x=b, ограничивающих её слева и справа соответственно можно вычислить с помощью определённого интеграла по формуле $S=\int \limits _{a}^{b}y_{1}(x)-y_{2}(x)dx$.

Если фигура, ограниченна замкнутым контуром, который встречается с каждой прямой, параллельной к оси Oy, не более чем в двух точках, то её площадь находят с помощью двойного интеграла по формуле $S=\iint \limits _{F}dxdy$.

Площадь поверхности

Площадь поверхности для многогранных поверхностей равна сумма площадей её плоских граней.

Площадей фигуры, расположенной на кривой поверхности, заданной уравнением z=f(x, y), может быть выражена двойным интегралом $S=\iint \limits _{D}{\sqrt {1+(f'_{x})^{2}+(f'_{y})^{2}}}dxdy$.

Единицы измерения площади

Таблица единиц площади в метрической системе мер:

1мм² $\longrightarrow$1см² $\longrightarrow$1дм² $\longrightarrow$1м² $\longrightarrow$1а $\longrightarrow$1га, где каждая следующая единица площади в 100 раз больше предыдущей.

Площади больших фигур измеряют в км².

1а = 100 м², 1га = 10000 м², 1км² = 1000000 м².

Литература

1. Высшая математика : учебное пособие / В. И. Белоусова, Г. М. Ермакова, М. М. Михалева, Н. В. Чуксина, И. А. Шестакова. — Екатеринбург : Изд-во Урал. ун-та, 2017.— Ч. II.— 300 с.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!