Геометрия

Геометрия — это фундаментальная наука, часть математики, которая изучает фигуры и их свойства на плоскости и в пространстве.

Геометрия и геометрические фигуры повсеместно изучаются с раннего возраста, начиная с детского сада. Затем знакомство с геометрий продолжается в школе. В ВУЗах происходит более углубленное изучение специальных разделов геометрии.

Определение геометрии

пример сложной геометрической задачи

Название «геометрия» происходит от греческих слов «гео» — земля и «метрео» — измеряю. Геометрия берёт свое начало именно с измерений на земле, вычисления площади плодородных участков. Также астрологи рассчитывали расположение различных небесных объектов и светил.

Геометрия не есть изолированная отрасль, не пересекающаяся с другими разделами математики. Дело состоит ровно наоборот. Многие задачи из алгебры, арифметики, математического анализа, теории дифференциальных уравнений, теоретической механики решаются как раз при помощи построений на плоскости и в пространстве, то есть путём применения геометрических методов. Более того, огромная часть уравнений решается геометрическим способом путем построений фигур или графиков функций.

Базовыми объектами в геометрии являются «точка», «луч», «прямая», «отрезок», «плоскость», «угол» и «фигура». Со своей стороны геометрия использует инструментарий алгебры и теории уравнений. Многие геометрические задачи на нахождение элементов фигур и площадей решаются путем сведения их к уравнениям. Геометрия также имеет дело и с числами, как и любая другая часть математики.

Базовые понятия в геометрии

Всё начинается с точки. Это простейшее понятие в геометрии. «Точка» на плоскости или в пространстве представляет собой неделимый объект, который занимает заданное местоположение, иными словами, имеющий определённые координаты. Если две точки имеют одни и те же координаты, то эти точки совпадают. Сравнивать точки между собой, как например мы сравниваем числа, какая из них больше или меньше, тяжелее или легче (как мы сравниваем массы предметов) в геометрии не имеет смысла. Все они равные или, иначе выражаясь, одинаковые, ни легче, ни тяжелее, ни меньше, не больше по размеру и весу. Поэтому точка — это некий абстрактный и типичный объект. Точки принято обозначать большими латинскими буквами A, B, C и др.

Если две точки не совпадают, их можно соединить линией. Линии бывают прямые или не прямые, то есть кривые. При этом две различные точки можно соединить только одной прямой, проходящей через эти точки.

угол в 1 радиан

Это является одной из основных аксиом геометрии. В самом деле, в классической геометрии Евклида, если провести через две точки вторую линию, отличную от первой прямой, то это будет уже не прямая, а кривая. Данный факт не трудно представить и визуализировать на листе бумаги.

«Луч» — это часть прямой, отложенная от точки (начала луча) только в одну строну. Луч иногда называют полупрямой. Иными словами, луч представляет собой прямую линию, имеющую начало, но не имеющую конца.

«Угол» представляет собой два луча, исходящих из одной точки. Углы делятся на острые (градусная мера менее 90 градусов), прямые (90 °), тупые (от 90 ° до 180 °), развернутые (180 °). Углы принято обозначать либо одной заглавной латинской буквой, обозначающей его вершину $\angle$ А, $\angle$ B, $\angle$ C и т. д. Либо тремя буквами $\angle$ ABC, $\angle$ MNK и т. п. Углы также принято измерять в радианах, при этом 180° это π радиан. 1 радиан — это центральный угол, длина дуги которого равна радиусу окружности. Пример угла в 1 радиан можно видеть на рисунке.

отрезки

«Отрезок» — это часть прямой, ограниченная двумя точками. Если одну точку принять за начало, а вторую точку принять за конец, то такой отрезок будет направленным и называться «вектором». Отрезки обозначаются двумя латинскими буквами, то есть обозначение начала и конца отрезка AB, CD и т. п. Пример отрезков можно видеть на рисунке.

«Плоскость» — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки. Понятие, знакомое каждому, при этом столь же важное в геометрии как точка и прямая. Плоскости обычно обозначают греческими буквами α, β и др.

Геометрические фигуры

Базовыми фигурами в геометрии на плоскости являются треугольник, четырёхугольник, многоугольник, окружность. В пространстве — это призма, пирамида, сфера, конус.

«Треугольник» — простейшая фигура в геометрии, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих вершины треугольника. Отрезки при этом будут называться сторонами треугольника. У треугольника три угла и три стороны. Поэтому можно выделить прямоугольные треугольники (один из углов — прямой), остроугольные треугольники (все углы — острые), тупоугольные треугольники (если один угол тупой). Замечательным свойством треугольника будет формула о сумме его углов, которая равна 180°. Иными словами, если α, β, γ — углы треугольника, то верно равенство α + β + γ =180°.

Треугольник ABC

Если классифицировать треугольники с позиции сторон, то треугольники делятся на равносторонние (все стороны равны), равнобедренные (две стороны из трех равны, но не равны третьей) и произвольные. В треугольнике против наибольшего угла лежит наибольшая сторона и наоборот. Огромное значение треугольники играют в геометрии благодаря тому, что почти любая фигура разбивается на треугольники каким-либо методом. Таким образом, чтобы уметь анализировать более сложные фигуры, нужно знать свойства треугольника.

Базовое значение в геометрии играет теорема Пифагора, которая гласит, что в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов: $a^{2}+b^{2}=c^{2}$. Для решения большинства задач в геометрии так или иначе используются теорема Пифагора.

«Четырёхугольник» — фигура, состоящая из четырёх вершин и четырёх отрезков, последовательно соединяющих его вершины, являющихся его сторонами, при этом никакие три вершины не лежат на одной прямой. Последнее требование позволяет исключить вырожденные четырёхугольники, которые представляют собой треугольники или прямые. Важными представителями четырёхугольников являются параллелограмм и трапеция, поскольку почти все остальные четырёхугольники можно анализировать на основе их свойств.

• Параллелограмм — четырёхугольник, у которого противоположные стороны попарно равны и параллельны.
• Трапеция — четырёхугольник, у которого две противоположные стороны параллельны и две другие не параллельны.

Наиболее популярными четырёхугольниками на практике являются квадраты, прямоугольники и ромбы, которые уже определяются на основе параллелограммов.

• Ромб — четырёхугольник, у которого все стороны равны.
• Прямоугольник — четырёхугольник, у которого все углы прямые.
• Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны.

Сфера с радиусом r и диаметром d

Любой многоугольник уже разбивается на вышеописанные фигуры, поэтому его свойства можно изучать на основе рассмотренных фигур. Особняком стоит окружность или круг. Введение понятие «окружности» или «равноудалённости» значительно расширяет функционал и угол зрения геометрической науки. В свою очередь широкое применение круга на практике заставляет геометров пристально изучать свойства окружности, чтобы найденные таким образом закономерности инженеры могли применить в промышленности и других практических областях.

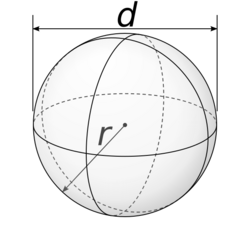
Окружность — это множество точек одной плоскости, равноудаленных от одной точки (центра окружности). При этом расстояние от любой точки окружности до её центра называется радиусом окружности или круга. Термин круг используется, если требуется включить все точки внутри окружности в одну фигуру. Отсюда следует, что окружность в отличие от круга не имеет площади. Но окружность является границей круга.

Если в определении окружности убрать требование на нахождение точек в одной плоскости, то получится сфера или шар.

• Сфера — это множество точек пространства, равноудаленных от одной точки (центра сферы). Сфера является границей шара.
• Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её верхними и нижними основаниями. Наиболее популярной призмой является куб.
• Пирамида — многогранник, основанием которого является многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
• Конус — геометрическая фигура в пространстве, образованная множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).

Виды геометрии

Геометрия как наука в свою очередь делится на разделы и виды:

• Планиметрия — геометрия, в которой изучаются свойства фигур и объектов в рамках одной плоскости. В качестве примеров таких фигур можно указать названные выше треугольник, трапеция, окружность.

задача из начертательной геометрии

• Стереометрия — геометрия, в которой изучаются свойства фигур и объектов в трехмерном пространстве. Здесь большое внимание уделяется углу между плоскостями (двугранный угол), а также фигурам — шар, пирамида, призма и др.
• Аналитическая геометрия — геометрия, в которой для изучения свойств геометрических объектов и фигур используется инструментарий алгебры, а именно метод координат. Например, плоские фигуры изучаются путем введения двумерных координат $(x;y)$ для каждой точки. Пространственные фигуры из стереометрии анализируются путем введения координат $(x,y,z)$. Например, уравнением прямой на плоскости служит уравнение $y=k*x+b$. Имея две прямые и два уравнения, их описывающие, можно найти точу пересечения данных прямых или доказать их параллельность. Треугольник можно задать координатами его вершин, а далее найти расстояние по формуле нахождения расстояния между двумя точками. После нахождения длин сторон можно найти площадь треугольника по формуле Герона $S={\sqrt {p(p-a)(p-b)(p-c)}}$, где p — полупериметр треугольника. В аналитической геометрии существуют признаки параллельности и перпендикулярности прямых и плоскостей.
• Начертательная геометрия — вид геометрии, где пространственные фигуры изучаются методом их проецирования на плоскости. Обычно такая геометрия изучается на инженерных специальностях в ВУЗах.
• Дифференциальная геометрия — это раздел высшей геометрии, где свойства фигур изучаются при помощи интегрального исчисления, при помощи инструментария линейной алгебры, дифференциальных уравнений. Основоположником данной геометрии является великий русский математик Н.И. Лобачевский (1792—1856). Данную геометрию принято называть неевклидовой геометрией, где аксиома о том, что через точку вне прямой на данной плоскости проходит только одна прямая параллельная данной, не верна.

Литература

• Бекаревич А. Н. Уравнения в школьном курсе математики. — Минск: Нар. асвета, 1968. — 152 с.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.
• Литцман В. Теорема Пифагора. — М., 1960.
• Скопец З. А. Геометрические миниатюры. — М., 1990
• В. О. Гордон, М. А. Семенцов-Огиевский «Курс начертательной геометрии», М., 1971 г.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!