Уравнение

Графическое изображение линейных уравнений

Уравне́ния — это самые распространённые сущности в математике, физике и других точных науках. Множество законов природы описывается с помощью уравнений. Состояния различных объектов также можно задать уравнением или несколькими уравнениями. Если уравнений более одного, то употребляют термин «система уравнений». Уравнения бывают различных типов и различной сложности, но каждый ученик начальной школы уже решает простейшие линейные уравнения. В высшей математике без уравнений не обходится ни один из её разделов. Можно с полной уверенностью утверждать, что уравнения — это язык математики и физики.

Определение уравнения

Уравнение — это равенство двух математических выражений с использованием буквенных обозначений, среди которых есть известные и неизвестные. Например, простейшими примерами уравнений будут $8-x=3$ или $y+a=6$, где x и у — неизвестные. Неизвестные (или их ещё можно назвать «переменными») в уравнениях обычно обозначаются латинскими буквами из конца алфавита $x,y$ и $z$. При этом начальными символами латинского алфавита $a,b,c$ обычно обозначаются не переменные, а постоянные или константы (или параметры).

Решение уравнения — это нахождение неизвестного переменного (или неизвестных переменных). Решить уравнение означает найти все корни уравнения или доказать, что корней не существует. Требуется именно доказательство факта несуществования корней. Если не удаётся найти корень или решающий считает, что корней нет лишь только потому, что не удалось их найти или так кажется самому решающему, то данная ситуация не является доказательством.

Корнем уравнения является значение неизвестного, при подстановке которого вместо неизвестного в искомое уравнение выполняется равенство (тождественное). Каждое уравнение необязательно имеет один корень. Может быть несколько случаев:

1.Уравнение не имеет корней. Примером уравнения, не имеющего корня (среди действительных чисел), будет $z^{2}=-5$. Действительно, любое число при возведении в квадрат будет неотрицательным и ни при каких обстоятельствах не получится −5.

2. Уравнение имеет более одного корня. Корнями уравнений, приведённых абзацем выше, будут $x=5$ в первом случае и $y=6-a$ во втором случае.

3. Уравнение имеет бесконечное количество корней. Примером уравнения с бесконечным числом корней будет $z*0=0$. При умножении любого числа на ноль в ответе получается тот же самый ноль.

Также существует множество уравнений с двумя и более неизвестными. В таком случае под корнем уравнения понимается набор из значений каждой неизвестной, при подстановке которого в исходное уравнение получается тождественное равенство. Например, $y^{2}+z^{2}=-1$ является отличным примером уравнения с двумя неизвестными y и z, при этом корней у данного уравнения не существует. Сумма двух неотрицательных чисел не может быть отрицательной.

А вот уравнение $x+y+z=17$ является примером уравнения с тремя неизвестными и, в отличие от предыдущего, данное уравнение имеет бесконечное количество корней. Это различные тройки чисел, дающие при сложении 17, например, {1;2;14}, {2; 3; 12} и т. д.

Примеры использования

Как было указано ранее, уравнения очень важны в точных науках. В самом деле, уравнения — это универсальный инструмент математики. Многие задачи задаются в виде уравнений и решаются с помощью уравнений. В этом смысле уравнения, как об этом было упомянуто выше, представляют ни что иное, как язык математики. Это можно показать на следующем примере. Пусть имеется прямоугольник, у которого длина превышает ширину в три раза. При этом площадь прямоугольника равна 27. Чему равны стороны прямоугольника и его периметр? Для этих целей нужно данные условия задачи перевести на язык выражений и уравнений. Поскольку стороны прямоугольника неизвестны, с ними невозможно работать, пока они не обозначены каким-то символом. Пусть $x$ — это ширина, тогда очевидно, что длина будет составлять $3*x$. А если рассмотреть произведение длины и ширины, то получается площадь. Иными словами: $x*3*x=27$. А это ведь и получилось уравнение, то есть равенство с неизвестной переменной $x$. Решая данное уравнение, находим его корни $x=3$ и $x=-3$ (для решения нужно поделить обе части на 3, а далее извлечь квадратный корень из обеих частей уравнения). Однако здесь $x$ — это ширина прямоугольника, которая не может выражаться отрицательным числом. Поэтому следует немедленный вывод, что −3 для нас является посторонним корнем. Часть корней зачастую на практике таким образом вычёркиваются и отсеиваются. Но это не должно смущать, поскольку здесь не решается уравнение в чистом его виде, уравнение служит для формулирования математической задачи.

Таким образом, можно подсчитать, что длина прямоугольника составляет 9, а его периметр будет равен 24. Получается, что абзацем выше было применено уравнение во благо прямоугольника. Правда, у прямоугольника площадь составляла ровно 24, а одна из сторон была ровно в 3 раза больше другой. Можно применить подобное уравнение и подобный подход к более широкому классу прямоугольников. Например, если у прямоугольника площадь не 27, а 100. При этом одна из его сторон не в 3, а в 4 раза больше. Данный подход также нужно применять на основе уравнений. Здесь получается уравнение $x*4*x=100$, решив которое, находятся стороны уже нового прямоугольника: 5 и 20.

Но красота математики и популярность уравнений состоит в том, что аналогичное уравнение можно применить вообще к общему классу прямоугольников. В самом деле, пусть площадь прямоугольника задаётся буквой $S$, а одна из сторон больше другой в $k$ раз. Обозначая меньшую из сторон прямоугольника за $x$, получается следующее уравнение: $x*k*x=S$ или $k*x^{2}=S$.

Решая данное уравнение относительно $x$, получается, что меньшая из сторон составляет ${\sqrt {S/k}}$.

Смысл подобного подхода к решению практических задач с помощью уравнения заключается в том, что возможно для любых значений $S$ и $k$ быстро находить стороны прямоугольника. Для этого вовсе не понадобится заново составлять уравнение, а можно просто воспользоваться общей формулой ответа. Например, бывают такие прямоугольники в виде узкой и длинной полоски, где длина превышает ширину в 1 млн раз, а площадь может быть любой, даже 1 млрд. И для нахождения сторон нам просто достаточно подставить 1 млн и 1 млрд в общую формулу ответа.

Выше было наглядно показано, как применяются уравнения в случае с прямоугольниками, то есть как уравнения используются в геометрии. Однако похожим образом их можно применять и в других задачах, например, в задачах на движения, на совместную работу и т. п.

Равносильные уравнения

Два уравнения называются «равносильными», если они имеют равные корни или, выражаясь более строго, множество их корней совпадают. Например, если первое уравнение имеет корни 1 и 18, а другое уравнение имеет также два корня 1 и 18, то такие уравнения — равносильные. А вот если одно уравнение имеет корни 1 и 18, а второе уравнение имеет три корня 1, 18 и −1, то такие уравнения уже не являются равносильными.

Очевидно, что уравнения $1-x=7$ и $x+8=2$ являются равносильными, поскольку оба имеют единственный корень −6. А вот уравнения ${\sqrt {x}}=3$ и $x^{2}=81$ не являются равносильными хотя бы потому, что имеют разное число корней.

Область допустимых значений

Область определения или область допустимых значений уравнения — это множество значений переменной, при которых уравнение имеет смысл. Например, для уравнения ${\frac {1}{2x}}+{\frac {x}{x+1}}={\frac {1}{2}}$это все числа, отличные от 0 и -1, поскольку на ноль делить нельзя. Обычно после нахождения каждого корня делается проверка, входит ли корень в область допустимых значений или нет. В случае, если не входит — данный корень является ложным и в ответ не включается.

Виды уравнений

Существует великое множество различных типов уравнений как в математике, так и в физике. Здесь лишь вкратце перечислим их.

• Линейные уравнения — это уравнения вида $kx+b=0$, о которых речь шла выше, например, $15-20z=-2$
• Квадратные уравнения вида $ax^{2}+bx+c=0$. Квадратным уравнениям огромное внимание уделяется в курсе средней школы в программе алгебры.
• Биквадратные уравнения $ax^{4}+bx^{2}+c=0$, которые решаются введением новой переменной $z=x^{2}$ и приведением к квадратному уравнению.
• Уравнения высоких (3 и более) степеней, например, уравнение пятой степени в общем виде имеет следующую структуру $ax^{5}+bx^{4}+cx^{3}+dx^{2}+ex+k=0$
• Дробные уравнения вида $A(x)/B(x)=0$, где A(x) и B(x) — многочлены.
• Тригонометрические уравнения — это уравнения с участием тригонометрических выражений, простейшим примером которых будут $sin(x),cos(z)$. Например, уравнение $sin(x)-4*cos^{2}(x)-7=0$ является примером тригонометрического уравнения, которое решается введением новой переменной $z=sin(x)$ и приведением к обычному квадратному уравнению.
• Логарифмические уравнения — это любые уравнения с использованием логарифма от неизвестной переменной вида $\log _{a}x$ или $\log _{x}b$. Примером логарифмического уравнения будет $\log _{2}x=3+\log _{8}x^{2}$
• Показательные уравнения — это уравнения, где неизвестное содержится в показатели степени. Это всевозможные уравнения с использованием выражений вида $a^{x}$. Примером показательного уравнения будет $3^{x}+4*3^{2x}=-8$
• Дифференциальные уравнения — это уравнения, где в качестве неизвестной фигурируют функции, при этом в записи уравнения присутствуют и производные (разных порядков) от данных функций. Данные уравнения изучаются в разделе высшей математики. Примером дифференциального уравнения будет $\left(y''\right)^{2}+2y'+7y-x^{3}=0$.
• Матричные уравнения — уравнения, где в качестве переменных используются «матрицы» (прямоугольные таблицы чисел). При этом уравнения относительно одной переменной первой степени — это простейший вид матричных уравнений 1*1. Данные уравнения изучаются в курсе высшей математики (алгебра и линейная алгебра).

Общие способы решений уравнений

Графическое решение квадратного уравнения

Общий принцип решения любого типа уравнения заключается в преобразовании обеих частей уравнения и приведении уравнения к простейшему или стандартному виду. Простейшие уравнения уже имеют формулу нахождения корней.

Например, для квадратных уравнений вида $ax^{2}+bx+c=0$ существует формула нахождения корней с помощью дискриминанта. Для тригонометрических уравнений простейшими будут уравнения вида $sin(x)=a,cos(x)=b,tg(x)=c$. Для логарифмических уравнений простейшим видом будет $\log _{a}x=b$, для показательных уравнений простейшим видом будет $a^{x}=b$.

В преобразовании уравнения к стандартному типу поможет введение новой переменной (например, как при решении биквадратных уравнений вводится новая переменная $z=x^{2}$). Также помогает разложение одной из частей уравнения на множители и приведение к типу $A(x)*B(x)=0$, где А и В это функции от переменной.

В процессе преобразования уравнения следует помнить об области допустимых значений. Дело в том, что часть преобразований (например, возведение обеих частей в квадрат) может добавить дополнительных ложных корней. Поэтому после нахождения корней их обязательно требуется проверить на вхождение в область допустимых значений. Если при этом какой-либо корень не входит в данную область, он будет являться ложным корнем.

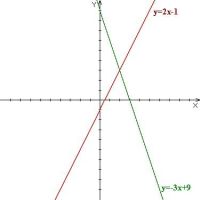
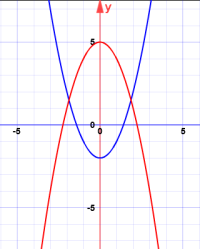
Также существует графический способ решения уравнений. Данный способ заключается в построении графиков функций правых и левых частей уравнения и нахождения точек пересечения. Здесь полезно привести исходное уравнение к виду $f(x)=g(x)$, где f и g — функции, графики которых могут быть построены.

Химические уравнения

Существуют химические уравнения.

Литература

• Бекаревич А. Н. Уравнения в школьном курсе математики. — Минск: Нар. асвета, 1968. — 152 с.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.

Ссылки

• Уравнение // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!