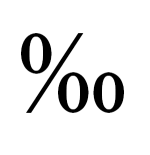Число

Разнообразие чисел

В повседневной жизни, в математике, в точных науках почти повсеместно используются числа. При помощи чисел происходит измерение различных величин. Числа помогают количественно характеризовать различные свойства предметов. Например, цены на продукты в магазине, массу и габариты предметов вокруг нас, возраст людей, расстояние между городами и т. п. Всё это и не только это выражается с помощью чисел. При помощи чисел даже можно описать настроение человека, например, по шкале от 1 до 10, где 1 — очень грустный, 10 — очень радостный. Собственно математика (как наука, изучающая числа) берет своё начало со счета, а уже далее используются буквенные выражения и параметры. Но начинается все именно со счета, точнее с устного счета. Без чисел было бы весьма затруднительно ввести градацию чего-либо, сложно было бы производить сравнения. Например, если бы не было меры массы тела в граммах, выражающейся конкретным числом грамм, то люди бы описывали предметы только как легкие, более легкие, тяжелые, очень тяжелые, чрезвычайно тяжелые и т. д. Это бы значительно затруднило общий прогресс и развитие человеческой цивилизации.

Виды чисел

Имеется большое количество различных видов чисел. От наиболее простых натуральных, известных каждому ребёнку, до весьма сложных и специфичных комплексных, изучаемых в специальных разделах математики, физики. Ниже приводятся определения различных чисел. Перед этим важно отметить, что все числа определённого вида образуют в совокупности множество таких чисел. Например, множество простых чисел. Строго говоря, понятия число и множество чисел — разные понятия. Также, если не оговорено противное, термины «числа» и «множество чисел» — будут являться синонимами.

• Натуральные числа — числа используемые при счете: 1, 2, 3, 4, … Это самые простые числа, которыми начинает пользоваться каждый ребёнок ещё в детском саду, осваивая технику устного счета до 10. Множество всех натуральных чисел обозначается обычно латинской буквой N.
• Целые числа — это натуральные числа, а также число 0, и все, противоположные натуральным (то есть со знаком минус) числа вида −1, −2, −3, …. Можно сказать, что множество целых чисел образуется как множество натуральных чисел, дополненное множеством натуральных чисел, взятых со знаком минус, а также числом 0. Очевидно, что целых чисел больше, чем натуральных чисел. Хотя, и тех и тех — бесконечное количество. Сразу сделаем оговорку, что сравнивать количество двух бесконечных множеств не так-то просто. Порой сравнение таких множеств требует специальных навыков и знаний из области высшей математики. Множество целых чисел обозначается буквой Z.

• Положительные числа — это любые числа, не только натуральные, большие нуля. Например, ${\sqrt {3}}$, 5,75 и т. п.
• Отрицательные числа — это любые числа, которых бесконечное множество, меньшие нуля. Необходимость введения отрицательных чисел появляется, чтобы, например, иметь возможность выражать температуру воздуха, когда на улице мороз. Также отрицательные числа начали употребляться на практике, когда нужно было говорить о денежном долге или недостаче, например, долг в 10 рублей удобно обозначить через −10 руб.
• Неотрицательные числа — это множество положительных чисел, а также число 0.
• Рациональные числа — числа, которые можно представить в виде обыкновенной дроби $m/n$, где m и n — целые, при этом n не равно 0. При этом множество рациональных чисел включает в себя множество целых чисел, так как любое целое число Z представляется в виде $Z/1$. Множество рациональных чисел обозначается символом Q.
• Десятичные дроби — это числа, которые можно записать в виде m/n, где n- степень числа 10, например, $3/100$ или $7/10000$. Для таких дробей существует десятичный вид записи. Для наших примеров это будет соответственно 0,03 и — 0,0007.
• Бесконечные периодические десятичные дроби — это дроби вида $0,33(3)$ или $0,25(25)$. Здесь в скобках записывается сам период. Важно отметить, что каждая такая дробь есть число рациональное. Например, периодической дроби $0,33(3)$ соответствует обыкновенная дробь $1/3$.
• Иррациональные числа — это действительные числа, которые не являются рациональными. Примером таких чисел могут быть бесконечные непериодические десятичные дроби. Например, дробь 0,1234567891011121314… где после запятой последовательно записываются все натуральные числа не является периодической и является иррациональным числом. Также на практике иррациональные числа появились, когда нужно было посчитать диагональ квадрата со стороной 1. По теореме Пифагора данная диагональ составляет ${\sqrt {2}}$, что не является рациональным числом. В самом деле, если предположить что ${\sqrt {2}}=m/n$ и дробь $m/n$ — несократимая, то возведя обе части равенства в квадрат получим $m^{2}=2*n^{2}$. Отсюда следует вывод, что m — четное число. Но тогда получим что и n- число четное, что противоречит несократимости исходной дроби. На самом деле любое число вида ${\sqrt {N}}$, где N — не является квадратом числа, является иррациональным.
• Действительные (или вещественные) числа — это множество рациональных и иррациональных чисел. Графически множество действительных числе представляется как числовая прямая. Множество действительных чисел обозначается буквой R. Сделаем важную оговорку, что до сих пор здесь выше по тексту обсуждались только действительные числа.
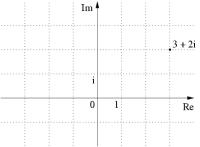
• Комплексные числа — числа вида $a+b*i$, где a, b — вещественные числа, i — мнимая единица, то есть число, квадрат которого дает минус единицу. Здесь принято называть a — действительная часть, b — мнимая часть комплексного числа. Графически множество комплексных числе представляет собой плоскость. Для того чтобы это представить, действительную часть (ее обозначают Re) числа можно откладывать по оси абсцисс, а мнимую часть (Im, от латинского imaginarius — мнимый)— по оси ординат. В этом представлении комплексные числа похожи на вектора на плоскости. На рисунке можно видеть комплексное число $3+2*i$.

изображение комплексных чисел на плоскости

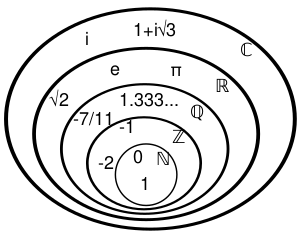
Для комплексных чисел также можно искать длину (или модуль) числа = ${\sqrt {a^{2}+b^{2}}}$. Легко видеть, что в случае $b=0$ получаем подмножество всех действительных чисел. Иными словами, каждое действительное число является комплексным числом с нулевой мнимой частью. Возникновение комплексных чисел связано, например, с необходимостью решений квадратных уравнений с отрицательным дискриминантом. Хоть комплексных чисел и бесконечное количество, все решает одно единственное число (мнимая единица) i. Комплексные числа нельзя сравнивать на больше меньше между собой, нельзя сравнивать с нулем. Можно лишь отдельно сравнивать мнимые и действительные части числа. Множество комплексных чисел обозначается символом C. Взаимосвязь перечисленных выше множеств чисел N, Z, Q, R, C представлена на рисунке 1.

• Проценты — это сотая часть числа, в переводе с латыни pro centum — «сотая часть». Говорят, когда-то у наборщика сломалась литера, в результате чего возник этот причудливый знак %, признанный затем во всем мире. Запись отношений стала удобнее, исчезли нуль и запятая, а символ % сразу указывает, что перед нами относительная величина, а не граммы, литры, рубли или метры. В наши дни процент часто рассматривают как специальную запись любого числа. Например, число 136 можно записать как 13600 %.
• Промилле — тысячная доля числа или 0,1 % какого-либо числа. Данный вид числа также носит относительный характер, как и проценты. Например, 0,003 составляет 3 промилле. Промилле обозначается специальным символом ‰ ;

символ для обозначения промилле

• Аликвотные дроби — это дроби вида $1/n$, где n — натуральное число. Название термина произошло от латинского «aliquot» — несколько. Древние египтяне именно таким дробям отдавали предпочтение, за исключением дроби $2/3$. Интересными задачами были представление какой-либо дроби в виде суммы аликвотных дробей. Например, $2/43=1/42+1/86+1/129+1/301$.
• Алгебраические числа — это числа, являющиеся корнями различных уравнений вида $a_{n}*x^{n}+...+a_{1}*x+a_{0}=0$, где $a_{i}$ — целые.
• Трансцендентные числа — действительные числа, не являющиеся алгебраическими. Сюда относятся, например, числа π и е.

Системы счислений. Десятичная и двоичная системы

В повседневной жизни нас окружают числа, состав которых записывается через цифры от 0 до 9. Иными словами, используемых цифр в записи числа всего десять. Поэтому общепринятая система счисления называется десятичной позиционной системой счисления. Она называется позиционной системой счисления, так как значение числа зависит от позиции цифр, используемых в нём (чем левее стоит цифра в записи числа, тем больше её вклад в величину числа). При этом 10 — в данной системе счисления является основанием. С другой стороны для понимания значимости числа 10 в данной системе счисления, приведем тот факт, что любое число можно разложить в сумму его разрядов, то есть по десяткам, сотням, тысячам и т. д. Например, число $2537=2*1000+5*100+3*10+7*1=2*10^{3}+5*10^{2}+3*10^{1}+7*10^{0}$. При этом цифры, используемые в записи исходного числа, будут коэффициентами в этом разложении. Данное разложение любого числа будет стандартным в десятичной позиционной системе счисления.

В то же время свое применение находят и другие системы счисления. Если в качестве основания системы счисления использовать не 10, а 2, то получится запись чисел уже в двоичной системе счисления. При этом цифрами в двоичной системе счисления будут только 0 и 1, а любое число будет записываться при помощи нулей и единиц. Например, число 1101 в двоичной системе будет $1*2^{3}+1*2^{2}+0*2^{1}+1*2^{0}=8+4+1=13$ в десятичной системе счисления. Получается, что число 13 в десятичной системе имеет 2 разряда для записи, а в двоичной системе целых 4 разряда, так как различных цифр для записи числе всего две. Использование двоичной системы счисления нашло свое применение в персональных компьютерах и вычислительной технике, где для данной ячейки ноль — это отсутствие сигнала, а 1 — его наличие. Вообще говоря можно использовать любое основание (целое положительное число, большее единицы) в качестве системы счисления. Алгоритм и логика остаются такими же. Весьма популярна также система счисления с основанием 12, где счет идет дюжинами.

Названия больших чисел

Самого большого числа не существует, но существует потребность называть большие числа именами. Например, единица с шестью нулями или 10^6 есть миллион, 10^9 есть миллиард. Хотя данных терминов можно было и не изобретать, а именовать миллион как тысяча тысяч. Миллиард можно наименовать как тысяча миллионов. Тем не менее существуют специальные названия для чисел вплоть до $10^{99}$. Также есть специальные отдельные числа, например, число $10^{100}$ — гугол, а 10 в степени гугол — гуголплекс. Ниже приведены названия на русском языке первых 14 больших чисел:

• $10^{3}$ — тысяча
• $10^{6}$ — миллион
• $10^{9}$ — миллиард, биллион
• $10^{12}$ — триллион
• $10^{15}$ — квадриллион
• $10^{18}$ — квинтиллион
• $10^{21}$ — секстиллион
• $10^{24}$ — септиллион
• $10^{27}$ — октиллион
• $10^{30}$ — нониллион
• $10^{33}$ — дециллион
• $10^{36}$ — ундециллион
• $10^{39}$ — дуодециллион
• $10^{42}$ — тредециллион

Простые числа

Здесь будем рассматривать только натуральные числа. Любое такое число делится нацело (то есть без остатка), как минимум, на единицу и на себя. Если же число делится ещё на какое-либо, то оно называется составным числом. В противном случае такое число называется простым числом. Например, число 18 делится нацело на 1, 18, 2, 3, 6 и 9. То есть 18 — число составное. Число 19 делится только на 1 и на 19, поэтому является простым. Для того чтобы ответить на вопрос является ли какое-либо число простым, нужно, в первую очередь, попробовать разложить данное число на множители, при этом 1 здесь не будет считаться множителем. Например, $15=3*5$, поэтому видно, что 15 не является простым числом. $45=9*5=3^{2}*5$.

Однако если число достаточно большое, например 1999, то сразу не получается его ни разложить на множители, ни доказать, что множителей таких не существует. На самом деле, чтобы доказать, что это число является простым, достаточно перебрать в качестве делителей не все числа вплоть до 1999, а лишь до 44. Это становится очевидным, если понять, что $44<{\sqrt {1999}}<45$. В самом деле, если существует делитель, то существует и пара делителей (исключая само число и единицу). При этом меньший делитель не должен превышать 45.

Простых чисел бесконечно много. Чтобы доказать данный факт можно использовать метод доказательства от противного. В самом деле, предположив, что есть максимальное простое число V, рассмотрим число А, равное произведению всех простых числе до V включительно и увеличенное на 1. То есть $A=2*3*5*7*...*V+1$. Число А будет и представлять простое число, большее V. В самом деле, оно не может быть составным, так как в своем разложении видно, что при делении на каждое простое число дает в остатке 1.

Специальные числа: Пи, e

Наиболее часто встречаются такие константы (то есть постоянные) как $\pi$, e. Эти два числа получили широкое применение в различных областях математики и физики и поэтому заслуживают отдельного внимания.

Торт с числом Пи

Число Пи — это отношение длины окружности к её диаметру. При этом такое отношение не зависит от размера самой окружности и постоянно для любых окружностей. Обозначение Пи появилось из первой буквы греческого слова «периферия» (окружность). Значение числа Пи выражается бесконечной и непериодической десятичной дробью, поэтому данное число является иррациональным. первые несколько знаков после запятой числа Пи выглядят так $3,141592653589...$ В наше время мощные современные компьютеры могут найти данное число с точностью до миллиона и более знаков после запятой. Однако в древности эти знаки приходилось находить на практике с помощью построений, например, вписывая и описывая в данную окружность правильные многоугольники и увеличивая число их сторон. В этом случае длина окружности была заключена между длинами описанного и вписанного многоугольника. Также значение числа Пи математики пытались найти, используя его разложение в виде бесконечных числовых рядов или произведений дробей. Например, Готфрид Вильгельм Лейбниц в 1674 г. установил следующую формулу: $\pi /4=1-1/3+1/5-1/7+...$. Однако данный ряд сходится очень медленно, поэтому на практике для нахождения точных знаков после запятой мало применим.

Число e выражается следующей бесконечной непериодической десятичной дробью 2,718281828459… Число е равно пределу числовой последовательности при неограниченном росте n, то есть $e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$ Обозначение e ввел Леонард Эйлер в 1736 году. Он также вычислил первые 23 знака этого числа.

Число $e$ иррациональное и трансцендентное. Доказательство трансцендентности впервые привел французский математики Шарль Эрмит в 1873 году. Также число е играет огромную роль в математическом анализе и теории функций. Если рассмотреть показательную функцию с основанием е (её называют экспонентной $e^{x}$, то у такой функции значение производной будет совпадать с самой функцией. $(e^{x})'=e^{x}$

Также если рассмотреть логарифм с основанием е, то такой логарифм будет называться натуральным логарифмом.

Признаки делимости

В различных прикладных задача очень полезно раскладывать исходное число на множители, а для этого нужно быть знакомым с признаками делимости.

• Признак делимости на 2. Число N делится на 2 тогда и только тогда, когда его последняя цифра делится на 2.
• Признак делимости на 4. Число N делится на 4 тогда и только тогда, если на 4 делится число, образованное из двух последних цифр числа N.
• Признак делимости на 8. Число N делится на 8 тогда и только тогда, если на 8 делится число, образованное из трех последних цифр числа N. Например, 1184 делится на 8, так как 184 делится нацело на 8.
• Признак делимости на 5. Число N делится на 5 тогда и только тогда, если его последняя цифра 0 или 5.
• Признак делимости на 3. Число N делится на 3 тогда и только тогда, если сумма его цифр делится на 3. Например, число 774 делится на 3, так как $7+7+4=18$ делится нацело на 3.
• Признак делимости на 9. Число N делится на 9 тогда и только тогда, если сумма его цифр делится на 9.
• Признак делимости на 11. Число N делится на 11 тогда и только тогда, если сумма его цифр, стоящих на нечетных местах, отличается от суммы его цифр, стоящих на четных местах, на величину, кратную 11. Например, 176 делится на 11, так как $7-7=0$ делится на 11.
• Признак делимости на 13. Число N делится на 13 тогда и только тогда, если на 13 делится число, полученное из исходного зачеркиванием последней цифры и прибавлением к полученному числу учетверенного значения этой цифры. Например, 143 делится на 13, так как $14+4*3=26$ делится нацело на 13.

Средние значения

В повседневной практике наиболее часто используется в качестве среднего значения (средний возраст, средняя цена и т. п.) «среднее арифметическое». Среднее арифметическое m для двух положительных чисел а и в составляет их полусумму, то есть на языке формул это записывается следующим образом: $m={\frac {a+b}{2}}$ Более редко используются следующие виды средних величин:

• среднее геометрическое $k={\sqrt {a*b}}$
• среднее гармоническое $p={\frac {2}{1/a+1/b}}$
• среднее квадратичное $d={\sqrt {\frac {a^{2}+b^{2}}{2}}}$

Средствами школьной элементарной математики доказывается, что выполняется следующее соотношение между вышеприведенными средними величинами:

$p\leqslant k\leqslant m\leqslant d$ При этом равенство возникает лишь тогда, когда $a=b$.

Литература

• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
• Якушева Е.В., Попов А.В.,Якушев А.Г. Математика все для экзамена. — М.: УНЦ ДО, 2004. — ISBN 5-88800-226-7.}
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Воробьёв Н. Н. Признаки делимости. — 4-е изд. — М.: Наука, 1988. — Т. 39. — 94 с. — (Популярные лекции по математике). — ISBN 5-02-013731-6.
• В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — ISBN 5-482-00445-7.

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!