Линейная алгебра

Наука
Математика
Тема	Линейная алгебра
Предмет изучения	векторные пространства и их подпространства, линейные отображения, линейные, билинейные и квадратичные функции
Основные направления	математика
Вспомогат. дисциплины	алгебра, геометрия, математический анализ, тригонометрия

Линейная алгебра — один из разделов алгебры, рассматривающий векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные и квадратичные функции (функционалы или формы) на векторных пространствах. Главные инструменты линейной алгебры – матрицы, детерминанты и двойственные пространства.

История

Древние цивилизации Вавилона и Египта, Греции

В «Арифметике» Диофанта (III век нашей эры) были обобщены:

• арифметические действия над множествами целых и рациональных неотрицательных чисел;
• в расчетах по геометрии и астрономии введено использование алгебраических формул;
• сформулированы задачи на построение/удвоение куба и трисекции угла.

Восточная цивилизация средних веков

В сочинение Мухаммад ибн Муса аль-Хорезми «Краткая книга об исчислении аль-джебры и аль-мукабалы» (примерно 825 год) посвящено ре­шению уравнений 1-й и 2-й сте­пе­ней и термин «алгебра» впер­вые рас­смат­ри­ва­ет­ся как са­мо­сто­ятельный раздел ма­те­ма­ти­ки.

Эпоха Возрождения, XV—XVI века

С. Дель Ферро, Н. Тарталья, Д. Кардано, Л. Феррари, Ф. Виет, Р. Бомбелли внесли вклад в решение общих алгебраических уравнений третьей и четвертой степени.

Была разработана современная алгебраическая символика, символическое обозначение коэффициентов и неизвестных в алгебраических выражениях, сформулирована основная теорема алгебры, согласно которой уравнение имеет столько корней, какова его степень.

XVII—XVIII века

Р. Декарт, П. Ферма, И. Ньютон, Г. Лейбниц, Л. Эйлер, Ж. Даламбер, Ж.-Л. Лагранж, Г. Крамер, П. Лаплас, А-Т. Вандермонд внесли вклад в:

• зарождение аналитической геометрии;
• развитие теории чисел;
• расширение теории алгебры многочленов;
• поиски общих формул для решения алгебраических уравнений;
• первые подходы к доказательству существования корня уравнения с числовыми коэффициентами;
• появление теории определителей.

XIX-начало XX века

К. Гаусс, П. Дирихле, Э. Куммер, Л. Кронекер, Р. Дедекинд, Е. Золотарев, Г. Вороной, А. Марков:

• была доказана основная теорема о существовании корней уравнений с целыми коэффициентами;
• получила интенсивное развитие теория алгебраических чисел.

П. Чебышёв, Ш. Эрмит, Н. Лобачевский, А. Гурвиц занимались:

• поиском методов приближенного решения алгебраических уравнений;
• определения условий коэффициентов, обеспечивающие заданное расположение корней.

П. Руффини, Н. Абель, К. Якоби, Э. Галуа, Б. Риман, О-Л. Коши, М. Жордан, П. Силов, работы которых посвящены:

• решению проблемы о неразрешимости общих уравнений степени, больших пяти в радикалах;
• развитию теории алгебраических функций;
• началам теории конечных групп, преимущественно на базе групп перестановок.

Г. Грассман, Д. Сильвестр, А. Кэли, Р. Гамильтон, Д. Буль, М. Ли, Ф. Фробениус, Ж. Серре, А. Нётер, Д. Граве, Ж. Пуанкаре, Ф. Клейн, У. Бёрнсайд, Ф. Молин, И. Шур, Г. Вейль, А. Энриквес занимались:

• активным развитием методов линейной алгебры;
• были открыты кватернионы;
• создана теория алгебр и групп Ли;
• алгебраической геометрией и теорией инвариантов.

Работы Д. Нейман, Д. Гильберт, Э. Картан, К. Гензель, Э. Штейниц, Э. Нётер, Э. Артин, Н. Бурбаки привели к

• полной перестройки всего здания математики;
• к переходу алгебры на более абстрактный и аксиоматический путь развития.

Начало-середина XX века

Н. Чеботарёв, О. Шмидт, А. Мальцев, А. Курош, С. Новиков, Л. Фаддеев и другие советские математике внесли свой вклад в ведение в обиход языка теории колец, модулей, категорий, гомологий. Многие разрозненные теории оказались уложены в общую схему универсальной алгебры, при этом на стыке алгебры и математической логики родилась теория моделей, получили яркие взлеты теории конечных групп.

• Математики - основоположники линейной алгебры
• 

  Диофант

• 

  Мухаммад ибн Муса аль-Хорезми

• 

  Тарталья

• 

  Кардано

• 

  Виет

• 

  Ньютон

Элементы линейной алгебры

Матрицы и определители

Матрица

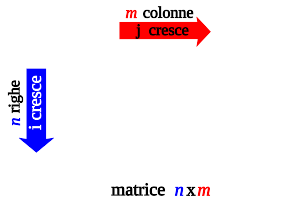
Матрица — это прямоугольная таблица, образованная из элементов некоторого множества и состоящая из m строк и n столбцов.

Виды матриц:

1. Квадратная матрица:
   • диагональная,
   • единичная,
   • нулевой,
   • верхняя треугольная,
   • нижняя треугольная.
2. Вектор:
   • вектор-столбец,
   • вектор-строка.

Линейное пространство

Линейное пространство

Множество векторов L с определенными на на нём операциями сложения векторов и умножения векторов на числа из поля K, не выводящие сумму векторов и произведение вектора на

число из множества L, называется линейным пространством, если справедливы следующие свойства:

I. задано правило сложения, ставящее в соответствие любым двум элементам a, b из V единственный элемент c из V , называемый суммой и обозначаемый c = a + b;

II. задано правило умножения на число, ставящее в соответствие каждому a из V и каждому α из F единственный элемент d из V , обозначаемый d = α · a или d = a · α; знак операции «·» часто опускают;

III. выполняются аксиомы линейного пространства.

Системы линейных уравнений

Алгебраической линейной системой m уравнений с n неизвестными называется система уравнений вида: ${\begin{cases}a_{11}x_{1}+a_{12}x_{2}+...+a_{1m}x_{n}=b_{1},\\a_{21}x_{1}+a_{22}x_{2}+...+a_{2m}x_{n}=b_{2},,\\...\\a_{n1}x_{1}+a_{n2}x_{2}+...+a_{mn}x_{n}=b_{m}\end{cases}}$

, где aij — коэффициенты системы; bi — свободные члены; xj — неизвестные значения

Евклидовы пространства

Векторное пространство V вместе с заданным на нем скалярным произведением называется евклидовым пространством

Линейные операторы

Если каждому вектору х из множества L по некоторому правилу (закону) поставлен в соответствие некоторый вектор y из множества M , то говорят, что на линейном пространстве L задан оператор Ā со значениями в пространстве M .

Билинейные и квадратичные формы

Билинейной функцией (или билинейной формой) на векторном пространстве V называется отображение α: V × V → K, линейное по каждому из двух своих аргументов.

Квадратичной функцией на векторном пространстве V называется функция q : V → K, для которой существует билинейная функция α: V × V → K такая, что q(v) = α(v, v) ∀ v ∈ V