Функция (математика)

Линейная функция

Фу́нкция — понятие в математике, означающее зависимость одних переменных величин от других. Величина понимается в самом широком смысле: именованное число, отвлечённое число (действительное или комплексное), несколько чисел (то есть точка пространства) и вообще элемент любого множества.

История возникновения функции

Понятие функции преодолело долгое развитие. Первое представление о функциональных зависимостях и их графических изображениях приведено в книге Пьера Ферма «Введение и изучение плоских и телесных мест» (1636), опубликованной в 1679. Исследование линий, а также их уравнения в «Геометрии» Р. Декарта (1637) свидетельствуют об ясном понимании взаимной зависимости между двумя переменными. Геометрическая форма, устанавливающая взаимосвязь действий интегрирования и дифференциации была приведена математиком из Лондона Исаака Барроу («Лекции по геометрии», 1670) . Понятием функции, имеющее геометрическую и механическую формы было обнаружено в трудах Исаака Ньютона. Однако термин «функция» изначально появился лишь в 1692 году у Г. В. Лейбница.. По мнению Лейбница, функции — различные точки, связанные с любой кривой, например, абсцисс её точки. Первое определение функции, похожее с современным по смыслу, встречается у Иоганна Бернулли (1718): «Функция — величина, состоящая из переменных и переменных». Основой определения является идея задачи функции с помощью аналитической формулы. Такая же идея проявляется и в определении Л.Эйлера, изложенном им в «Введении в анализ бесконечных» (1748): «Функция переменных является аналитическим выражением, которое составляется каким-то образом из переменных и числа или постоянного количества».

Способы задания функции

1. Аналитический. Функция задаётся с помощью математической формулы.

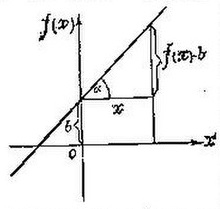
2. Графический. Задаётся функция графиком. Графический способ задания функции широко применяется на практике.

3. Табличный. Задаётся функция в виде таблицы, в которой различным значениям аргумента сопоставлены значения функций. Такой способ задания функции часто применяется тогда, когда область определения состоит из конечного числа значений.

4. Описательный способ. Функция задаётся словесным описанием, когда правило соответствия значений функции значениям аргумента выражено словами.

Основные свойства функций

1. Область определения функции

Область определения функции — мно­же­ст­во, на ко­то­ром за­да­на рас­смат­ри­вае­мая функ­ция, то есть со­во­куп­ность X всех элементов x, ка­ж­до­му из которых данная функция f ставит элемент y из не­ко­то­ро­го мно­же­ст­ва Y.

2.Область значений функции

Область значений функции — это множество значений, которые принимает зависимая переменная (переменная y). Обозначают область значений функции E(y).

3. Множество значений функции

Это множество всех действительных значений функции, которые она может принимать.

4. Нули функции

Точки, в которых функция или решение уравнения равняются нулю.

5. Четность (нечетность) функции

Функция — чётная, если все значения аргумента (x)

ƒ (-x)= ƒ (x). График четной функции симметрично относится к оси Оу.

Функция — нечётная, если все значения аргумента (x)

ƒ (-x)= — ƒ (x). График нечётной функции симметричен относительно начала координат.

6. Периодичность функции

Функция y=ƒ(x) называется периодической, если существует такое число T>0, что выполняется равенство ƒ (x)= ƒ (x±T). Число T называется периодом функции.

7. Возрастание и убывание функции

Если слева направо график функции «идёт вверх», то на этом промежутке функция возрастает, а если «вниз» — то убывает.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!