Тригонометрия

Наука
Математика
Тема	Тригонометрия
Предмет изучения	метрические соотношения между элементами треугольника
Период зарождения	термин впервые появился в 1595 году
Основные направления	математика
Вспомогат. дисциплины	алгебра, геометрия, математический анализ
Значительные учёные	Л. Эйлера, И. Кеплер, Н. Коперник, Т. Браге, Ф. Виет

Тригономе́трия (от греческого τρίγωνον — «треугольник» и «метрия»), раздел геометрии, в котором метрические соотношения между элементами треугольника описываются через тригонометрические функции, а также устанавливаются соотношения между тригонометрическими функциями. Первый раз термин появился в 1595 году в виде названия книги немецкого математика Бартоломеуса Питискуса (1561—1613).

Основные сведения

Тригонометрия изучается как в евклидовой, так и в неевклидовой геометрии. Тригонометрия сферы евклидова пространства называется сферической тригонометрией.

Тригонометрия в евклидовой геометрии

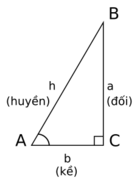
Тригонометрические функции в прямоугольном треугольнике

Прямоугольный треугольник

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника). Функции без приставки «ко» — основные тригонометрические функции, функции, содержащие приставку «ко» — дополнительные тригонометрические функции.

• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть углов от 0° до 90°. Углы 30⁰, 45⁰ и 60⁰ называют табличными, для нахождения значений других тригонометрических функций можно воспользоваться таблицами Брадиса или инженерным калькулятором.

Таблица значений для углов 30⁰, 45⁰ и 60⁰:

Угол α0	sinα	cosα	tgα	ctgα
300	${\frac {1}{2}}$	$${\frac {\sqrt {3}}{2}}$$	${\frac {1}{\sqrt {3}}}$	${\sqrt {3}}$
450	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {2}}{2}}$	1	1
600	${\frac {\sqrt {3}}{2}}$	${\frac {1}{2}}$	${\sqrt {3}}$	${\frac {1}{\sqrt {3}}}$

Тригонометрические функции в прямоугольном треугольнике связаны следующими формулами:

1. основное тригонометрическое тождество: $\sin ^{2}\alpha +\cos ^{2}\alpha =1$
2. ctg $\alpha$ * ctg$\beta$ = 1
3. cos $\alpha$ = sin$\beta$.

Тригонометрические функции в произвольном треугольнике

Произвольный треугольник

Решить произвольный треугольник, то есть по известным трем его элементам, найти остальные элементы треугольника, можно с использованием теоремы синусов и теоремы косинусов.

1. Теорема синусов ${\frac {a}{sin\alpha }}=$${\frac {b}{sin\beta }}$=${\frac {c}{sin\gamma }}$.
2. Теорема косинусов: $a^{2}=b^{2}+c^{2}-2cb\cos \alpha$, $b^{2}=a^{2}+c^{2}-2ac\cos \beta$, $c^{2}=a^{2}+b^{2}-2ab\cos \gamma$.

Тригонометрические функции и единичная окружность

Тригонометрические функции и единичная окружность

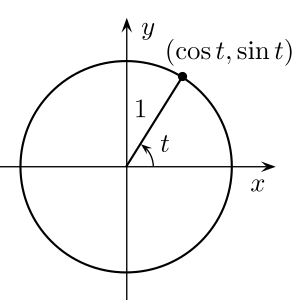
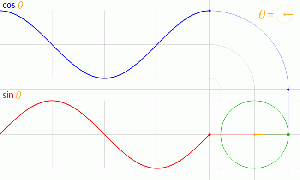
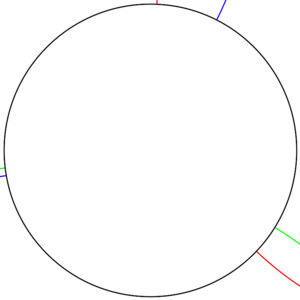
Тригонометрические функции и единичная окружность

Если точка лежит на тригонометрической окружности, а t — угол между осью абсцисс и радиус-вектором данной точки, отсчитываемый от положительного направления оси абсцисс, то её декартовы прямоугольные координаты (x, y) по определению равны

cos t и sin t соответственно.

cos t=x и sin t=y, остальные функции определяются как их отношения:

• тангенс — отношение синуса к косинусу,
• котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу),
• секанс — величина, обратная косинусу,
• косеканс — величина, обратная синусу.

Величина угла считается положительной, если отсчёт ведётся против часовой стрелки, и отрицательной, если отсчёт ведётся по ходу часовой стрелки.

Для тригонометрических функций произвольных углов справедливы следующие формулы:

1. основное тригонометрическое тождество: $\sin ^{2}\alpha +\cos ^{2}\alpha =1$
2. ctg $\alpha$ ctg$\beta$ = 1

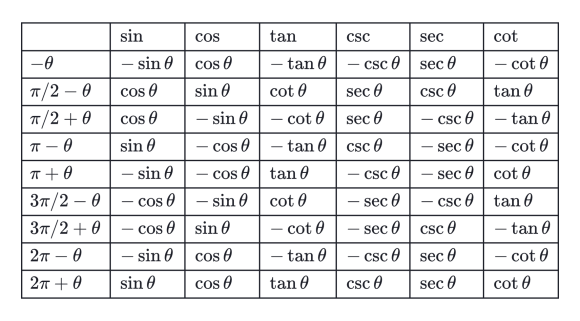
Для вычисления тригонометрических функций для углов, больших, чем острые, используют формулы приведения

Формулы приведения

Аналитическое определение

Синусоида и косинусоида

Тангенсоида

Каждому действительному числу x поставлены в соответствие числа sin x и cos x, а это значит, что на множестве R всех действительных чисел определены функции y = sin x и y = cosx — аналитическое определение. Тригонометрические функции синус, косинус, тангенс и котангенс относятся к основным элементарным функциям. Для графика функции синус используют название «синусоида», график функции косинус называют «косинусоида». График функции тангенс и котангенс — «тангенсоида», «котангенсоида» соответственно. Функции периодические, их графики имеют вид бесконечных волнообразных кривых. Секансоида и косекансоида — название графиков функций секанс и косеканс соответственно.

Сфери́ческий треугольник

Сферическая тригонометрия

Предмет сферической геометрии — решение сферических треугольников, образуемых на поверхности шара дугами больших кругов. А значит, сфери́ческая тригономе́трия, как раздел геометрии, изучает связи между углами и сторонами сферических треугольников. В сферическом треугольнике стороны a, b, c измеряются соответствующими центральными углами, а произведение этих углов и радиуса сферы — это длина его сторон. Используя, формулы сферической тригонометрии, можно по любым трём элементам сферического треугольника найти три его остальных элемента (решить треугольник).

Сферическая теорема Пифагора cos a = cos b cos d

Теорема косинусов для сферического треугольника:

• 1) cos a = cos b cos с + sin b sin с cos A;
• 2) cos A = sin B sin С cos a − cos B cos С.

Формулы пяти элементов:

• 1) sin a cos B = cos b sin с − sin b cos с cos A;
• 2) sin A cos b = cos B sin С + sin B cos С cos a

Теорема синусов для сферического треугольника: ${\frac {sinA}{sin\alpha }}=$${\frac {sinB}{sinb}}$=${\frac {sinC}{sinc}}$.

Тригонометрия в неевклидовой геометрии

Гиперболический треугольник, внутренние углы

В гиперболической геометрии сумма углов треугольника меньше 180⁰.

1. В треугольнике с прямым углом выполняются следующие соотношения:

• Гиперболический косинус гипотенузы c равен произведению гиперболических косинусов катетов a и b: ch c = ch a ch b (эту формулу называют гиперболической теоремой Пифагора);
• б) th a = sh b tg $\alpha$.

2. sh a = sh c sin $\alpha$, th b = th c cos $\alpha$, cos $\alpha$ = ch a sin$\beta$, ctg $\alpha$ ctg$\beta$ = ch c.

При малых a, b и c эти соотношения принимают вид: a = c sin $\alpha$, b = c cos $\alpha$, ctg $\alpha$ ctg$\beta$ = 1, cos $\alpha$ = sin$\beta$, то есть такие же как для функций в прямоугольном треугольнике евклидовой геометрии.

Для произвольного треугольника в гиперболической геометрии справедливы теоремы, аналогичные теоремам синусов и косинусов в евклидовой планиметрии.

История

Трактат по тригонометрии Ли Мадоу (китайское имя иезуита из Италии Маттео Риччи, 1552—1610 гг.)

Тригонометрия (от древне-греческого «треугольники измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 году как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).

Составление первых тригонометрических таблиц принадлежит Гиппарху Никейскому (180—125 лет до нашей эры). В его таблицах даны значения дуг и хорд для серии углов, соответствующие введённым позднее синусам.

Тригонометрия на плоскости начала развиваться позднее сферической, хотя отдельные её теоремы встречались и раньше. Например:

1) 12-я и 13-я теоремы 2-й книги «Начал» Евклида выражают по существу теорему косинусов.

2) Тригонометрия развивалась арабскими астрономами и математиками, которым была уже известна теорема синусов

• аль-Баттани (2-я половина IX — начало X веков)
• Абу-ль-Вефа (X век)
• Бхаскара (XII век)
• арабскими учёным Насиром ад-Дином ат-Туси (XIII век).

3) Теорема тангенсов была получена Региомонтаном (XV век).

4) Дальнейшие работы в области тригонометрии принадлежат

• Н. Копернику (1-я половина XVI век),
• Т. Браге (2-я половина XVI век),
• Ф. Виету (XVI век),
• И. Кеплеру (конец XVI — 1-я половина XVII веков).

Современный вид тригонометрия получила в работах Л. Эйлера (XVIII век).

Литература

1. Брадис В. М. Четырёхзначные математические таблицы: Для сред. шк. — 55-е изд. — М.: Просвещение, 1986. — 96 с.
2. Кранц П. Сферическая тригонометрия: пер. с нем./ под ред. Я. Н. Шпильерейна. Изд. 2-е. — М.: Издательство ЛКИ, 2007. — 96 с.
3. Прасолов В. В. Геометрия Лобачевского: Электронное издание — М.: МЦНМО, 2014 — 88 с
4. Иовлев Н. И. Введение в элементарную геометрию и тригонометрию Лобачевского.- Государственное издательство Москва, 1930 — 67 с.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!