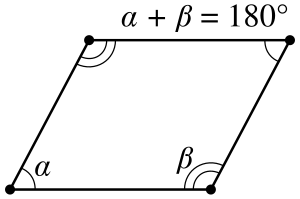Параллелограмм

Параллелогра́мм — это четырёхсторонняя геометрическая фигура, отличительной чертой которой служит попарная параллельность противолежащих сторон. Данные стороны располагаются на прямых линиях, которые никогда не пересекаются. Термин происходит от древнегреческих слов др.-греч. παράλληλος (параллельный) и др.-греч. γραμμή (линия).

Свойства параллелограмма

К специальным разновидностям данной фигуры относятся квадрат (одновременно прямоугольник и ромб), ромб (равенство всех сторон) и прямоугольник (прямые углы). Фигуру, которая не представляет собой ромб или прямоугольник, в геометрии именуют ромбоидом. В первой половине XX века в некоторых источниках термин «ромбоид» применялся для обозначения дельтоида. В алгоритмах компьютерной графики данная фигура служит обозначением операций ввода и вывода информации.

Основные характеристики

Противолежащие стороны имеют одинаковую длину, углы равны между собой. Два угла, расположенных рядом с одной стороной, дают в сумме 180° — такое свойство связано с тем, что противоположные стороны параллельны друг другу.

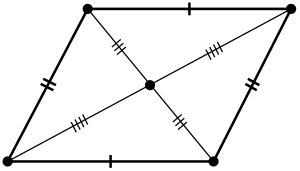
Диагонали встречаются в одной точке, которая находится точно посередине каждой диагонали. Эта точка является центром симметрии фигуры. Каждая диагональ делит фигуру на два треугольника одинакового размера. Средние линии также проходят через точку пересечения диагоналей, где все четыре отрезка разделяются на равные части.

Площадь параллелограмма

Длины сторон ($a$ и $b$) и высоты ($ha,hb$), опущенные к этим сторонам, связаны обратной зависимостью.

${\frac {a}{b}}={\frac {h_{b}}{h_{a}}}$

Существует важное правило (тождество) для параллелограмма: если сложить квадраты длин диагоналей, получится число, равное удвоенной сумме квадратов двух соседних сторон:

$d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2})$

где $a$ и $b$ — длины смежных сторон, а $d1$ и $d2$ — длины диагоналей.

Критерии определения

Четырёхугольник $\square ABCD$ классифицируется как параллелограмм при выполнении любого из перечисленных условий (остальные условия выполняются автоматически):

• диагонали делятся в точке пересечения пополам: $AO=OC$, $BO=OD$, где $O$ обозначает точку пересечения диагоналей;
• две противоположные стороны четырёхугольника без самопересечений одновременно равны и параллельны: $AB=CD,AB\parallel CD$;
• все противоположные стороны попарно параллельны: $AB\parallel CD,BC\parallel DA$;
• все противоположные углы попарно равны: $\angle A=\angle C,\angle B=\angle D$;
• все противоположные стороны четырёхугольника без самопересечений попарно равны: $AB=CD,BC=DA$;
• сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника:

$AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}$

• сумма средних линий выпуклого четырёхугольника равна его полупериметру.

Противоположные углы параллелограмма

Вычисление площади

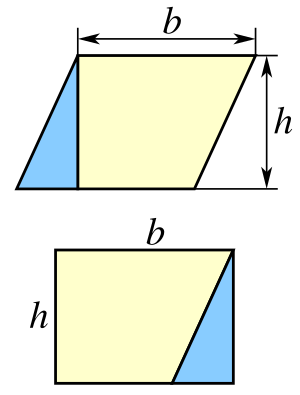
• Площадь фигуры определяется произведением основания на высоту:

$S=bh$, где $b$ представляет сторону, $h$ — высоту к данной стороне.

• Альтернативный способ расчёта использует длины смежных сторон и синус угла между ними:

$S=ab\sin \alpha$

• Третий метод определения площади применяет длины смежных сторон $a,b$ и длину произвольной диагонали $d$ по формуле Герона как сумму площадей двух одинаковых прилегающих треугольников:

$S=2\cdot {\sqrt {p(p-a)(p-b)(p-d)}}$

где $p=(a+b+d)/2$.

Литература

• Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.

Ссылки

• Weisstein, Eric W. Parallelogram (англ.) на сайте Wolfram MathWorld.