Треугольник
Треуго́льник — простейший многоугольник и одна из фундаментальных фигур евклидовой геометрии. Это часть плоскости, ограниченная тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой[1].
Основные элементы и классификация
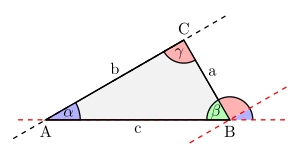
Вершины треугольника традиционно обозначают заглавными латинскими буквами A, B, C, а противолежащие им стороны — соответствующими строчными a, b, c. Три отрезка образуют в вершинах три внутренних угла; их сумма всегда равна 180°. Часть плоскости внутри сторон называют внутренностью треугольника — она учитывается, например, при вычислении площади[2][1].
Треугольники принято различать по двум ключевым критериям. В зависимости от величины наибольшего угла выделяют остроугольные треугольники, где все углы меньше 90°, прямоугольные — с одним углом ровно 90° (при этом стороны, образующие прямой угол, именуются катетами, а сторона, противолежащая прямому углу, — гипотенузой), а также тупоугольные, в которых один угол превышает 90°[3].
По числу равных сторон различают разносторонние треугольники, у которых все стороны имеют разную длину, равнобедренные — с двумя равными сторонами (их называют боковыми, а третью сторону — основанием), и равносторонние (или правильные) треугольники, в которых все три стороны равны между собой, а каждый из трёх углов составляет ровно 60°[3].
Важные линии и точки
В треугольнике выделяют несколько замечательных линий и точек их пересечения. Медиана представляет собой отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Все три медианы пересекаются в одной точке — центроиде, который также называют центром тяжести треугольника; при этом центроид делит каждую медиану в отношении 2 : 1, если считать от вершины[4][3].
Другой важной линией является высота — перпендикуляр, опущенный из вершины на прямую, содержащую противоположную сторону; три высоты треугольника (или их продолжения) пересекаются в общей точке, именуемой ортоцентром. Не менее значима биссектриса — отрезок, который идёт от вершины вдоль биссектрисы внутреннего угла до пересечения с противоположной стороной; три биссектрисы сходятся в одной точке, являющейся центром вписанной окружности. Кроме того, в треугольнике рассматривают серединный перпендикуляр — прямую, которая перпендикулярна стороне и проходит через её середину; три таких перпендикуляра пересекаются в точке, служащей центром описанной окружности. Наконец, средней линией называют отрезок, соединяющий середины двух сторон треугольника; она обладает важным свойством — параллельна третьей стороне и при этом равна её половине[3].
Основные свойства и теоремы
Неравенство треугольника: длина любой стороны меньше суммы длин двух других сторон (a<b+c и т. п.) и больше их разности. Теорема о сумме углов: сумма внутренних углов равна 180°[3].
Признаки равенства треугольников: треугольники равны, если у них соответственно равны: три стороны, две стороны и угол между ними, сторона и два прилежащих к ней угла. Признаки подобия треугольников: треугольники подобны, если три стороны одного пропорциональны трём сторонам другого, две стороны одного пропорциональны двум сторонам другого и углы между ними равны, два угла одного равны двум углам другого[1][3].
Теорема синусов: a/sinA=b/sinB=c/sinC=2R, где R — радиус описанной окружности. Формулы площади: S=1/2ah (по стороне а и высоте, проведенной к ней), S=1/2absinC (по двум сторонам и углу между ними), S= (формула Герона, где p=(a+b+c)/2 — полупериметр)[3].
Обобщения и приложения
Понятие треугольника допускает обобщения: в неевклидовой геометрии (например, на сфере) треугольник образуют три точки, соединённые геодезическими линиями. Вв n-мерной геометрии аналогом треугольника служит n-мерный симплекс[5][3].
Треугольники широко применяются в науке и технике: в геодезии и навигации (триангуляция), архитектуре и строительстве (жёсткие конструкции), компьютерной графике (моделирование поверхностей), физике и инженерии (расчёт сил и напряжений). Их свойства изучаются с древности, а многие теоремы о треугольниках (о средней линии, о пересечении медиан, о сумме углов и др.) входят в базовые курсы школьной геометрии[6][3].
Примечания
- ↑ 1,0 1,1 1,2 Треугольник. Большая российская энциклопедия (30 мая 2022). Дата обращения: 13 ноября 2025.
- ↑ Шевчук А. С. Треугольник — основные понятия, свойства и признаки. Понятная математика. Дата обращения: 16 ноября 2025.
- ↑ 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 Нигмедзянова А. М., Жукова С. А. Геометрия треугольника: учебно-методическое пособие / Нигмедзянова А. М., Жукова С. А.. — Казань: Казанский (Приволжский) федеральный университет, 2020. — С. 5—71. — 73 с.
- ↑ Батугин С. А. Неизвестные треугольники и бесконечность недоказанных теорем // Наука и техника в Якутии : журнал. — 2014. — № 2. — С. 112—113.
- ↑ Некрасов В. Л. Построение треугольников на сфере // Известия Томского политехнического университета. Инжиниринг георесурсов : журнал. — 1911. — № 4. — С. 1—19.
- ↑ Шлемов И. А., Гальянов А. В. Способы уравнивания треугольника // Известия Уральского государственного горного университета : журнал. — 2013. — № 3. — С. 43—46.
| Виды треугольников | |
|---|---|
| Замечательные линии в треугольнике | |
| Замечательные точки треугольника | |
| Основные теоремы | |
| Дополнительные теоремы | |
| Обобщения | |
