Теорема о внешнем угле треугольника

Теоре́ма о вне́шнем угле́ треуго́льника — одна из ключевых теорем в планиметрии. Теорема о внешнем угле треугольника, утверждающая, что он больше любого внутреннего угла, не смежного с ним, одна из основных теорем абсолютной геометрии. Она занимает центральное место в аксиоматической теории Гильберта и геометрии Лобачевского[1].

Внутренний и внешний углы треугольника

Определение

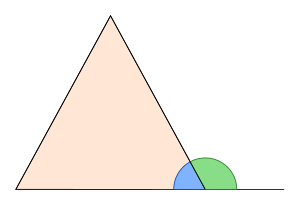
Внешний угол плоского треугольника при конкретной вершине — угол, который является смежным с внутренним углом этого треугольника при той же вершине[2]. Таким образом, внешний угол формируется стороной, исходящей из вершины, и продолжением другой стороны, выходящей из этой же вершины.

При каждой вершине треугольника можно построить по два внешних угла, продолжив одну или другую его сторону. Эти углы будут равны как вертикальные. У каждого треугольника три пары внешних углов. В отличие от внешних, углы самого треугольника называются внутренними[3].

Свойства внешнего угла

Внешний угол треугольника — это величина, получаемая путем вычитания градусной меры внутреннего угла, расположенного при той же вершине, из 180 градусов.

Градусная мера внешних углов может изменяться в диапазоне от 0 до 180 градусов, при этом крайние значения не включаются.

Биссектрисы внешнего и внутреннего углов любого треугольника всегда пересекаются под прямым углом[4].

Формулировка

Теорема абсолютной геометрии

Теорема о внешнем угле была впервые сформулирована и доказана древнегреческим математиком Евклидом в его знаменитом труде «Начала» (Предложение 16). Формулировка теоремы в переводе Дмитрия Дмитриевича Мордухай-Болтовского: «Во всяком треугольнике при продолжении одной из сторон внешний угол больше каждого из внутренних, <ему> противолежащих»[5].

Современный вариант формулировки — внешний угол треугольника больше любого несмежного с ним внутреннего угла этого треугольника[3].

Следствия

1. Из точки, не лежащей на прямой, можно провести один и только один перпендикуляр к этой прямой.

2. Если в треугольнике один из углов прямой или тупой, то два других угла острые[1].

Вторая формулировка теоремы о внешнем угле

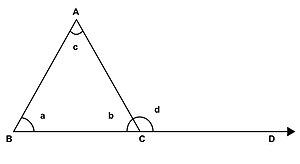
Внешний угол треугольника (рисунок 2)
Внешний угол треугольника (рисунок 1)

Словесная формулировка: внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных[6]. Например, если угол АCD является внешним углом треугольника, то он равен сумме углов ACB и BAC (рисунок 1)[7].

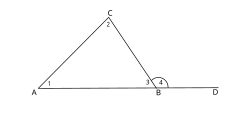
В математической форме: ∠4 = ∠1 + ∠2, где ∠4 — внешний угол, ∠1 и ∠2 — внутренние углы треугольника АВС (рисунок 2)[8].

Виды доказательств

Рассматривают два типа доказательств, с помощью которых можно убедиться в верности приведённого выше математического утверждения. Классическое доказательство теоремы о внешнем угле треугольника предложено Евклидом. В этом доказательстве используются свойства параллельных прямых[5][9]. Другое доказательство теоремы проводят с использованием теоремы о сумме углов треугольника и свойства смежных углов[8][10].

Примечания

  1. ↑ 1,0 1,1 Атанасян Л. С. Геометрия Лобачевского [Электронный ресурс]. — М.: БИНОМ. Лаборатория знаний, 2014. — С. 12—14. — 467 с. — ISBN 978-5-9963-2364-7.
  2. ↑ Внешний угол. Энциклопедический словарь (2009) Статьи на букву "В" (часть 44, "ВНЕ"-"ВНУ"). Дата обращения: 11 ноября 2025.
  3. ↑ 3,0 3,1 Киселёв А. П. Геометрия / Под ред. Н. А. Глаголева. — М.: ФИЗМАТЛИТ, 2004. — С. 39. — 328 с. — ISBN 5-9221-0367-9.
  4. ↑ Погорелов А. В. § 3. Признаки равенства треугольников // Элементарная геометрия: учеб. для 7—11 кл. сред. шк. / А. В. Погорелов.. — М.: Просвещение, 1990. — С. 44—47. — 383 с. — ISBN 5-09-002728-5.
  5. ↑ 5,0 5,1 Евклид. «Начала», Книга I, предложение 16 / перевод с греческого u комментарии А. Д. Мордухай-Болтовского. — Москва-Ленинград: Государственное издательство технико-теоретической литературы, 1950. — С. 29—30. — 450 с.
  6. ↑ Майсеня Л.И. Справочник по математике. Основные понятия и формулы. — Минск: Высшая школа, 2012. — С. 156. — 399 с. — ISBN 978-985-06-2035-4.
  7. ↑ Большая советская энциклопедия / гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1971. — С. 158. — 680 с.
  8. ↑ 8,0 8,1 Аверьянов Д. И. Математика: Большой справочник для школьников и поступающих в вузы. — М.: Дрофа, 1998. — С. 137. — 864 с. — ISBN 5-7107-2093-3.
  9. ↑ Прохоров Ю. В. Математический энциклопедический словарь / Главный редактор Ю. В. Прохоров. — М.: Советская энциклопедия, 1988. — С. 122. — 847 с.
  10. ↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. § 2.5 Свойства точек биссектрисы угла // Геометрия. 7—9 классы: учеб. для общеобразоват. учреждений / под научным руководством академика А. Н. Тихонова. — М.: Просвещение, 2023. — С. 71. — 417 с. — ISBN 978-5-09-102538-5.
Источник — https://znanierussia.ru/articles/index.php?title=Теорема_о_внешнем_угле_треугольника&oldid=2138341