Прямоугольный треугольник

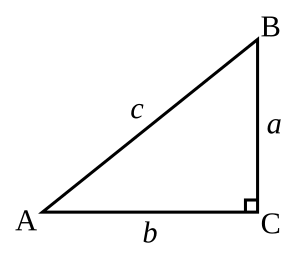
Прямоугольный треугольник

Прямоуго́льный треуго́льник — это треугольник, содержащий один угол величиной ровно 90° ($\pi /2$ радиан, что составляет четверть полного оборота). Данная геометрическая фигура является основой тригонометрии и используется в математических вычислениях. Свойство прямоугольного треугольника заключается в перпендикулярности двух его сторон, что позволяет рассматривать их как базис для системы координат.

Основные понятия

Определения и терминология

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади).

Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла. То есть как часть плоскости, ограниченную тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому исследование его свойств проводилось начиная с глубокой древности.

Каждый элемент прямоугольного треугольника имеет определённое название и специфические свойства. Наибольшая сторона, расположенная напротив прямого угла, называется гипотенузой (от греческого «гипотенуза» — натянутая). Термин происходит из древнегреческого языка и обозначает сторону, противоположную прямому углу. Гипотенуза обозначается буквой $c$ и является самой длинной стороной треугольника.

Две стороны, образующие прямой угол, называются катетами (от греческого «катетос» — отвес, перпендикуляр). Эти стороны обозначаются буквами $a$ и $b$. Каждый катет прямоугольного треугольника может быть рассмотрен как основание, при этом второй катет выступает в роли высоты, что упрощает вычисление площади треугольника.

Углы прямоугольного треугольника подчиняются определённому соотношению: прямой угол обозначается буквой $C$ и равен 90°, а два острых угла $A$ и $B$ в сумме составляют 90°. Это свойство называется комплементарностью углов, так как они дополняют друг друга до 90°. Например, если угол $A$ равен 30°, то угол $B$ составляет 60°.

Понятия «противолежащая сторона» и «прилежащая сторона» играют ключевую роль в тригонометрии. Для угла $A$ катет $a$ является противолежащим (находится напротив угла), а катет $b$ — прилежащим (примыкает к углу). Для угла $B$ ситуация обратная: катет $b$ противолежащий, катет $a$ прилежащий.

Связь с прямоугольниками

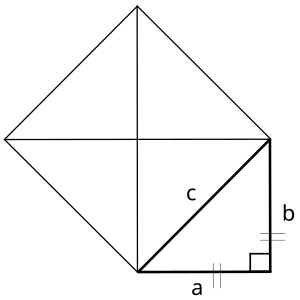
Прямоугольный треугольник соответствует половине прямоугольника, разделённого по диагонали. Эта связь определяет ряд свойств треугольника. Для прямоугольника со сторонами $a$ и $b$ длина диагонали равна ${\sqrt {a^{2}+b^{2}}}$, что соответствует длине гипотенузы треугольника.

При делении квадрата по диагонали образуется равнобедренный прямоугольный треугольник с равными катетами. Углы такого треугольника составляют 45°—45°—90°, что характеризуется осевой симметрией. Это свойство применяется в архитектуре при проектировании крыш, лестниц и декоративных элементов.

Пифагоровы треугольники

Пифагоровы треугольники характеризуются сторонами, выражаемыми целыми числами, что упрощает вычисления. В историческом контексте такие тройки применялись для построения прямых углов в строительстве без использования сложных измерительных инструментов.

Наиболее известная пифагорова тройка — 3, 4, 5. В Древнем Египте использовали верёвку с 12 узлами, разделённую на отрезки длиной 3, 4 и 5 единиц, для построения прямых углов при возведении храмов и пирамид. Это подтверждается вычислением:

$32+42=9+16=25=52$.

Другие распространённые пифагоровы тройки включают:

• 5—12—13, где $52+122=25+144=169=132$;
• 8—15—17, где $82+152=64+225=289=172$;
• 7—24—25, где $72+242=49+576=625=252$.

Существует бесконечное множество пифагоровых троек. Любую тройку можно получить умножением базовой на целое число. Например, от тройки 3—4—5 получаются 6—8—10, 9—12—15, 15—20—25 и так далее. Математики разработали формулы для генерации всех возможных пифагоровых троек.

Пифагорово утверждение

Фундаментальные соотношения

Теорема Пифагора

Теорема Пифагора является одной из самых известных и практически важных теорем математики. Она утверждает: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, что записывается формулой:

$a^{2}+b^{2}=c^{2}$

Геометрический смысл теоремы можно представить наглядно: если построить квадраты на каждой стороне прямоугольного треугольника, то площадь квадрата на гипотенузе будет равна сумме площадей квадратов на катетах. Теорема Пифагора выражает геометрическое соотношение, связывающее площади квадратов, построенных на сторонах прямоугольного треугольника.

Историки математики обнаружили более 400 различных доказательств этой теоремы. Одно из доказательств теоремы Пифагора предложил Джеймс Гарфилд в 1876 году, используя свойства трапеции. Древнекитайские математики применяли метод разложения площадей квадратов, а индийские — метод, основанный на подобии треугольников.

Обратная теорема не менее важна: если для треугольника со сторонами $a,b,c$ (где $c$ — наибольшая сторона) выполняется равенство $a^{2}+b^{2}=c^{2}$, то этот треугольник является прямоугольным. Это свойство используется в строительстве для проверки правильности углов без транспортира.

Теорема имеет множество обобщений. В трёхмерном пространстве действует теорема о диагонали прямоугольного параллелепипеда:

$d^{2}=a^{2}+b^{2}+c^{2}$

где $d$ — диагональ, $a,b,c$ — рёбра. В неевклидовых геометриях формула модифицируется в зависимости от кривизны пространства.

Тригонометрические соотношения углов

• Углы прямоугольного треугольника связаны системой тригонометрических соотношений, отражающих геометрические свойства фигуры. Поскольку один угол равен 90°, а сумма всех углов треугольника составляет 180°, два острых угла всегда дополняют друг друга: $A+B=90{\text{°}}$.

• Произведение косинусов всех трёх углов равно нулю: $\cos A\cdot \cos B\cdot \cos C=0$. Это происходит потому, что $\cos 90{\text{°}}=0$, и любое произведение с нулём даёт ноль. Данное свойство можно использовать как критерий прямоугольности треугольника.

• Сумма квадратов синусов всех углов в прямоугольном треугольнике равна двум: $\sin ^{2}{A}+\sin ^{2}{B}+\sin ^{2}{C}=2$. Учитывая, что $\sin 90{\text{°}}=1$, получаем $sin^{2}{A}+\sin ^{2}{B}+1=2$, откуда $\sin ^{2}{A}+\sin ^{2}{B}=1$. Это соотношение отражает основное тригонометрическое тождество для комплементарных углов.

• Аналогично, сумма квадратов косинусов равна единице: $\cos ^{2}{A}+\cos ^{2}{B}+\cos ^{2}{C}=1$. Поскольку $cos90{\text{°}}=0$, имеем $\cos ^{2}{A}+\cos ^{2}{B}=1$, что также следует из комплементарности углов.

• Соотношение для удвоенных углов выражается формулой: $\sin ^{2}{A}=\sin ^{2}{B}=2\sin A\cdot \sin B$. Это равенство отражает свойства острых углов прямоугольного треугольника и применяется в тригонометрических вычислениях.

Соотношения для сторон

Стороны прямоугольного треугольника связаны не только теоремой Пифагора, но и более сложными соотношениями, включающими радиусы окружностей. Сумма квадратов сторон прямоугольного треугольника связана с радиусом описанной окружности формулой:

$a^{2}+b^{2}+c^{2}=8R^{2}$.

Это соотношение можно понять через теорему Пифагора: $a^{2}+b^{2}=c^{2}$, следовательно, $a^{2}+b^{2}+c^{2}=2c^{2}$. Поскольку в прямоугольном треугольнике $R=c/2$, получаем $a^{2}+b^{2}+c^{2}=2c^{2}=8(c/2)^{2}=8R^{2}$.

Полупериметр $s=(a+b+c)/2$ прямоугольного треугольника связан с радиусами вписанной $r$ и описанной $R$ окружностей соотношением: $s=2R+r$. Это равенство характерно исключительно для прямоугольных треугольников.

Медиана прямого угла

Площадь и метрические характеристики

Вычисление площади

Площадь прямоугольного треугольника вычисляется несколькими способами, что демонстрирует разнообразие геометрических соотношений. Основная формула:

$S={\frac {1}{2}}ab$,

где $a$ и $b$ — катеты, следует из того, что треугольник составляет половину прямоугольника со сторонами $a$ и $b$.

Формула площади прямоугольного треугольника $S={\tfrac {1}{2}}ab$ является частным случаем общей формулы площади треугольника $S={\tfrac {1}{2}}\sin C$, так как в прямоугольном треугольнике $\sin 90{\text{°}}=1$.

Формула $S=r_{a}\cdot r_{b}=r\cdot r_{c}$ описывает соотношения между площадью прямоугольного треугольника и радиусами вневписанных окружностей. Здесь $r_{a},r_{b},r_{c}$ — радиусы вневписанных окружностей, касающихся сторон $a,b,c$ соответственно, а $r$ — радиус вписанной окружности.

Формула $S=r(2R+r)$ связывает площадь прямоугольного треугольника с радиусами вписанной и описанной окружностей, определяя площадь через эти параметры.

Формула через полупериметр $S=s(s-c)=((2s-c)^{2}-c^{2})/4$ демонстрирует связь между площадью и линейными размерами треугольника. Здесь $s$ — полупериметр, $c$ — гипотенуза.

Формула $S=\left|PA\right|\cdot \left|PB\right|$ использует точку касания $P$ вписанной окружности с гипотенузой $AB$. Отрезки $PA$ и $PB$ от точки касания до концов гипотенузы связаны с полупериметром: $\left|PA\right|=s-a,\left|PB\right|=s-b$. Подставляя эти выражения, получаем $S=(s-a)(s-b)$, что эквивалентно $S=s(s-c)$.

Периметр и его свойства

Периметр прямоугольного треугольника $P=a+b+c$ обладает свойствами, связанными с окружностями треугольника. Периметр прямоугольного треугольника равен сумме радиусов вписанной и всех трёх вневписанных окружностей:

$a+b+c=r+r_{a}+r_{b}+r_{c}$

Это соотношение не случайно. Радиус вписанной окружности равен $r=s-c$, радиусы вневписанных окружностей:

$r_{a}=s-a,\,r_{b}=s-b,\,r_{c}=s$

Складывая все четыре радиуса:

$r+r_{a}+r_{b}+r_{c}=(s-c)+(s-a)+(s-b)+s=4s-(a+b+c)=4s-2s$

Для периметра также справедлива оценка через неравенство треугольника. В прямоугольном треугольнике $c<a+b$ (гипотенуза меньше суммы катетов), но $c>\left|a-b\right|$ (гипотенуза больше разности катетов по модулю). Эти неравенства ограничивают возможные соотношения сторон.

Минимальный периметр при фиксированной площади достигается в равнобедренном прямоугольном треугольнике. Это свойство используется в задачах оптимизации, например, при проектировании конструкций с минимальным расходом материала.

Высоты и их свойства

Высота к гипотенузе

Высота, опущенная из вершины прямого угла на гипотенузу, определяет систему геометрических соотношений, используемых в различных приложениях. Эта высота $h$ не только делит исходный треугольник на два меньших, но и создаёт систему подобных фигур.

При опускании высоты на гипотенузу образуются три треугольника: исходный и два меньших. Все три треугольника подобны друг другу, что создаёт систему пропорциональных отрезков.

Высота $h$ является средним геометрическим между отрезками $d$ и $e$, на которые она делит гипотенузу:

$h^{2}=d\cdot e$

Геометрический смысл этого соотношения в том, что прямоугольник со сторонами $d$ и $e$ имеет ту же площадь, что и квадрат со стороной $h$.

Каждый катет представляет среднее геометрическое между гипотенузой и своей проекцией на неё. Для катета $a$:

$a^{2}=c\cdot d$ ,

где $d$ — проекция катета $a$ на гипотенузу $c$.

Аналогично для катета $b$:

$b^{2}=c\cdot e$

Эти формулы называются теоремами о катете.

Высота к гипотенузе выражается формулой:

$h={\frac {ab}{c}}$,

где $a$ и $b$ — катеты, $c$ — гипотенуза.

Эту формулу можно получить из равенства площадей: $S={\tfrac {1}{2}}ab={\tfrac {1}{2}}ch$, откуда $h={\tfrac {ab}{c}}$. Таким образом, высота к гипотенузе связывает все стороны треугольника в единое соотношение.

Связи высоты с катетами

Высота к гипотенузе связана с катетами фундаментальным обратным квадратичным соотношением:

${\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{f^{2}}}$

Это соотношение имеет физическую аналогию с законом сложения сопротивлений в электрических цепях при параллельном соединении. Алгебраически это соотношение можно вывести из формулы:

$f={\frac {ab}{c}}$

и теоремы Пифагора. Имеем:

$h^{2}={\frac {a^{2}b^{2}}{c^{2}}}={\frac {a^{2}b^{2}}{a^{2}+b^{2}}}$

Обращая это выражение:

${\frac {1}{h^{2}}}={\frac {a^{2}+b^{2}}{a^{2}b^{2}}}={\frac {1}{b^{2}}}+{\frac {1}{a^{2}}}$

Отрезки $d$ и $e$, на которые высота делит гипотенузу, связаны с катетами соотношениями

$d={\frac {a^{2}}{c}},\,e={\frac {b^{2}}{c}}$

Отношение этих отрезков равно отношению квадратов соответствующих катетов:

${\frac {d}{e}}={\frac {a^{2}c}{b^{2}c}}={\frac {a^{2}}{b^{2}}}$

Высота делит гипотенузу в отношении, равном отношению квадратов катетов. Для треугольника со сторонами $3,4,5$ высота делит гипотенузу на отрезки длиной 9/5 = 1,8 и 16/5 = 3,2, что соответствует отношению $32:42=9:16$.

Высоты от катетов

В прямоугольном треугольнике высоты, опущенные из концов гипотенузы на противоположные катеты, совпадают с самими катетами. Это происходит потому, что катеты перпендикулярны друг другу по определению прямоугольного треугольника.

Такая особенность делает вершину прямого угла ортоцентром треугольника — точкой пересечения всех трёх высот. В общем случае ортоцентр может находиться внутри, вне или на стороне треугольника, но в прямоугольном треугольнике он всегда совпадает с вершиной прямого угла.

Длины высот к катетам легко вычисляются. Высота к катету $a$ равна:

$h_{a}={\frac {bc}{a}}$

высота к катету $b$ равна:

$h_{b}={\frac {ac}{b}}$

Эти формулы получаются из равенства площадей треугольника при различных способах её вычисления.

Медианы

Медиана к гипотенузе

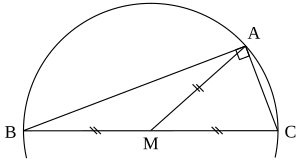
Медиана, проведённая от вершины прямого угла к середине гипотенузы, характеризуется свойством, специфичным для прямоугольных треугольников: она равна половине гипотенузы. Это выражается формулой:

$m_{c}={\frac {c}{2}}$ ,

где $m_{c}$ — медиана к гипотенузе, $c$ — длина гипотенузы.

Это свойство связано с теоремой Фалеса и свойствами описанной окружности. Поскольку центр описанной окружности прямоугольного треугольника находится в середине гипотенузы, медиана к гипотенузе является радиусом этой окружности.

Геометрически это означает, что вершина прямого угла находится на равном расстоянии от обеих вершин гипотенузы. Медиана к гипотенузе делит треугольник на два равнобедренных треугольника, каждый из которых имеет основание, равное половине гипотенузы, и равные боковые стороны длиной $c/2$.

Свойство медианы к гипотенузе применяется в конструировании для определения середины отрезка. Для нахождения середины отрезка, недоступного для прямого измерения, строится прямоугольный треугольник, где данный отрезок является гипотенузой, и измеряются расстояния от вершины прямого угла до концов гипотенузы. Равенство этих расстояний указывает на середину отрезка.

Соотношения между медианами

Медианы прямоугольного треугольника связаны системой алгебраических соотношений, отражающих особую геометрию этой фигуры. Основное соотношение:

$m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\tfrac {5}{4}}c^{2}$

где $ma$ и $mb$ — медианы к катетам, $mc$ — медиана к гипотенузе. Это соотношение можно вывести через координатную геометрию. Поместив треугольник в систему координат с вершинами $A(0,0)$, $B(a,0)$, $C(0,b)$, можно вычислить медианы по формуле расстояния между точками.

Медиана к катету $a$:

$m_{a}={\frac {1}{2}}{\sqrt {4b^{2}+a^{2}}}$

Медиана к катету $b$:

$m_{b}={\frac {1}{2}}{\sqrt {4a^{2}+b^{2}}}$

медиана к гипотенузе:

$m_{c}={\frac {1}{2}}{\sqrt {a^{2}+b^{2}}}={\frac {c}{2}}$

Подставляя в основное соотношение:

${\frac {1}{4}}(4b^{2}+a^{2}+4a^{2}+b^{2})={\frac {5}{4}}(a^{2}+b^{2})$

получаем:

${\frac {1}{4}}(5a^{2}+5b^{2})={\frac {5}{4}}(a^{2}+b^{2})$

Соотношение выполняется тождественно.

Сумма квадратов всех медиан связана с радиусом описанной окружности формулой:

$m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=6R^{2}$

Поскольку $R=c/2$, получаем:

$m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=6\left({\frac {c}{2}}\right)^{2}={\frac {3c^{2}}{2}}$

Медианы от катетов связаны с размерами треугольника более сложным соотношением:

$4c^{4}+9a^{2}b^{2}=16m_{a}^{2}m_{b}^{2}$

Это соотношение демонстрирует нелинейные связи в геометрии треугольника и используется в задачах на экстремум.

Ссылки

• Advanced right triangle calculator Right triangle calculator