Система координат
Систе́ма координа́т — набор математических правил, устанавливающих точкам пространства соответствующие значения координат[1]. С помощью системы координат можно описать положение точки, указав её координаты — числа, решать уравнения графическим способом, а так же находить длины, площади и объёмы различных предметов в пространстве. Система координат широко изучается школьниками на уроках математики, студентами в университетах различных профилей, а так же активно используется в различных науках.
История возникновения системы координат
Идея применения координатного метода возникла ещё в древнем мире. Древнегреческого ученого Анаксимандра Милетского (610-546 до н. э.) считают составителем первой географической карты. Он чётко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до н. э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определённых пунктов на поверхности Земли, при составлении календаря, звёздных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту[2].
Основные виды систем координат
Прямоугольная декартова система координат
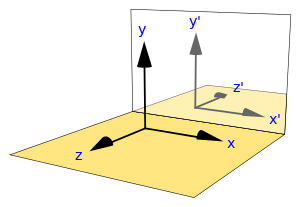
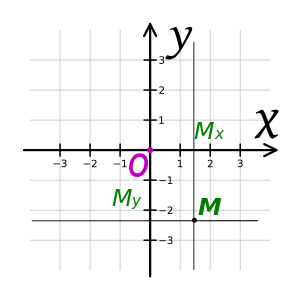
Взаимно перпендикулярные прямые с заданным положительным направлением и единичным отрезком, одинаковым для обеих прямых, называются осями координат. Точка пересечения осей координат называется началом координат и обозначается буквой О. Обычно ось координат, расположенную горизонтально и направленную вправо, принято называть осью абсцисс или осью Ох, а ось, расположенную вертикально и направленную вверх, называют осью ординат или осью Оу. Всю систему координат обозначают Оху, а плоскость, в которой она расположена, называют координатной плоскостью. Рассмотрим произвольную точку М плоскости Оху. Проведём через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел х, у по следующему правилу: х — координата точки М по оси Ох, у — координата точки М по оси Оу. Числа х и у называются прямоугольными декартовыми координатами точки М; при этом х называется ее абсциссой, а у — ординатой[3].
Координатные оси разбивают плоскость на четыре части, называемые координатными четвертями (квадрантами) или координатными углами. Эти квадранты нумеруются следующим образом: в направлении против хода часовой стрелки, начиная с того квадранта, где обе координаты положительные. Если на плоскости задана прямоугольная система координат Оху, то:
1) каждой точке на плоскости поставлена в соответствие упорядоченная пара чисел (пара координат точки);
2) разным точкам плоскости поставлены в соответствие разные упорядоченные пары чисел;
3) каждая упорядоченная пара чисел соответствует одной точке плоскости[3].
Полярная система координат
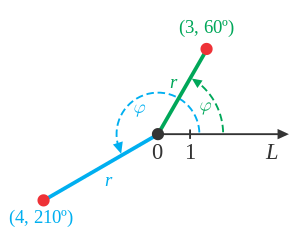
Полярными координатами точки М на плоскости (не совпадающей с полюсом) называют полярный радиус ρ = ОМ точки М и полярный угол φ, то есть угол, на который надо повернуть полярную ось против часовой стрелки до совпадения её с вектором OM (φ > 0 — поворот против часовой стрелки, φ < 0 — по часовой стрелке). Пара (ρ, φ) — координаты точки М в полярной системе координат. Положение любой точки М на плоскости однозначно определяется координатами ρ и φ, причем 0 ≤ ρ < ∞, 0 ≤ φ < 2π.
Если точка М совпадает с полюсом О, то ее полярный радиус ρ = 0, а угол φ можно выбрать любым. Обобщёнными полярными координатами точки М называют её полярные координаты ρ и φ такие, что - ∞ < ρ < ∞, — ∞ < φ < ∞. Чтобы указать точку М (ρ, φ) в обобщённой полярной системе координат, надо построить луч, образующий с полярной осью угол φ, затем отложить ρ единиц масштаба на нем, если ρ > 0, и на его продолжение, если ρ < 0[3].
Цилиндрическая система координат
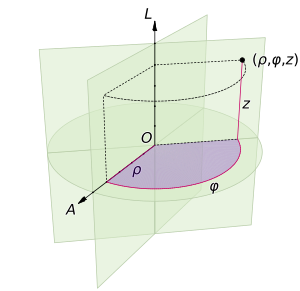
Трёхмерная система координат, расширяющая полярную систему добавлением третьей координаты, задающей высоту точки над плоскостью. Координатные линии — кривые, которые пробегает точка в случае, если две координаты зафиксированы, а третья варьируется. z — 1-ая координатная линия, окружность — 2-ая координатная линия, 3-я координатная линия проходит через точку P и параллельно оси Oz. Далее необходимо ввести орты (единичные вектора, которые являются касательными к координатным линиям и направлены в сторону возрастания координаты) цилиндрической системы координаты[4].
Сферическая система координат
Сфера — замкнутая поверхность, с множеством точек, равноудаленных от центра. Сферическая система координат образуется путём совмещения центра сферы с началом декартовой прямоугольной системы координат в пространстве, и уравнение сферы имеет следующий вид: х2 + у2 + z2 = ρ2 , где ρ — радиус сферы; x, y, z — координаты точки М.
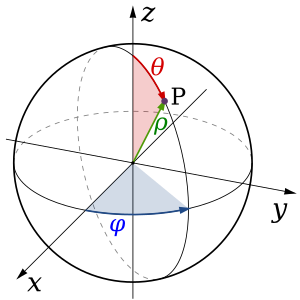
Начало координат в Сферической системе координат задано O. Сферическими координатами точки М являются три числа:
- ρ — расстояние от начала координат до точки М (0 ≤ ρ < + ∞);
- θ — угол между координатной осью Z и отрезком, соединяющим начало координат О с точкой М (0 ≤ θ ≤ 180º);
- φ — угол между координатной осью Х и проекцией отрезка ОМ на плоскость ХУ (0 ≤ φ < 360º)[5].
Применение системы координат в современном образовательном пространстве
Системы координат, будучи фундаментальным инструментом научных исследований, оказывают влияние на широкий спектр научных дисциплин. От астрономии, где они необходимы для точного определения положения космических объектов, до физики, где они помогают разгадывать сложные явления в микро- и макромирах. Использование систем координат в современной науке выходит за рамки простого описания положения объектов. Оно включает в себя анализ и понимание фундаментальных процессов, происходящих во Вселенной. Пример исследования гравитационных волн демонстрирует, как эти системы могут помочь в раскрытии новых научных горизонтов и глубоком понимании природы[6].
Примечания
- ↑ Афонин В. Ф. Высшая геодезия. Системы координат и преобразования между ними. — Новосибирск: СГУГиТ, 2020. — С. 8. — 112 с. — ISBN 978-5-907320-08-6.
- ↑ Бақытгүл Сатканова. Координаты в нашей жизни // Ұлы Дала Ұстазы. — № 000501.
- ↑ 3,0 3,1 3,2 Болотина Н. А., Харитонов Л. П., Руденок И. П. Высшая математика учебно-практическое пособие. — Волгоград, 2012. — С. 38,39. — 319 с. — ISBN 978-5-98276-487-4.
- ↑ Зобова А. А. Теоретическая механика. Часть 1. — МехМат МГУ. — С. 8. — 118 с.
- ↑ Клепко В. Л., Александров А. В. Системы координат в геодезии. — Екатеринбург: Министерство образования и науки Российской Федерации, 2011. — С. 13—14. — 116 с.
- ↑ Какалыев Б. А., Овезова Г. Ч. Применение систем координат в современной науке // Молодой учёный. — 2023. — Т. 49, № 496. — С. 11-12. — ISSN 2077-8295.
Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело! |
Данная статья имеет статус «проверенной». Это говорит о том, что статья была проверена экспертом |