Равнобедренный треугольник

Равнобедренный треугольник

Равнобе́дренный треуго́льник — геометрическая фигура, характеризующаяся наличием двух сторон одинаковой длины. Современная математическая интерпретация рассматривает такие треугольники как частный случай более общего определения, включающего фигуры с как минимум двумя равными сторонами.

Определения

Классификация

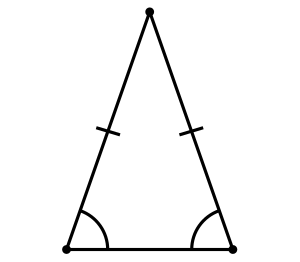
Треугольник является равнобедренным, если он обладает парой сторон равной длины. Эти одинаковые стороны принято называть боковыми, в то время как третья сторона получила название основания. Исторически Евклид формулировал определение более строго, требуя точного равенства только двух сторон.

Элементы

Равнобедренный треугольник АВС

Угол, формируемый пересечением боковых сторон, носит название вершинного. Противоположные ему углы, примыкающие к основанию фигуры, называются углами при основании и обладают особыми свойствами.

Симметрия

Осевая симметрия

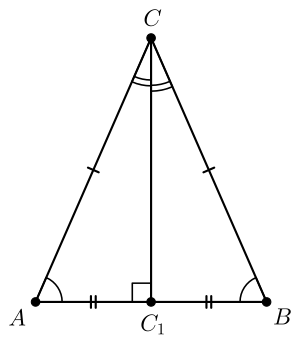
Равнобедренный треугольник характеризуется наличием единственной оси симметрии, проходящей через вершинный угол и центр основания. Данная ось одновременно представляет собой биссектрису вершинного угла, медиану к основанию, высоту из вершины и серединный перпендикуляр к основанию.

Особые точки

Центры вписанной и описанной окружностей располагаются на оси симметрии треугольника. Биссектрисы, высоты, медианы, проведённые из углов при основании, попарно равны между собой.

Вычисления

Соотношения сторон

Между элементами треугольника существует система взаимосвязей, где $a$ — длина боковой стороны, $b$ — длина основания, $\alpha$ — половина вершинного угла, $\beta$ — угол при основании:

$a={\frac {b}{2\cos \alpha }}$

$a^{2}=2Rh$

$b=a{\sqrt {2(1-\cos \beta )}}$

$b=2a\sin {\frac {\beta }{2}}$

$b=2a\cos \alpha$

Вычисление углов

Для определения углов используются различные подходы. Основные соотношения между углами:

$\alpha ={\frac {\pi -\beta }{2}}$

$\beta =\pi -2\alpha$

$\alpha =\arcsin {\frac {a}{2R}},\beta =\arcsin {\frac {b}{2R}}$

где $\alpha$ — половина вершинного угла, $\beta$ — угол при основании, $R$ — радиус описанной окружности.

Альтернативный метод не требует использования числа $\pi$ и радиуса описанной окружности:

$y=\cos \alpha ={\frac {b}{c}},\arccos y=x$

Радиусы окружностей

Радиус вписанной окружности может быть выражен несколькими способами в зависимости от известных параметров:

$r={\frac {b}{2}}{\sqrt {\frac {2a-b}{2a+b}}}$

$r={\frac {bh}{b+{\sqrt {4h^{2}+b^{2}}}}}$

$r={\frac {h}{1+{\frac {a}{\sqrt {a^{2}-h^{2}}}}}}$

$r={\frac {b}{2}}\operatorname {tg} \left({\frac {\alpha }{2}}\right)$

$r=a\cdot \cos(\alpha )\cdot \operatorname {tg} \left({\frac {\alpha }{2}}\right)$

Для описанной окружности справедливо соотношение

$a^{2}=2Rh$

где $R$ — радиус описанной окружности, $h$ — высота к основанию.

Периметр и площадь

Периметр равнобедренного треугольника вычисляется по формулам:

$P=2a+b$

$P=2R(2\sin \alpha +\sin \beta )$

Площадь может быть найдена различными способами:

$P=2R(2\sin \alpha +\sin \beta )$

$S={\frac {1}{2}}a^{2}\sin \beta ={\frac {1}{2}}ab\sin \alpha ={\frac {b^{2}}{4\tan {\frac {\beta }{2}}}}$

$S={\frac {1}{2}}b{\sqrt {\left(a+{\frac {1}{2}}b\right)\left(a-{\frac {1}{2}}b\right)}}$

Теоремы

Признак равнобедренности

Важным признаком равнобедренности служит теорема, доказанная в XIX веке: если в треугольнике две биссектрисы имеют одинаковую длину, то такой треугольник является равнобедренным. Данное утверждение было установлено математиками Лемусом и Штейнером в результате многолетней переписки.

Равносторонний треугольник представляет собой частный случай равнобедренного, но обратное утверждение является неверным.

История изучения

Математическое исследование равнобедренных треугольников имеет древние корни. Практики древнеегипетской и вавилонской математики владели методами вычисления площади таких фигур задолго до формального изучения их свойств древнегреческими математиками. Основополагающая теорема о равенстве углов при основании была сформулирована Евклидом как предложение I.5 и получила название «мост ослов» из‑за сложности её доказательства для начинающих изучать геометрию.

Литература

• Атанасян Л. С. Геометрия. 7—9 классы. — М.: Просвещение, 2019.
• Берже М. Геометрия. — М.: Мир, 1984. — Т. 1. — С. 340. — 560 с.
• Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — С. 336. — 509 с. — ISBN 5-17-009554-6.
• Киселёв А. П. Геометрия : планиметрия, стереометрия / под ред. Н. А. Глаголева. — М.: Физматлит, 2004. — 325 с. — ISBN 5-9221-0367-9.
• Погорелов А. В. Геометрия. 7—9 классы. — 6-е изд. — М.: Просвещение, 2018. — 239 с. — ISBN 978-5-09-059079-2.