Медиана треугольника

Медианы и центроид треугольника

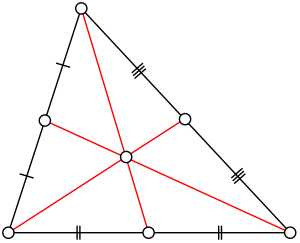
Медиа́на треуго́льника (лат. mediāna — средняя) — отрезок, который соединяет любую вершину треугольника с центральной точкой противолежащей стороны. Данный геометрический элемент играет фундаментальную роль в планиметрии, поскольку каждый треугольник обладает в точности тремя такими отрезками. Все медианы неизбежно пересекаются в единственной точке, которая называется центроидом и обладает уникальными физическими свойствами.

Этимология и терминология

Термин «медиана» происходит от латинского слова лат. mediāna, что означает «средняя». Это название отражает основную характеристику данного отрезка — его способность делить противоположную сторону пополам. В современной геометрии медиана может обозначать как сам отрезок, так и прямую, которая его содержит, а в некоторых контекстах — численное значение его длины.

В различных математических школах и традициях медианы обозначаются по-разному. Наиболее распространённой является система обозначений $m_{a},\ m_{b},\ m_{c}$ для медиан, проведённых соответственно к сторонам $a,b,c$ треугольника. Некоторые авторы используют обозначения $ma,mb,mc$ или даже специальные символы для подчёркивания направления медианы.

Точка пересечения медианы со стороной треугольника называется основанием медианы. Центроид делит каждую медиану на два сегмента с различными названиями: отрезок от вершины до центроида именуется предмедианой, а участок от центроида до основания — постмедианой. Эта терминология, введённая относительно недавно, помогает точнее описывать свойства различных частей медианы и их взаимные отношения.

Базовые свойства и центроид

Точка концентрации

Центроид треугольника представляет собой физический центр масс плоской фигуры с однородной плотностью. Это означает, что треугольная пластина будет находиться в равновесии, если её подпереть именно в этой точке. Центроид обладает замечательным свойством: он располагается на каждой медиане таким образом, что расстояние от него до вершины в два раза превышает расстояние до основания медианы.

Отношение предмедианы к постмедиане составляет строго 2:1 для любого треугольника, независимо от его формы или размера. Это фундаментальное свойство делает центроид уникальной точкой среди всех возможных точек пересечения различных линий треугольника.

Универсальность свойств

Каждая медиана выполняет функцию разделителя треугольника на две части равной площади. Это свойство остаётся неизменным для треугольников любой конфигурации — от остроугольных до тупоугольных. При этом важно понимать, что равенство площадей не гарантирует равенство форм получающихся частей.

Примечательно, что медиана является единственной линией треугольника, которая гарантированно делит его площадь пополам независимо от формы треугольника. Другие замечательные линии, такие как высоты или биссектрисы, не обладают этим универсальным свойством.

Совокупность всех трёх медиан создаёт внутри треугольника систему из шести меньших треугольников, каждый из которых имеет одинаковую площадь. Это разбиение обладает дополнительными геометрическими свойствами, которые находят применение в различных областях математики.

Свойства площади

Принцип равновеликого деления

Способность медианы делить треугольник на равновеликие части является одним из наиболее практически значимых свойств. В отличие от других линий треугольника, медиана гарантированно создаёт два треугольника с равными площадями, что делает её незаменимым инструментом в задачах на вычисление площадей и в доказательствах геометрических теорем.

Это свойство сохраняется даже при деформации треугольника, что подчёркивает его фундаментальный характер. Медиана также делит пополам любой отрезок, параллельный стороне, к которой она проведена.

Деление треугольника на части

Система трёх медиан формирует уникальную структуру внутри треугольника. Центроид становится общей вершиной для шести треугольников, три из которых примыкают к сторонам исходного треугольника, а три других — к его вершинам. Все эти шесть частей имеют равную площадь, составляющую одну шестую от площади исходного треугольника.

Каждый из шести треугольников может быть сопоставлен с определённым элементом исходного треугольника: либо с одной из его сторон, либо с одной из его вершин. Такое соответствие создаёт дуальную структуру, которая находит применение в алгебраической топологии и теории графов.

Интересным фактом является то, что если из длин медиан любого треугольника построить новый треугольник, его площадь будет составлять ровно три четверти от площади исходной фигуры. Это соотношение связано с глубокими метрическими свойствами евклидовой геометрии. Более того, длины медиан всегда удовлетворяют неравенству треугольника, что гарантирует возможность построения такого треугольника медиан.

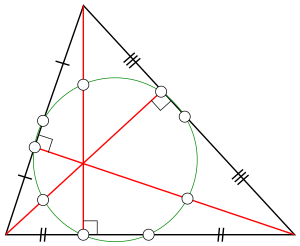
Центры описанных окружностей всех шести треугольников, образованных медианами, лежат на одной окружности, которая называется окружностью Ламуна. Эта окружность представляет собой ещё один замечательный геометрический объект, связанный с медианами.

Окружность девяти точек

Метрические соотношения

Теорема Аполлония

Длины медиан треугольника связаны с длинами его сторон точными математическими формулами. Для треугольника со сторонами $a,b,c$ соответствующие медианы можно вычислить по формулам:

$m_{a}={\frac {1}{2}}{\sqrt {2b^{2}+2c^{2}-a^{2}}}$

$m_{b}={\frac {1}{2}}{\sqrt {2a^{2}+2c^{2}-b^{2}}}$

$m_{c}={\frac {1}{2}}{\sqrt {2a^{2}+2b^{2}-c^{2}}}$

Эти соотношения, известные как следствия теоремы Аполлония, позволяют вычислить любую медиану, зная длины всех сторон треугольника. Обратная задача также разрешима: по длинам медиан можно восстановить длины сторон исходного треугольника.

Сумма квадратов всех медиан треугольника составляет три четверти от суммы квадратов его сторон. Это соотношение выражается формулой:

$m_{a}^{2}+m_{b}^{2}+m_{c}^{2}={\frac {3}{4}}(a^{2}+b^{2}+c^{2})$

Формула площади треугольника

Площадь треугольника может быть выражена через длины его медиан аналогично формуле Герона. Если $\sigma$ представляет собой полусумму длин медиан ($\sigma =(m_{a}+m_{b}+m_{c})/2$), то площадь $S$ вычисляется по формуле:

$S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}}$

Данная формула особенно полезна в задачах, где длины сторон неизвестны, но заданы медианы треугольника.

Условия ортогональности

Медианы треугольника могут быть взаимно перпендикулярными при выполнении определённых условий. Медианы, проведённые к сторонам длин $a$ и $b$, перпендикулярны тогда и только тогда, когда выполняется соотношение:

$5(a^{2}+b^{2})=c^{2}$

Это условие связывает ортогональность медиан с метрическими характеристиками треугольника и находит применение в задачах на экстремальные свойства геометрических фигур.

Существуют также формулы для вычисления углов между медианой и сторонами треугольника. Если медиана проведена к стороне из вершины, где сходятся стороны длин $p$ и $q$, то углы $\alpha$ и $\beta$ между медианой и этими сторонами определяются через площадь треугольника $S$ и длины сторон:

$\sin \alpha ={\frac {2S}{p\cdot m}},\,\sin \beta ={\frac {2S}{q\cdot m}}$

где $m$ — длина соответствующей медианы. Эти соотношения позволяют полностью определить угловые характеристики медиан относительно сторон треугольника.

Специальные типы треугольников

Равнобедренные треугольники

Равнобедренные треугольники характеризуются особым поведением медиан. Отрезки, идущие от вершин к серединам боковых сторон, всегда равны между собой по длине. При этом медиана, направленная к основанию фигуры, становится многофункциональной линией — она делит угол пополам и перпендикулярна к основанию.

Справедливо и противоположное заключение: равенство двух медиан служит признаком равнобедренности треугольника. Третья медиана при этом приобретает свойства угловой биссектрисы и перпендикуляра к соответствующей стороне. Данная особенность позволяет использовать медианы для идентификации равнобедренных фигур.

Существует специфический случай, при котором медианы к боковым сторонам образуют прямой угол в точке пересечения. Тогда косинусы углов у основания принимают значение 1/4, в то время как косинус противолежащего угла равен —1/2. Подобная геометрическая конфигурация однозначно характеризует определённый тип равнобедренного треугольника.

Медиана, направленная к основанию равнобедренного треугольника, служит линией симметрии всей фигуры. В частном случае равнобедренного прямоугольного треугольника эта медиана разбивает его на пару идентичных прямоугольных треугольников.

Прямоугольные треугольники

Треугольники с прямым углом обнаруживают специфические закономерности в отношении медиан. Отрезок, соединяющий прямоугольную вершину с центром гипотенузы, имеет длину, составляющую ровно половину от длины гипотенузы. Данная особенность превращает медиану в практический инструмент для геометрических построений и расчётов.

Медианы прямоугольного треугольника связаны соотношением:

$m_{a}^{2}+m_{b}^{2}={\frac {5m_{c}^{2}}{4}}$

где $m_{c}$ — медиана к гипотенузе, а $m_{a}$ и $m_{b}$ — медианы к катетам.

Равносторонние треугольники

В равностороннем треугольнике все медианы имеют одинаковую длину и пересекаются под углами 120° друг к другу. Каждая медиана одновременно является высотой, биссектрисой и серединным перпендикуляром соответствующей стороны.

Существует общая закономерность: в любом треугольнике большей стороне соответствует меньшая медиана. Это свойство отражает обратную зависимость между длиной стороны и расстоянием от противоположной вершины до центра этой стороны.

Бесконечно удаленная прямая

Связи с классическими теоремами

Окружность девяти точек

Основания медиан играют важную роль в классической теореме Эйлера об окружности девяти точек. Эта окружность проходит через девять замечательных точек треугольника, включая основания всех трёх медиан, основания высот и середины отрезков от вершин до ортоцентра.

Теорема Теркема устанавливает глубокую связь между медианами и высотами треугольника через окружность девяти точек. Если эта окружность пересекает стороны треугольника в шести точках, то существует взаимосвязь между пересечением медиан и пересечением высот: если медианы пересекаются в одной точке, то и высоты также обязательно пересекаются в одной точке.

Параллельные отрезки

Отрезок, соединяющий основания любых двух медиан, является средней линией треугольника. Это означает, что такой отрезок параллелен третьей стороне треугольника и равен её половине. Данное свойство является следствием теоремы Фалеса и находит широкое применение в решении геометрических задач.

Медианы обладают свойством деления параллельных отрезков: любой отрезок, параллельный стороне треугольника, делится соответствующей медианой пополам.

Расширенные концепции

Сопряжённые линии

В треугольнике существуют линии, сопряжённые с медианами. Симедиана представляет собой отрезок, изогонально сопряжённый с медианой относительно биссектрисы угла. Три симедианы треугольника пересекаются в точке Лемуана, которая обладает собственными замечательными свойствами.

Медиана изотомически сопряжена сама с собой, что означает особую симметрию этой линии в системе изотомических преобразований треугольника. Трилинейная поляра центроида представляет собой бесконечно удалённую прямую, что подчёркивает центральную роль точки пересечения медиан в проективной геометрии.

Обобщения

Медиана является частным случаем более общего понятия чевианы — отрезка, соединяющего вершину треугольника с точкой на противоположной стороне. Когда эта точка совпадает с серединой стороны, чевиана превращается в медиану. Теорема Чевы устанавливает условия, при которых три чевианы пересекаются в одной точке, и медианы представляют собой классический пример выполнения этих условий.

Концепция медианы естественным образом обобщается на многомерные случаи и другие геометрические фигуры, сохраняя при этом основные свойства деления и центрирования. В многоугольниках можно определить аналоги медиан как отрезки, соединяющие вершины с центроидами противоположных сторон или их частей.

В сферической и гиперболической геометриях медианы сохраняют многие из своих свойств, хотя конкретные формулы изменяются в соответствии с метрикой соответствующего пространства. В проективной геометрии медианы связаны с гармоническими отношениями и полярными преобразованиями.

Трёхмерные обобщения

В трёхмерной геометрии аналогом медианы треугольника служит медиана тетраэдра — отрезок, соединяющий вершину тетраэдра с центроидом противоположной треугольной грани. Каждый тетраэдр имеет четыре такие медианы, и все они пересекаются в единственной точке — центроиде тетраэдра.

Центроид тетраэдра делит каждую медиану в отношении 3:1, что отличается от плоского случая и отражает особенности трёхмерной геометрии. Это соотношение известно как теорема Командино и является прямым обобщением свойств медиан треугольника. Медианы тетраэдра играют важную роль в вычислении объёма и центра масс трёхмерных тел, а также в задачах механики и инженерии, связанных с распределением масс в пространстве.

Литература

• Ефремов Д. Новая геометрия треугольника. — Одесса: Типография бланкоиздательства М. Шпенцера, 1902. — 335 с. Архивировано 14 июня 2024 года.
• Стариков В. Н. 10-е исследование по геометрии // Научный рецензируемый электронный журнал МГАУ «Наука и образование». — 2020. — Т. 3, № 1. — С. 7. — ISSN 2658-5642.