Биссектриса

Треугольник ABC с биссектрисой AD

Биссектри́са (от латинского лат. bi- «двойное» и лат. sectio «разрезание») — геометрический луч, исходящий из вершины угла и делящий его на две равные части. Этот фундаментальный элемент геометрии представляет собой множество всех точек, равноудалённых от сторон угла, что делает биссектрису незаменимым инструментом в теоретических исследованиях и практических построениях.

Определение и основные свойства

Согласно академическому определению, представленному в Математической энциклопедии Иваном Борисовичем Ивановым в 1977 году, биссектриса угла представляет внутренний луч, создающий два конгруэнтных угла из исходного. Это определение можно расширить до понимания биссектрисы как геометрического места точек, находящихся на равном расстоянии от сторон угла.

Практическое значение этого свойства становится очевидным при детальном рассмотрении. Если взять любую точку на биссектрисе и провести от неё перпендикуляры к сторонам угла, эти перпендикуляры будут иметь абсолютно одинаковую длину. Например, в угле 80 градусов биссектриса создаст два угла по 40 градусов, а любая точка на этой биссектрисе будет равноудалена от обеих сторон исходного угла.

Математическое обоснование равноудалённости

Доказательство равноудалённости точек биссектрисы от сторон угла основывается на теореме Пифагора и свойствах равнобедренных треугольников. Когда мы берём произвольную точку на биссектрисе и проводим перпендикуляры к сторонам угла, образуются два прямоугольных треугольника.

Эти треугольники имеют общую гипотенузу — отрезок от вершины угла до выбранной точки на биссектрисе. Углы при вершине в обоих треугольниках равны, поскольку биссектриса делит исходный угол пополам. По принципу равенства прямоугольных треугольников по гипотенузе и острому углу, катеты-перпендикуляры оказываются равными.

Типы биссектрис

Внутренние биссектрисы

Внутренние биссектрисы работают с углами, не превышающими 180 градусов. Они располагаются внутри исходного угла и представляют наиболее распространённый тип биссектрис в элементарной геометрии.

Центры трёх вневписанных окружностей (соответственно) образуют — треугольник трёх внешних биссектрис

Особенность внутренних биссектрис заключается в том, что они всегда лежат между сторонами исходного угла. При этом внутренняя биссектриса обладает свойством изогональной сопряжённости сама с собой — если провести отражение биссектрисы относительно любой стороны угла, а затем относительно другой стороны, получится исходная биссектриса.

Внешние биссектрисы

Внешние биссектрисы, детально описанные Эриком Вайсштейном в современных математических ресурсах, работают с дополнительными углами. Они делят пополам угол, образованный одной стороной исходного угла и продолжением другой стороны за вершину.

Принципиальное различие между внутренними и внешними биссектрисами проявляется в их взаимном расположении: они всегда перпендикулярны друг другу. Это означает, что угол между внутренней и внешней биссектрисами любого угла составляет ровно 90 градусов.

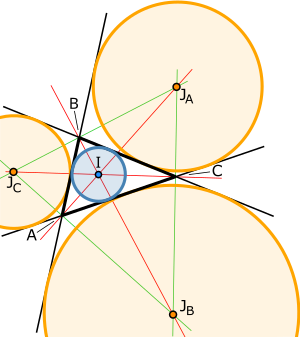
Внешние биссектрисы играют ключевую роль в теории вневписанных окружностей треугольника. Каждая из трёх вневписанных окружностей касается одной стороны треугольника и продолжений двух других сторон. Центры этих окружностей лежат на пересечении одной внутренней и двух внешних биссектрис.

Свойство перпендикулярности

Перпендикулярность внутренней и внешней биссектрис не случайна — она следует из того факта, что сумма смежных углов составляет 180 градусов. Если исходный угол равен $\alpha$, то смежный с ним угол равен $180{\text{°}}-\alpha$. Внутренняя биссектриса делит угол $\alpha$ на две части по $\alpha /2$ каждая. Внешняя биссектриса делит смежный угол на две части по $(180{\text{°}}-\alpha )/2=90{\text{°}}-\alpha /2$.

Угол между биссектрисами составляет: $\alpha /2+(90{\text{°}}-\alpha /2)=90{\text{°}}$. Это свойство остается неизменным для любого угла и создаёт основу для многих геометрических построений и доказательств.

Построение биссектрис

Классический метод

Традиционное построение биссектрисы циркулем и линейкой, известное со времён Евклида, основано на принципе создания равнобедренного треугольника. Метод требует использования циркуля с радиусом, строго превышающим половину расстояния между точками пересечения дуги со сторонами угла.

Алгоритм включает несколько этапов:

1. из вершины угла проводится дуга произвольного радиуса, пересекающая обе стороны угла;
2. из полученных точек пересечения проводятся две дуги одинакового радиуса (больше половины расстояния между точками);
3. прямая, соединяющая вершину угла с точкой пересечения дуг, является искомой биссектрисой.

Геометрическая основа этого построения заключается в том, что получается равнобедренный треугольник, в котором биссектриса основания совпадает с медианой и высотой. Это свойство равнобедренного треугольника гарантирует точное деление исходного угла пополам.

Координатный метод

Алгебраический подход к построению биссектрис, систематизированный Барри Спейном в работе «Аналитические конические сечения» 2007 года, предлагает точные формулы для различных координатных систем. Этот метод особенно важен в компьютерной графике и автоматизированном проектировании.

Внутренняя и внешняя биссектрисы угла, образованного двумя прямыми, перпендикулярны друг другу. Прямые заданы уравнениями:

$l_{1}x+m_{1}y+n_{1}=0$,

$l_{2}x+m_{2}y+n_{2}=0$.

Уравнения внутренней и внешней биссектрис этого угла имеют вид:

${\frac {l_{1}x+m_{1}y+n_{1}}{\sqrt {l_{1}^{2}+m_{1}^{2}}}}=\pm {\frac {l_{2}x+m_{2}y+n_{2}}{\sqrt {l_{2}^{2}+m_{2}^{2}}}}$

Знак «$+$» соответствует внутренней биссектрисе, а знак «$-$» — внешней.

Векторный подход

Перпендикулярная биссектриса отрезка между точками $A$ и $B$ с векторами положения ${\vec {a}}$, ${\vec {b}}$ определяется следующим образом. Середина отрезка, точка $M$, имеет вектор:

${\vec {m}}={\frac {{\vec {a}}+{\vec {b}}}{2}}$

Вектор ${\vec {a}},{\vec {b}}$ задаёт направление отрезка $AB$, биссектриса перпендикулярна ему, поэтому уравнение прямой:

$({\vec {x}}-{\vec {m}})({\vec {a}}-{\vec {b}})=0$

Подстановка ${\vec {m}}$ даёт векторное уравнение:

${\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\frac {{\vec {a}}^{2}-{\vec {b}}^{2}}{2}}$

Для точек $A=(a_{1},a_{2})$ и $B=(b_{1},b_{2})$ в координатах уравнение:

$(a_{1}-b_{1})x+(a_{2}-b_{2})y={\frac {a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}}{2}}$

В явной форме:

$y=m(x-x_{0})+y_{0}$,

где:

$m=-{\frac {b_{1}-a_{1}}{b_{2}-a_{2}}}$,

$x_{0}={\frac {a_{1}+b_{1}}{2}}$,

$y_{0}={\frac {a_{2}+b_{2}}{2}}$.

Треугольник с биссектрисой AD

Ограничения классических построений

Проблема трёх биссектрис

Московский центр непрерывного математического образования установил фундаментальное ограничение классической геометрии: по трём заданным длинам биссектрис невозможно построить треугольник, используя только циркуль и линейку.

Это ограничение связано с тем, что система уравнений, описывающая треугольник через длины его биссектрис, содержит радикалы степени выше второй. Классические построения позволяют решать только квадратные уравнения, что делает задачу принципиально неразрешимой в рамках евклидовой геометрии.

Более того, даже использование трисектора — инструмента для деления угла на три равные части — не решает эту проблему. Трисектор расширяет возможности построений до кубических уравнений, но система уравнений для биссектрис требует решения уравнений более высоких степеней.

Историческая перспектива

Эта невозможность построения аналогична другим знаменитым задачам древности — трисекции угла, квадратуре круга и удвоению куба. Все эти задачи были окончательно решены в XIX веке с развитием теории Галуа, которая точно определила границы возможностей циркуля и линейки.

Пьер Вантсел в 1837 году доказал невозможность трисекции произвольного угла классическими методами. Аналогичные принципы применяются к задаче построения треугольника по биссектрисам — она требует алгебраических операций, недоступных классическим инструментам.

Биссектрисы треугольников

Инцентр и его свойства

Революционные исследования Кларка Кимберлинга в 1994 году систематизировали понимание центральных точек треугольника. Инцентр — точка пересечения всех трёх внутренних биссектрис — обладает уникальными свойствами, делающими его одним из важнейших центров треугольника.

Инцентр является центром вписанной окружности, которая касается всех трёх сторон треугольника изнутри. Расстояние от инцентра до каждой стороны равно радиусу вписанной окружности. Это свойство используется в многочисленных задачах на оптимизацию — например, при поиске максимального круга, помещающегося внутри треугольной области.

Инцентр обладает замечательным свойством деления биссектрис: он разделяет каждую биссектрису в отношении, равном сумме прилегающих сторон к длине противоположной стороны. Математически это записывается как отношение $(b+c):a$ для биссектрисы, проведённой к стороне длиной $a$ из вершины, где сходятся стороны длиной $b$ и $c$.

Практический пример деления биссектрисы

Рассмотрим треугольник со сторонами 5, 12 и 13 единиц (прямоугольный треугольник). Инцентр разделит биссектрису, проведённую к стороне длиной 13, в отношении (5 + 12) : 13 = 17 : 13. Это означает, что отрезок от вершины до инцентра относится к отрезку от инцентра до основания биссектрисы как 17 к 13.

Такая точность деления позволяет использовать инцентр для решения сложных геометрических задач, включая вычисление площадей частей треугольника и определение оптимальных путей внутри треугольных областей.

Центры вневписанных окружностей

Каждый треугольник имеет три вневписанные окружности, каждая из которых касается одной стороны треугольника изнутри и двух других сторон снаружи. Центры этих окружностей (обозначаемые $JA,JB,JC$) лежат на пересечениях внешних биссектрис углов треугольника.

Центры вневписанных окружностей образуют новый треугольник — треугольник трёх внешних биссектрис. Владимир Николаевич Стариков в 2016 году показал, что исходный треугольник является ортотреугольником для этого нового треугольника, то есть стороны исходного треугольника перпендикулярны соответствующим высотам треугольника внешних биссектрис.

Равнобедренные треугольники

Теорема Штейнера-Лемуса

Одним из самых элегантных результатов в теории биссектрис является Теорема Штейнера — Лемуса: если в треугольнике две биссектрисы равны, то треугольник является равнобедренным. Обратное утверждение также справедливо — в равнобедренном треугольнике биссектрисы, проведённые из равных углов, имеют одинаковую длину.

Эта теорема имеет глубокое теоретическое значение, поскольку устанавливает критерий равнобедренности через элементы, отличные от сторон или углов. В практических применениях она позволяет определять симметрию фигур по измерению длин биссектрис.

Доказательство теоремы основывается на анализе формул для длин биссектрис и приводит к выводу о равенстве двух сторон треугольника. Этот результат подчёркивает внутреннюю гармонию геометрических соотношений в треугольнике.

Особая биссектриса равнобедренного треугольника

Третья биссектриса в равнобедренном треугольнике — проведённая из вершинного угла к основанию — обладает уникальным свойством: она одновременно является медианой и высотой. Это тройное совпадение (биссектриса — медиана — высота) происходит только в равнобедренных треугольниках и отражает их совершенную симметрию.

Практически это означает, что биссектриса вершинного угла в равнобедренном треугольнике:

• делит основание пополам (свойство медианы);
• перпендикулярна основанию (свойство высоты);
• делит вершинный угол пополам (собственное свойство биссектрисы).

Это свойство широко используется в инженерных расчётах и архитектурных построениях, где требуется создание симметричных конструкций.

Теорема о биссектрисе

Формулировка и значение

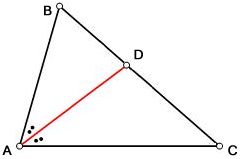
Классическая теорема о биссектрисе, подробно исследованная Роджером Джонсоном в фундаментальной работе «Продвинутая евклидова геометрия» 2007 года, устанавливает точное соотношение между отрезками, на которые биссектриса делит противоположную сторону треугольника.

Теорема утверждает: внутренняя биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам. Математически это записывается как:

$BD:CD=AB:AC$,

где $D$ — точка пересечения биссектрисы угла $A$ с противоположной стороной $BC$.

Доказательство и следствия

Классическое доказательство теоремы основывается на свойствах подобных треугольников или на применении теоремы синусов. Более элегантное доказательство использует равенство площадей треугольников $\triangle ABD$ и $\triangle ACD$, которые имеют одинаковые высоты, проведённые из точки $A$ к основанию $BC$.

Поскольку биссектриса делит угол $A$ пополам, отношение площадей треугольников $\triangle ABD$ и $\triangle ACD$ равно отношению произведений $AB\cdot AD\cdot \sin {\tfrac {\alpha }{2}}$ к $AC\cdot AD\cdot \sin {\tfrac {\alpha }{2}}$, что упрощается до отношения $AB:AC$. С другой стороны, отношение площадей равно отношению оснований $BD:CD$ при одинаковых высотах.

Эта теорема является частным случаем более общей теоремы Штейнера о чевианах — прямых, проходящих через вершины треугольника. Она находит широкое применение в решении задач на нахождение неизвестных элементов треугольника.

Практические применения

Теорема о биссектрисе позволяет решать многочисленные практические задачи. Например, если известны две стороны треугольника и длина отрезка от вершины до точки на третьей стороне, можно определить, является ли этот отрезок биссектрисой, просто проверив пропорциональность.

В инженерии эта теорема используется для определения точек равновесия в конструкциях, где требуется равномерное распределение нагрузок. В компьютерной графике — для алгоритмов интерполяции и создания плавных переходов между различными областями изображения.

Коллинеарность и специальные свойства

Открытие Ефремова

Дмитрий Ефремов в своей работе «Новая геометрия треугольника», опубликованной в Одессе в 1902 году, описал замечательное свойство проекций, связанное с биссектрисами. Если из двух вершин треугольника провести внутренние и внешние биссектрисы, а затем ортогонально спроектировать третью вершину на эти четыре биссектрисы, получившиеся точки проекций будут лежать на одной прямой.

Эта прямая коллинеарности обладает дополнительным свойством: она параллельна стороне треугольника, соединяющей две вершины, из которых были проведены биссектрисы. Данное открытие демонстрирует глубокие скрытые симметрии в геометрии треугольника и показывает, как различные элементы треугольника связаны между собой неочевидными соотношениями.

Геометрический смысл коллинеарности

Коллинеарность проекций отражает фундаментальное свойство треугольника как фигуры, обладающей множественными внутренними симметриями. Каждая проекция вершины на биссектрису создаёт точку, равноудалённую от сторон соответствующего угла.

Тот факт, что четыре такие точки всегда оказываются на одной прямой, указывает на существование скрытых геометрических закономерностей, которые проявляются только при рассмотрении сложных конфигураций элементов треугольника.

Биссектрисы в четырёхугольниках

Циклические и касательные четырёхугольники

Современные исследования Эрика Вайсштейна в математических ресурсах MathWorld показывают, что биссектрисы внутренних углов выпуклого четырёхугольника образуют одну из двух возможных конфигураций. Либо четыре точки пересечения соседних биссектрис лежат на одной окружности (образуют циклический четырёхугольник), либо все биссектрисы пересекаются в одной точке.

Второй случай характеризует касательные четырёхугольники — фигуры, в которые можно вписать окружность, касающуюся всех четырёх сторон. Точка пересечения биссектрис в таком четырёхугольнике является центром вписанной окружности.

Эта дихотомия (либо циклический четырёхугольник из пересечений биссектрис, либо касательный исходный четырёхугольник) отражает глубокие связи между угловыми и метрическими свойствами четырёхугольников.

Мальтитуды и антицентр

Натан Альтшиллер-Корт в работе «Геометрия колледжа» 2007 года описал специальные линии четырёхугольника, называемые мальтитудами. Мальтитуда — это перпендикуляр к стороне четырёхугольника, проведённый через середину противоположной стороны.

В циклических четырёхугольниках (вписанных в окружность) все четыре мальтитуды пересекаются в одной точке, называемой антицентром. Эта точка обладает свойствами, дуальными к свойствам центроида: если центроид связан с медианами и центрами масс, то антицентр связан с перпендикулярными биссектрисами и ортогональными проекциями.

Теорема Брахмагупты

Древнеиндийский математик Брахмагупта (VII век н. э.) установил замечательное свойство ортодиагональных циклических четырёхугольников — четырёхугольников, вписанных в окружность и имеющих перпендикулярные диагонали.

В таком четырёхугольнике перпендикуляр к любой стороне, проведённый из точки пересечения диагоналей, всегда проходит через середину противоположной стороны. Это означает, что точка пересечения диагоналей «видит» все стороны четырёхугольника под прямым углом и делит их пополам своими проекциями.

Ромбы и параллелограммы

Диагонали ромба как биссектрисы

Диагонали ромба обладают уникальным свойством среди всех четырёхугольников: каждая диагональ точно делит пополам пару противоположных углов фигуры. Это делает диагонали ромба одновременно биссектрисами углов, что создаёт внутри ромба четыре равных прямоугольных треугольника.

Данное свойство имеет практическое значение в кристаллографии, где ромбические решётки часто встречаются в структуре минералов. Биссекторные свойства диагоналей ромба используются для вычисления углов между кристаллографическими плоскостями и определения симметрии кристаллов.

Свойства параллелограмма

В параллелограмме любая прямая, проходящая через точку пересечения диагоналей (центр симметрии), обладает замечательным свойством: она делит как площадь, так и периметр фигуры точно пополам.

Это свойство отражает центральную симметрию параллелограмма и используется в различных областях:

• в механике — для нахождения центра масс параллелограммных пластин;
• в оптике — для анализа преломления света в призмах с параллелограммным сечением;
• в архитектуре — для создания симметричных композиций.

Центр параллелограмма является единственной точкой, через которую проходят все прямые, делящие фигуру на две равновеликие части. Это делает его аналогом инцентра для треугольников в контексте деления площади.

Биссектрисы в кривых

Параболы и касательное свойство

В теории конических сечений параболы обладают замечательным свойством, связанным с биссектрисами. Касательная к параболе в любой точке делит пополам угол между прямой, соединяющей эту точку с фокусом параболы, и перпендикуляром к директрисе, проведённым через ту же точку.

Это свойство имеет фундаментальное значение в оптике: параллельные лучи света, падающие на параболическое зеркало, отражаются точно в фокус. Обратно, источник света, помещённый в фокусе параболического рефлектора, создаёт параллельный пучок отражённых лучей.

Окружности и эллипсы

Для окружности и эллипса все линии, делящие площадь и периметр пополам, проходят через центр фигуры. В случае окружности такими биссектрисами являются все диаметры, что отражает совершенную симметрию этой фигуры.

У эллипса биссектрисы площади и периметра также проходят через центр, но только две из них (большая и малая оси) являются осями симметрии. Остальные биссектрисы создают более сложные разбиения эллипса на равновеликие части.

Это свойство используется в астрономии для анализа орбит планет и комет, в инженерии — для расчёта моментов инерции эллиптических деталей, в архитектуре — для создания гармоничных эллиптических пространств.

Точные формулы и вычисления

Длины биссектрис в треугольнике

Виктор Оксман в 2004 году провёл систематическое исследование условий существования треугольников с заданными длинами биссектрис. Его работа установила не только критерии построимости таких треугольников, но и точные формулы для вычисления длин биссектрис через стороны треугольника.

Основная формула для длины биссектрисы, проведённой к стороне c в треугольнике со сторонами $a,b,c$, имеет вид:

$l_{c}={\frac {\sqrt {ab(a+b+c)(a+b-c)}}{a+b}}={\frac {2{\sqrt {abp(p-c)}}}{a+b}}$,

где $p$ — полупериметр треугольника.

Альтернативная тригонометрическая формула выражает длину биссектрисы через стороны и угол:

$l_{c}={\frac {2ab\cos {\tfrac {\gamma }{2}}}{a+b}}$,

где $\gamma$ — угол между сторонами $a$ и $b$.

Формула Лагранжа

Историческая формула Лагранжа предоставляет ещё один способ вычисления длины биссектрисы:

$l_{c}={\sqrt {ab-a_{l}b_{l}}}$,

где $a_{l}$ и $b_{l}$ — длины отрезков, на которые биссектриса $l_{c}$ делит противоположную сторону $c$.

Эта формула особенно полезна в случаях, когда известны не все стороны треугольника, но известны части одной из сторон.

Соотношение Саймонса

Стюарт Саймонс в 2009 году вывел фундаментальное соотношение, связывающее длины всех трёх биссектрис треугольника:

${\frac {(b+c)^{2}}{bc}}l_{a}^{2}+{\frac {(c+a)^{2}}{ca}}l_{b}^{2}+{\frac {(a+b)^{2}}{ab}}l_{c}^{2}=(a+b+c)^{2}$,

$w_{c}^{2}=a_{w}\cdot b_{w}-ab=CE^{2}=BE\cdot AE-ab$.

Это соотношение показывает, что длины биссектрис не независимы — зная любые две из них и стороны треугольника, можно вычислить третью.

Данная формула имеет теоретическое значение для доказательства единственности треугольника с заданными длинами биссектрис и практическое применение в задачах оптимизации формы треугольника.

Расстояния до особых точек

Формулы расстояния до инцентра

Расстояние от любой вершины треугольника до инцентра может быть вычислено несколькими способами. Основная формула связывает это расстояние с радиусом вписанной окружности:

$l_{c0}={\frac {r}{\sin({\frac {\gamma }{2}})}}$,

где $r$ — радиус вписанной окружности, $\gamma$ — угол при вершине, из которой измеряется расстояние.

Альтернативные выражения включают:

$l_{c0}={\frac {r}{\sin({\frac {\gamma }{2}})}}={\sqrt {(p-c)^{2}+r^{2}}}={\sqrt {ab-4Rr}}$,

где $R$ — радиус описанной окружности.

Практическое значение формул

Эти формулы находят применение в различных областях:

• в геодезии — для определения оптимальных точек размещения треугольных опорных пунктов;
• в робототехнике — для планирования движения в треугольных областях;
• в компьютерной графике — для алгоритмов триангуляции и создания сеток.

Точность вычислений особенно важна в инженерных приложениях, где небольшие ошибки в определении положения инцентра могут привести к значительным отклонениям в работе механизмов или конструкций.

Литература

• Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — С. 56.
• Понарин Я. П. Элементарная геометрия. В 2 т.. — М.: МЦНМО, 2004. — С. 30—31.

Ссылки

• Angle Bisector definition. Math Open Reference
• Line Bisector definition. Math Open Reference
• Perpendicular Line Bisector
• Line Bisector