Парабола

Парабола

Пара́бола — одна из классических кривых второго порядка, широко изучаемая в аналитической геометрии и математическом анализе. Это множество точек на плоскости, равноудалённых от заданной точки (фокуса) и заданной прямой (директрисы), не проходящей через фокус.

Геометрические свойства

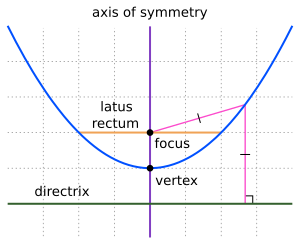
Геометрически парабола представляет собой незамкнутую симметричную кривую с одной осью симметрии, которая проходит через фокус перпендикулярно директрисе. Вершина параболы — точка пересечения кривой с осью симметрии; она расположена ровно посередине между фокусом и директрисой.

Кривая обладает свойством зеркальной симметрии относительно оси и неограниченно простирается в направлении, перпендикулярном директрисе.

Уравнения параболы

В декартовой системе координат простейшее уравнение параболы с вершиной в начале координат и осью симметрии, совпадающей с осью y, имеет вид y = ax², где a ≠ 0 — параметр, определяющий «раскрытие» кривой. При a > 0 ветви параболы направлены вверх, при a < 0 — вниз. Более общий случай описывается квадратичной функцией y = ax² + bx + c, график которой также является параболой, но с вершиной, сдвинутой относительно начала координат.

В полярных координатах (с началом в фокусе и полярной осью вдоль оси симметрии) уравнение принимает вид r = ${\frac {p}{1-\cos \theta }}$, где p — фокальный параметр (расстояние от фокуса до директрисы). В параметрической форме параболу y = ax² описывают уравнения x = t, y = at², где t — </nowiki>параметр.

Оптическое свойство и его применение

Важное свойство параболы — оптическое: лучи, исходящие из фокуса, после отражения от параболической поверхности идут параллельно оси симметрии. И наоборот, параллельный пучок лучей, падающий на параболическое зеркало вдоль оси симметрии, собирается в фокусе.

Это свойство находит широкое применение в технике: параболические антенны, прожекторы, телескопы‑рефлекторы. Используют форму параболы для фокусировки электромагнитных волн или света.

Физические приложения

В физике парабола описывает траекторию тела, брошенного под углом к горизонту в однородном поле тяжести. Данное описание предполагает отсутствие сопротивления воздуха.

В небесной механике параболические орбиты соответствуют граничному случаю между замкнутыми (эллиптическими) и разомкнутыми (гиперболическими) траекториями. Тело, движущееся по параболической орбите, имеет ровно вторую космическую скорость относительно притягивающего центра.

Дополнительные характеристики

Парабола обладает рядом характерных геометрических свойств, вытекающих из её определения как конического сечения. В частности, её эксцентриситет строго равен единице, что служит одним из формальных признаков параболы в классификации кривых второго порядка.

Длина дуги параболической кривой выражается посредством интеграла, который не удаётся свести к комбинации элементарных функций, что придаёт вычислению протяжённости участка кривой определённую сложность. Площадь сегмента, ограниченного параболой и хордой, определяется специальной формулой, учитывающей параметр квадратичной зависимости a и координаты точек пересечения хорды с параболой.

Прикладное значение

Параболические формы широко распространены в самых разных сферах человеческой деятельности. В архитектуре они находят применение при создании арочных конструкций, обеспечивающих прочность и выразительность сооружений.

В инженерной практике параболическая форма естественным образом возникает в подвесных мостах, где цепь под равномерной нагрузкой принимает именно такой изгиб. Экономисты используют параболические кривые при построении графиков квадратичных функций, описывающих полезность или издержки, а специалисты по компьютерной графике — для моделирования гладких кривых и поверхностей, в том числе с применением сплайновых методов.