Эллиптическая кривая

Наука
Математика
Тема	эллиптическая кривая
Предмет изучения	действия с точками на кривой
Период зарождения	XVII век
Основные направления	математика, аналитическая геометрия
Вспомогат. дисциплины	алгебра, математический анализ, криптография
Значительные учёные	Ньютон, Вейерштрасс, Даниэл Бернштайн, Таня Ланге

Эллипти́ческая крива́я над полем $K$ — это геометрическое множество точек на плоскости, удовлетворяющее уравнению 3-й степени с коэффициентами из поля $K$ и «точкой на бесконечности» (бесконечно удалённая точка):

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

Дополнительные определения:

• поле в общей алгебре — множество, для элементов которого определены операции сложения, взятия противоположного значения, умножения и деления (кроме деления на ноль), причём свойства этих операций близки к свойствам обычных числовых операций. Наиболее известными полями являются поле рациональных чисел, поле действительных чисел и поле комплексных чисел;
• группа — множество, на котором определена ассоциативная бинарная операция, причём для этой операции имеется нейтральный элемент (аналог единицы для умножения) и каждый элемент множества имеет обратный (зеркальный) элемент.

Эллиптические кривые являются одним из основных направлений в современной теории чисел. Например, они были использованы Эндрю Уайлсом (совместно с Ричардом Тейлором) в доказательстве Великой теоремы Ферма. Они примененяются в криптографии, в частности, на эллиптических кривых основан российский стандат цифровой подписи ‎ГОСТ Р 34.10-2001. Большинство криптографических протоколов полагаются на конечные поля, то есть поля с конечным числом элементов.

История

Древнейшим дошедшим до нашего времени источником, в котором рассматриваются кубические кривые, является «Арифметика» древнегреческого математика Диофанта. В этой работе ставится задача найти рациональные и нетривиальные решения уравнения $y(6-y)=x^{3}-x$. Диофант решает эту задачу при помощи подстановки $x=3y-1$.

В 1670-х годах Ньютон, используя приёмы аналитической геометрии, делает попытку классифицировать кубические кривые. В ходе исследований Ньютон заметил, что решение Диофанта состоит, по существу, в пересечении кривой, заданной уравнением $y(6-y)=x^{3}-x$, с касательной $x=3y-1$.

Открытие Ньютона в конечном итоге привело к формулам сложения точек на эллиптической кривой. В XIX веке эллиптические кривые находят применение в теории эллиптических функций, тесно связанных с эллиптическими интегралами, которые называются так потому, что они используются, в частности, для вычисления длины дуг эллипсов. Таким образом, исторически термин «эллиптическая кривая» происходит от термина «эллиптический интеграл».

Эллиптические кривые над полем действительных чисел

Если характеристика поля (Char K, от англ.character), над которым рассматривается данное уравнение, не равна 2 или 3,  то уравнение с помощью замены координат (преобразование координат производится для перехода к более простой или более удобной для анализа математической модели) приводится к одной канонической форме — форме Вейерштрасса:

$y^{2}=x^{3}+ax+b$

Как видно из формулы, если точка с координатами ($x,y$) удовлетворяет приведённому уравнению, то этому уравнению удовлетворяет также и точка с координатами ($x,-y$).

В случае если характеристика поля $K$ равна 3, общее уравнение кривой можно привести к следующей форме:

$y^{2}=x^{3}+ax^{2}+b\quad$

Наконец, если характеристика поля $K$ равна 2, общее уравнение кривой можно привести к одной из следующих форм:

$y^{2}+xy=x^{3}+ax^{2}+b\quad$

$y^{2}+cy=x^{3}+ax+b\quad$

Во всех указанных случаях коэффициенты $a$ и $b$ (либо $a$, $b$ и $c$) являются элементами поля $K$ и являются вещественными числами.

Определение эллиптической кривой также требует, чтобы кривая не имела особых точек. Геометрически это значит, что график не должен иметь самопересечений. Алгебраически достаточно проверить, что дискриминант $\Delta =-16(4a^{3}+27b^{2})$ не равен нулю.

Графики эллиптических кривых

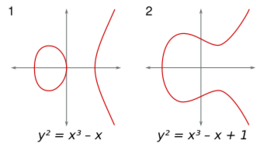
График эллиптической кривой может иметь две формы:

• Если дискриминант положительный, он состоит из двух компонентов (как на изображении слева, где кривая имеет дискриминант 64). Этот случай соответствует тому факту, что кубический многочлен $x^{3}+ax+b$ имеет ровно три различных действительных корня; эти корни являются абсциссами трех точек эллиптической кривой на оси $x$ .
• Если дискриминант отрицательный, он имеет только один компонент (как на изображении справа, где кривая имеет дискриминант -368). Этот случай соответствует тому факту, что кубический многочлен $x^{3}+ax+b$ имеет ровно один действительный корень. Этот корень — абсцисса точки эллиптической кривой на оси $x$ .

Примеры арифметических операций над точками на эллиптической кривой

Геометрическое сложение точек на эллиптической кривой

Сложение двух точек на эллиптической кривой стало возможным благодаря следующему свойству: секущая прямая, проходящая через две точки кривой, пересекает кривую в третьей точке.

На множестве точек эллиптической кривой определяют группу по сложению точек эллиптической кривой. Операцией группового сложения называют три точки эллиптической кривой, удовлетворяющих уравнению:

$R+P+Q=0$.

Поскольку точке с координатами ($x,y$) с точки зрения алгебры удовлетворяет также и точка с зеркальными координатами ($x,-y$), имеем так же и зеркальное отображение $R^{'}=-R$, то есть элементы $R^{'}$, $R$ являются взаимно обратными по групповой операции.

В этом случае суммой двух точек $P$ и $Q$, принадлежащих эллиптической кривой, называется третья точка, которая лежит на секущей прямой $PQ$ и эллиптической кривой одновременно и обозначается как:

$P+Q=R^{'}$

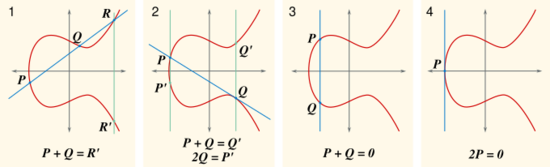
Итак, в общем случае для групповой операции по сложению необходимо провести секущую через точки $P,Q$ и зеркально отобразить точку $R$ как $R^{'}=-R$

Существуют следующие частные случаи:

• Если прямая $PQ$ является касательной к кривой в одной из двух точек, мы считаем, что третья точка пересечения $R$ одновременно является точкой касания $Q$. Это говорит о том, что касательная имеет двойной контакт с кривой: $P+Q=Q^{'}$

• Если прямая $PQ$ вертикальна, мы считаем, что третья точка пересечения $R$ является точкой на бесконечности и что она сама по себе симметрична относительно оси $x$. Таким образом, сумма двух точек — это бесконечно удаленная точка: $P+Q=0$
• Наконец, чтобы определить сумму точки к себе ($P+P$, или $2P$ ), используем касательную в точке $P=Q$. Она пересекает кривую в третьей точке, сумма точек равна $2P=0$.

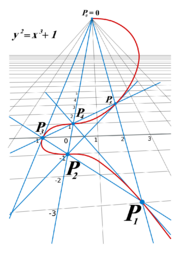
Умножение точек на эллиптической кривой

Сложение естественным образом позволяет определить умножение точки на кривой на целое число. Например,$-3*P$ по определению равно $-(P+P+P)$. Но может случиться так, что возникнет необходимость в других видах умножения.

Например, в случае кривой, определённой уравнением $y^{2}=x^{3}-x$, можно применить процедуру умножения на комплексное число $i$ (его ещё называют «мнимая единица»), равное ${\sqrt {-1}}$, задав точку с координатами $P(-x,iy)$, и в более общем плане мы можем получить умножение точек кривой на любое целое число Гаусса.

Для эллиптических кривых, определенных на полях характеристики «ноль» (например, поле рациональных чисел), это, по сути, единственные два возможных случая: либо есть только умножение на относительные целые числа, либо есть комплексное умножение на порядок в мнимом квадратичном поле.

Эллиптические кривые в криптографии

Создание криптографии с открытым ключом Диффри и Хеллманом в 1976 году и последующее изобретение криптосистемы с открытым ключом RSA Ривестом, Шамиром и Адлеманом в 1978 году являются переломными событиями в долгой истории секретных коммуникаций. Трудно переоценить важность электронных систем с открытым ключом и связанных с ними схем цифровой подписи в современном мире компьютеров и интернета.

Криптография – это метод защиты информации путём использования специальных алгоритмов кодирования. Информация может находиться на этапе хранения (например, файл на жестком диске), передачи (например, электронная связь между двумя или несколькими сторонами) или использования для вычислений.

Поскольку практически вся информация, используемая в настоящее время, существует в цифровом виде, любое сообщение $M$можно представить в виде какого-то целого числа. Мы можем зашифровать его, используя выражение $C=M*G$, где $C$ — это зашифрованная посылка, а $G$ — это какой-то множитель, изменяющий (шифрующий) исходный код посылки.

Вопрос в том, насколько сложно, имея зашифрованный текст $C$ и не зная множитель, восстановить исходное сообщение $M$, если в процедуре шифрования были использованы операции сложения и умножения над точками эллиптической кривой. При этом нужно учитывать, что арифметические операции с точками на эллиптической кривой не эквивалентны арифметическим операциям с их координатами.

Данная задача называется дискретным логарифмированием на эллиптической кривой и не имеет быстрого решения, поскольку методы решения дискретного логарифма на эллиптической кривой имеют сложность порядка:

$O({\sqrt {n}})$

где $n$ — количество точек эллиптической кривой.

Таким образом, даже при использовании самого быстрого алгоритма для решения задачи дискретного логарифмирования на эллиптических кривых, необходимо $O({\sqrt {n}})$ операций. При этом размер поля должен как минимум в два раза превосходить размер ключа, для 128-битового ключа рекомендуется использовать эллиптическую кривую над полем $\mathbb {F} _{p}$, где p имеет длину 256 бит.

Для примера: ключ над полем характеристики 2 был найден с использованием 2600 компьютеров в течение 17-ти месяцев .

Электронная цифровая подпись с использованием эллиптических кривых

Электронная подпись предназначена для защиты электронного документа, передаваемого посредством различных сред или хранящегося в цифровом виде, от подделки и является атрибутом электронного документа. Она получается в результате криптографического преобразования информации с использованием закрытого ключа электронной цифровой подписи и позволяет идентифицировать владельца сертификата ключа подписи, установить отсутствие искажения информации в электронном документе.

Федеральным законом от 06 апреля 2011 года № 63-ФЗ «Об электронной подписи» определены три вида электронной подписи:

• простая электронная подпись
• неквалифицированная электронная подпись
• квалифицированная электронная подпись

Электронная подпись работает по асимметричному принципу шифрования. То есть документ зашифровывается с помощью закрытого ключа, а расшифровывается с помощью открытого.

Основной алгоритм ECDSA (англ.Elliptic Curve Digital Signature Algorithm — алгоритм цифровой подписи эллиптической кривой) принят в качестве стандартов ANSI X9F1 и IEEE P1363.

Создание ключей

1. Выбирается эллиптическая кривая $E_{p}(a,b)$. Число точек на ней должно делиться на большое простое число $n$.
2. Выбирается базовая точка $G\in E_{p}(a,b)$ порядка $n$, $n\cdot G=\infty$.
3. Выбирается случайное число $d\in (1,n)$.
4. Вычисляется $Q=d\cdot G$.

Создание подписи

1. Выбирается случайное число $k\in (1,n)$.
2. Вычисляется $k\cdot G=(x_{1},y_{1})$ и $r=x_{1}(\operatorname {mod} n)$.
3. Проверяется условие $r\neq 0$, так как иначе подпись не будет зависеть от закрытого ключа. Если $r=0$, то выбирается другое случайное число $k$.
4. Вычисляется $k^{-1}(\operatorname {mod} n)$.
5. Вычисляется $s=k^{-1}\cdot (H(M)+dr)(\operatorname {mod} n)$.
6. Проверяется условие $s\neq 0$, так как в этом случае необходимого для проверки подписи числа $s^{-1}(\operatorname {mod} n)$ не существует. Если $s=0$, то выбирается другое случайное число $k$ .

Подписью для сообщения $M$ является пара чисел ($r$, $s$).

Проверка подписи

1. Проверим, что числа $r$ и $s$ принадлежат диапазону чисел ($1$, $n$). В противном случае результат проверки отрицательный и подпись отвергается.
2. Вычислить $w=s^{-1}(\operatorname {mod} n)$ и $H$($M$).
3. Вычислить $u_{1}=H(M)w(\operatorname {mod} n)$ и $u_{2}=rw(\operatorname {mod} n)$.
4. Вычислить $u_{1}G+u_{2}Q=(x_{0},y_{0}),v=x_{0}(\operatorname {mod} n)$.
5. Подпись верна в том и только том случае, когда $v$ = $r$.

Литература

• Клеменс, Г. Мозаика теории комплексных кривых. — М.: Мир, 1984.
• Лебедев П.А., Нестеренко А.Ю.Арифметика на эллиптических кривых с использованием графических вычислителей.— М.: Чебышевский сборник, том 13, выпуск 2, 2012.

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!