Комплексное число

Наука
Математика
Тема	Комплексное число
Предмет изучения	понятия и представления комплексных чисел
Период зарождения	XVI век
Основные направления	Высшая математика теория функций комплексного переменного
Вспомогат. дисциплины	алгебра, геометрия, математический анализ, высшая алгебра

Комплексное число (от лат. complexus — связь, сочетание) выражение вида${\begin{alignedat}{2}x+iy\end{alignedat}}$,где ${\begin{alignedat}{2}x\end{alignedat}}$ и ${\begin{alignedat}{2}y\end{alignedat}}$- действительная числа, а второе ${\begin{alignedat}{2}i\end{alignedat}}$ — мнимая единица $i^{2}=-1$.

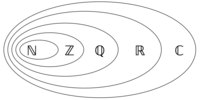
Комплексные числа вида Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ z=x+0i=x} являются действительными числами. Комплексные числа вида $\ z=0+yi=yi$ называются чисто мнимыми числами. Это означает, что множество R всех действительных чисел является подмножеством всех комплексных чисел C. Число ${\begin{alignedat}{2}x\end{alignedat}}$ называется действительной частью комплексного числа и обозначается ${\begin{alignedat}{2}x=Rez\end{alignedat}}$ , а ${\begin{alignedat}{2}y\end{alignedat}}$ мнимой частью ${\begin{alignedat}{2}z\end{alignedat}}$, ${\begin{alignedat}{2}y=Imz\end{alignedat}}$.

Два комплексных числа $\ z_{1}=x_{1}+iy_{1}$ и $\ z_{2}=x_{2}+iy_{2}$ называются равными Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ z_{1}=z_{2}} тогда и только тогда, когда равны их действительные части и равны их мнимые части: $\ x_{1}=x_{2}$, $\ y_{1}=y_{2}$. В частности, комплексное число равно нулю тогда и только тогда, когда $\ x=y=0$. Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Определение. Два комплексных числа $\ x+iy$ и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ x-iy} , действительные части которых равны, а мнимые различаются только знаками, называются сопряженными. Число сопряженное к$\ z=x+iy$ обозначается чертой, поставленной над ним: $\ {\bar {z}}=x-iy$.

Геометрическое изображение комплексных чисел

Изображение комплексного числа на плоскости

Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу $\ z=x+yi$ ставится в соответствие точка $\ (x,y)$ координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части-ординату точки. Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой. Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам $\ x+0i$ соответствуют точки оси абсцисс, а чисто мнимым числам Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ 0+yi} , точки оси ординат. Поэтому ось $\ Oy$ называют мнимой, а ось $\ Ox$ действительной. Сопряженным комплексным числам $\ z=x+yi$ и $\ z=x-yi$ соответствуют точки, симметричные относительно оси абсцисс.

Точка координатной плоскости. соответствующая комплексному числу $\ z=x+yi$, может быть указана по-другому: её координатами могут быть расстояние $\ r$ от начала координат и величина угла $\ \varphi$ между положительной полуосью $\ Ox$ и лучом $\ Oz$ . Расстояние $\ r$ от начала системы координат до точки, соответствующей комплексному числу $\ z$, называют модулем этого числа. Тогда по теореме Пифагора имеем: $\ r^{2}=x^{2}+y^{2}=(x+yi)(x-yi)=z\cdot z$. Отсюда найдем модуль комплексного числа как арифметическое (неотрицательное) значение корня: $\ |z|=|{\bar {z}}|={\sqrt {x^{2}+y^{2}}}$ . Если комплексное число $\ z$ изображается точкой оси абсцисс (то есть является действительным числом), то его модуль совпадает с абсолютным значением. все комплексные числа, имеющие модуль 1, изображаются точками единичной окружности- окружности с центром вначале системы координат, радиуса 1. Угол $\ \varphi$ между положительной полуосью $\ Ox$ и лучом $\ Oz$ называют аргументом комплексного числа $\ z=x+yi$. Сопряженные комплексные числа $\ z=x+yi$ и $\ {\bar {z}}=x-yi$ имеют один и тот же модуль $\ |z|=|{\bar {z}}|={\sqrt {x^{2}+y^{2}}}$ и аргументы отличаются знаком: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ \varphi =-\varphi } .

В отличие от модуля аргумент комплексного числа определяется неоднозначно. Аргумент одного и того же комплексного числа может иметь бесконечно много значений и определяется с точностью до слагаемого $\ 2\pi k(k=0,-1,1,-2,2...):$$\ \operatorname {Arg} z=\operatorname {arg} z+2\pi k$, где $\ \operatorname {arg} z=\varphi$ — главное значение аргумента, заключенное в промежутке Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ (-\pi ;\pi ]} , то есть $\ -\pi <\operatorname {arg} z\leq \pi$.

Формы записи комплексных чисел

Запись числа ${\begin{alignedat}{2}z\end{alignedat}}$ в виде ${\begin{alignedat}{2}x+iy\end{alignedat}}$ называют алгебраической формой комплексного числа.

Комплексное число в виде ${\begin{alignedat}{2}x+iy\end{alignedat}}$ использует декартовы координаты точки, соответствующей этому числу. Положение точки на плоскости вполне определяется, однако, также заданием её полярных координат: расстояния $\ r$ от начала координат до точки и угла $\ \varphi$ между положительным направлением оси абсцисс и направлением из начала координат на эту точку. Между декартовыми и полярными координатами точки существует следующая связь, справедливая при любом расположении точек на плоскости:Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ x=r\cos \varphi } , $\ x=r\sin \varphi$. Следовательно комплексное число $\ z=x+iy$ можно записать в виде

$\ z=r(\cos \varphi +i\sin \varphi )$. Такая запись комплексного числа называется называется тригонометрической формой.

Модуль $\ r=|z|$ однозначно определяется по формуле $\ r=|z|={\sqrt {x^{2}+y^{2}}}$

Аргумент $\ \varphi$ определяется из формул $\ \cos \varphi ={\frac {x}{r}}$, $\ \sin \varphi ={\frac {y}{r}}$, $\ \operatorname {tg} \varphi ={\frac {y}{x}}$.

Так как $\ \varphi =\operatorname {Arg} z=\operatorname {arg} z+2k\pi =$, то Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ \cos \varphi =\cos(\operatorname {arg} z+2k\pi )=\cos(\operatorname {arg} z)} $\ \sin \varphi =\sin(\operatorname {arg} z)$.

Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа $\ z$, то есть считать Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ \varphi =\operatorname {arg} z} .

Так как $\ -\pi <\operatorname {arg} z\leq \pi$, то из формулы $\ \operatorname {tg} \varphi ={\frac {y}{x}}$ находим $\ \varphi =\operatorname {arg} z={\begin{cases}\operatorname {arctg} {\frac {y}{x}},x<0;\\\operatorname {arctg} {\frac {y}{x}}+\pi ,x<0,y>0;\\\operatorname {arctg} {\frac {y}{x}}-\pi ,x<0,y<0.\end{cases}}$

Во многих случаях использования комплексных чисел применяется показательная форма их записи. Для получения этой формы используется формула Эйлера: $\ e^{i\varphi }=\cos \varphi +i\sin \varphi$ вывод которой основывается на знании степенных рядов. Представим комплексное число в тригонометрической форме: $\ z=r(\cos \varphi +i\sin \varphi )$. На основании формулы Эйлера получим показательную форму комплексного числа Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\begin{alignedat}{2}z=re^{i\varphi }\end{alignedat}}} .

Действия над комплексными числами в алгебраической форме

• Сложение (аналитическая формула)

Суммой двух комплексных чисел $\ z_{1}=x_{1}+iy_{1}$ и $\ z_{2}=x_{2}+iy_{2}$ называется комплексное число, определяемое равенством:

$\ z_{1}+z_{2}=(x_{1}+iy_{1})+(x_{2}+iy_{2})=(x_{1}+x_{2})+i(y_{1}+y_{2})$

Правило сложения комплексных чисел можно сформулировать следующим образом: при сложении комплексных чисел складываются отдельно их действительные части и отдельно их мнимые части.

Полученный результат легко обобщается на случай любого числа слагаемых:

$\ z_{1}+z_{2}+\ldots +z_{n}=(x_{1}+x_{2}+\ldots +x_{n})+i(y_{1}+y_{2}\ldots +y_{n})$ , где $\ z_{1}=x_{1}+iy_{1}$; $\ z_{2}=x_{2}+iy_{2}$;…;$\ z_{n}=x_{n}+iy_{n}$.

Операция сложения комплексные чисел обладает следующими свойствами:

Коммутативность (сумма комплексных чисел не зависит от порядка слагаемых (переместительный закон))

$\ z_{1}+z_{2}=z_{2}+z_{1}$

Ассоциативность (слагаемые можно объединять в группы (сочетательный закон)

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://wikimedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \ (z_{1}+z_{2})+z_{3}=z_{1}+(z_{2}+z_{3})}

Дистрибутивность

$\ z_{1}(z_{2}+z_{3})=z_{1}z_{2}+z_{1}z_{3}$

Сложение комплексных чисел геометрически выполняется по правилу параллелограмма, то есть по правилу сложения векторов, выходящих из начала координат.

• Вычитание

Вычитание определяется как действие, обратное сложению . Разностью двух комплексных чисел $\ z_{1}$ и $\ z_{2}$ называется такое комплексное число $\ z$, которое, будучи сложенным с $\ z_{2}$, дает число Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1 } , то есть Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z=z_1- z_2 } , если Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z+z_2=z_1 } . Если Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1= x_1+iy_1} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_2= x_2+iy_2} , то из этого определения легко получить Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z } :

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1-z_2=(x_1+iy_1)-(x_2+iy_2)=(x_1+x_2)-i(y_1+y_2)} :

Геометрически вычитание векторов сводится к сложению вектора уменьшаемого с вектором, по величите равным вычитаемому, по направлению ему противоположным.

• Умножение

Произведением комплексных чисел Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1= x_1+iy_1} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_2= x_2+iy_2} , называется комплексное число, определяемой равенством

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1 \cdot z_2=(x_1+iy_1)\cdot (x_2+iy_2)=x_1x_2+ix_1y_2+ix_2y_1+i^2y_1y_2} (как произведение буквенных многочленов).

Приняв во внимание, что Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ i^2=-1} , и группируя действительные и мнимые части, находим

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ (x_1+iy_1)\cdot (x_2+iy_2)=(x_1x_2-y_1y_2)+i(x_1y_2+y_1x_2)} .

Операция умножения комплексные чисел обладает следующими свойствами:

Коммутативность (сумма комплексных чисел не зависит от порядка слагаемых (переместительный закон))

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1 z_2=z_2 z_1}

Ассоциативность (слагаемые можно объединять в группы (сочетательный закон)

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ (z_1 z_2) z_3=z_1 ( z_2 z_3)}

Дистрибутивность

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1(z_2+z_3)=z_1 z_2+z_1z_3}

• Деление

Деление комплексных чисел определяется как действие, обратное умножению: если Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z= z_1 : z_2} , то частное Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z} есть число, удовлетворяющее равенству Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ zz_2= z_1 } .

Частное двух комплексных чисел находят путем умножения и числителя и знаменателя на числа, сопряженное знаменателю, в результате чего получим

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{z_1}{z_2}=\frac{z_1 \bar{z_2}}{z_2 \bar{z_2}}= \frac{(x_1+iy_1)(x_2-iy_2)}{x_2^2+y_2^2} }

и окончательно

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ \frac{z_1 }{z_2} =\frac{(x_1+iy_1)}{(x_2+iy_2)}=\frac{(x_1x_2+y_1y_2)}{(x_2^2+y_2^2)}+i\frac{(y_1x_2-x_1y_2)}{(x_2^2+y_2^2)}} .

Действия над комплексными числами в тригонометрической форме

Умножение

Правило умножения комплексных чисел Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1=r_1(\cos\varphi_1+i\sin\varphi_2)} и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_2=r_2(\cos\varphi_1+i\sin\varphi_2)} , заданных в тригонометрической форме:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1\cdot z_2=r_1\cdot r_2(\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2))} .

В результате приходим к следующей формулировке: произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей и аргумент- сумме аргументов сомножителей.

Рассматривая Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1\cdot z_2} как одно комплексное число, формулу легко распространить на случай трех сомножителей, а затем и на случай любого числа сомножителей, то есть

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z_1\cdot z_2 \cdot \cdot \cdot z_n =r_1\cdot r_2 \cdot \cdot \cdot r_n (\cos(\varphi_1+\varphi_2+\cdot \cdot \cdot+\varphi_n)+i\sin(\varphi_1+\varphi_2+\cdot \cdot \cdot+\varphi_n))} .

Деление

Деление комплексных чисел определяется как действие обратное умножению и осуществляется по формуле

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ \frac{z_1}{z_2}= \frac{r_1(\cos\varphi_1+i\sin\varphi_2)}{r_2(\cos\varphi_1+i\sin\varphi_2)} =\frac{r_1}{r_2}(\cos(\varphi_1-\varphi_)+i\sin(\varphi_1-\varphi_2))} .

Отсюда вытекает также, что модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.

Из этих правил выводятся законы, позволяющие возводить комплексное число Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z } в любую степень и извлекать из него корень.

Возведение в степень и извлечение корня из комплексных чисел

Применяя формулу произведения комплексных чисел в тригонометрической форме в случае Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } равных сомножителей, получим правило возведения в степень комплексных чисел: Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ z^n=r((\cos\varphi+i\sin\varphi))^n=r^n(\cos n \varphi+i\sin n \varphi)} ,

то есть для возведения комплексного числа в целую положительную степень нужно его модуль возвести в эту степень, а аргумент умножить на показатель степени.

Полагая в формуле Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r=1 } , получаем формулу Муавра названную по имени английского математика Абрахама де Муавра (Abraham де Moivre, 1667—1754), нашедшего её в 1707 г .

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ (\cos\varphi+i\sin\varphi)^n=\cos n \varphi+i\sin n \varphi} .

Формула Муавра позволяет наиболее просто выводить тригонометрические формулы для синусов и косинусов кратных углов. Разлагая левую часть данного равенства по формуле бинома Ньютона и приравнивая отдельно вещественные и мнимые части, получим выражения для Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \cos n \varphi } и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sin n \varphi } через степени Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \cos \varphi } и Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \sin \varphi } .

Извлечение корня Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } степени определяется как действие, обратное возведению в натуральную степень. Корнем Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } степени из комплексного числа Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle z=r(\cos\varphi+i\sin\varphi) } называется такое комплексное число Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle a=\rho (\cos\alpha+i\sin\alpha) } , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } -я степень которого равна подкоренному числу: Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle a^n=z } . Таким образом, получаем:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ \sqrt[n]{r(\cos\varphi+i\sin\varphi)}=\sqrt[n]{r}(\cos\frac{\varphi+2\pi k}{n}+i\sin\frac{\varphi+2\pi k}{n})} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ k=0,1,...,n-1} ,

то есть для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня.

Таким образом, извлечение корня Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } -й степени из комплексного числа Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle z } всегда возможно и дает Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } различных значений. При других значениях Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle k } , в силу периодичности косинуса и синуса, получатся значения корня, совпадающие с уже найденными. Геометрически эти Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } значений изобразятся вершинами некоторого правильного Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } угольника, вписанного в окружность, с центром в начале координат, радиуса Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ \sqrt[n]{r}} . В частности, корень Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } -й степени из единицы имеет Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } различных значений, которые являются вершинами правильного Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle n } -угольника, вписанного в единичный круг, причем одна из его вершин есть единица. В виде формулы эти корни записываются следующим образом:

Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ \sqrt[n]{1}=\cos\frac{2 k\pi}{n}+i\sin\frac{2 k \pi}{n}} , Невозможно разобрать выражение (SVG с запасным PNG (MathML можно включить с помощью плагина для браузера): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ (k=0,1,...,n-1)} .

Историческая справка

Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы иероглифы нелепых количеств.Л. Карно

Если рассматривать только действительные числа, то операция извлечения квадратного корня, обратная к операции возведения в квадрат, не всегда возможна, так как нельзя извлечь квадратный корень из отрицательного числа. Этого, однако, недостаточно, чтобы заводить в математике новые числа. Оказалось, чо если производить вычисления по обычным правилам над выражениями, в которых встречается корень квадратный из отрицательного числа, то можно прийти к результату, уже не содержащему корень квадратный из отрицательного числа. В XVI веке Кардано нашел формулу для решения кубического уравнения. Оказалось, что именно в том случае, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается корень квадратный из отрицательного числа. Обнаружилось таким образом, что, производя вычисления с выражениями, содержащими корень квадратный из отрицательного числа можно получить вполне понятные результаты. Поэтому эти корни стали употреблять в математике. Назвали их мнимыми числами- тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам на грани XVIII—XIX столетий дал Гаусс, который назвал их комплексными числами, дал им геометрическую интерпретацию и, что самое главное, доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный или комплексный корень.

Ссылки

• Понтрягин Л. Комплексные числа