Великая (последняя) теорема Ферма

Великая теорема Ферма́ (или последняя теорема Ферма́) — одна из самых популярных теорем математики. Сформулирована французским математиком Пьером Ферма в 1637 году. Название «Последняя теорема Ферма» обязано своим происхождением тому обстоятельству, что среди многих теорем, которые Ферма сформулировал без доказательства, эта теорема оставалась последней не доказанной.

Несмотря на простоту формулировки, доказательство теоремы искали многие математики на протяжении более трёхсот лет. И только в 1994 году теорема была доказана английским математиком, профессором Принстонского университета, Эндрю Уайлсом с коллегами. Публикация доказательства состоялась в 1995 году.

Формулировка

«Арифметика» Диофанта Александрийского с записью Ферма

Пьер Ферма, читая «Арифметику» Диофанта Александрийского и размышляя над её задачами, имел привычку записывать на полях книги результаты своих размышлений в виде кратких замечаний. Против восьмой задачи Диофанта на полях книги, Ферма записал:

«Кубу невозможно быть суммой двух кубов, четвёртой степени невозможно быть суммой двух четвёртых степеней, или, в общем, любому числу, представляющему собою степень, большую второй, невозможно быть суммой двух таких же степеней. Я открыл воистину чудесное доказательство этого предположения, для размещения которого здесь эти поля слишком узки»

Если перевести эту цитату в алгебраическую форму записи, то теорема Ферма утверждает, что для любого целого положительного числа $n>2$ уравнение:

$a^{n}+b^{n}=c^{n}$

не имеет решений в целых положительных числах $a,b,c$, отличных от нуля.

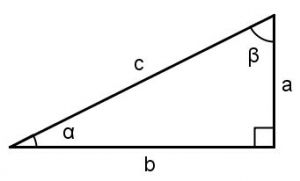
Ферма записал это уравнение в той части книги «Арифметика» Диофанта, где речь шла об известной теореме Пифагора, которая утверждает, что в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Если $a$ и $b$ являются катетами прямоугольного треугольника, а $c$ - гипотенузой, то в алгебраической форме записи уравнение примет вид:

$a^{2}+b^{2}=c^{2}$

что является частным случаем от общего уравнения при показателе степени $n=2$ (пифагорейское уравнение).

Приведём пример поиска численного значения гипотенузы по известным значениям катетов в области целых положительных чисел:

допустим, $a=3$, $b=4$, тогда сумма их квадратов составит число $9+16=25$, а число $c={\sqrt[{2}]{25}}=5$.

Мы получили тройку чисел, $3,4,5$, которые удовлетворяют уравнению при показателе степени $n=2$.

Стороны треугольника можно измерять в любых одинаковых единицах, поэтому теорема Пифагора справедлива для любых чисел, однако в их множестве существует бесконечное количество таких троек целых положительных чисел $a,b,c$, из которых можно построить прямоугольные треугольники, длины сторон которых выражены целыми числами. Эти числа называют пифагоровыми тройками.

Доказательств теоремы Пифагора более или менее строгих, более или менее наглядных – известно несколько сотен, начиная от древнеиндийского математика Басхары до векторного доказательства.

Вернёмся к теореме Ферма и приведём пример поиска значения числа $c$, если показатель степени $n>2$, например $n=3$. В этом случае при тех же значениях $a=3$, $b=4$, сумма кубов этих чисел составит число $27+64=91$. Тогда искомое значение числа $c={\sqrt[{3}]{91}}=4.4979414452754$, то есть целым числом не является.

Ферма утверждал, что при целом положительном показателе степени $n>2$ решение для $a,b,c$ в области целых положительных чисел не существует в принципе и это утверждение потребовало для своего доказательства сотни лет поисков самых известных математиков. Немалую лепту в этот процесс внесла именно простота написания. Нет другого математического утверждения, обладающего такой простотой формулировки, из которой логически ожидаемо должно вытекать столь же несложное доказательство.

Кроме того, сам Ферма написал на полях книги Диофанта: «Я открыл воистину чудесное доказательство этого предположения, для размещения которого здесь эти поля слишком узки». Эта фраза стала основным стимулом к поискам доказательства, так как Ферма утверждал непреложный факт его существования, а поскольку Ферма располагал теми же знаниями, что и его современники, к тому же он был юристом, а не профессиональным математиком, значит для доказательства теоремы требовалось лишь сделать какой-то необычный ход.

Всё оказалось гораздо сложнее.

История доказательства

Поскольку сам Ферма нашел доказательство этой теоремы лишь для $n=4$, а его доказательство для произвольного $n$ не было найдено исследователями, математики решили доказать (или опровергнуть) высказанное им утверждение. Ведь до тех пор, пока математическое сообщество в целом не восстановит доказательство, все утверждения рассматриваются лишь как гипотезы. На протяжении последних 350 лет Великую теорему Ферма правильнее было бы называть Великой гипотезой Ферма.

В основном удавались попытки найти доказательство для некоторых конкретных значений числа $n$ .

Для $n=3$ великую теорему Ферма доказал Леонард Эйлер, для $n=4$ доказательство привели П. Дирихле и А. Лежандр (1825 год), для $n=7$ – французский математик, механик, физик и инженер Г. Ламе (1839 год). Появление компьютеров значительно расширило возможности для доказательства. После Второй мировой войны группы программистов и математиков доказали Великую теорему Ферма при всех значениях $n$ до $500$, затем до $1000$, а позже до $10000$. В 80-е годы Сэмюэль Вагстафф поднял предел до $25000$, а в 90-х математики заявили, что Великая теорема Ферма верна при всех значениях $n$ до $4$ миллионов. Но все это были частные случаи, строгого доказательства теоремы Ферма представлено не было.

В результате математическое сообщество пришло к выводу, что нужно искать другие пути, существующими в математике типовыми методами проблему доказательства в общем виде не решить.

Английский математик Г. Г. Харди кратко выразил дух доказательства от противного в своей книге «Апология математика»:

«Reductio ad absurdum, столь любимое Евклидом, — одно из самых прекрасных орудий математика. Это гораздо более тонкий гамбит, чем любая шахматная партия: шахматист может пожертвовать пешкой или даже какой-нибудь фигурой, но математик жертвует партией».Г. Г. Харди

Оказалось, что теорема Ферма не укладывается в прокрустово ложе линейной действительной оси, когда существует однозначное соответствие между множеством действительных чисел и множеством точек, равномерно расположенных на прямой. Другими словами, существуют такие действительные числа, для операций с которыми нужны другие формы представления.

Усилия математиков привели к получению многих важных результатов современной теории чисел. Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (8 августа 1900 года) отметил, что поиск доказательства для этой, казалось бы, малозначимой теоремы привёл к глубоким результатам в теории чисел:

«Известно утверждение Ферма о том, что диофантово уравнение

$a^{n}+b^{n}=c^{n}$

неразрешимо в целых числах, если не считать известных очевидных исключений. Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побужденный задачей Ферма, Куммер пришел к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители - теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций»

Разновидность эллиптической кривой

В 1984 году немецкий математик Герхард Фрай доказал, что решение теоремы Ферма можно включить в некоторое эллиптическое уравнение и предположил, что Великая теорема Ферма является следствием теоремы Таниямы — Симуры, которая гласит:

«каждой эллиптической кривой соответствует определенная модулярная форма (функция, определённая на верхней комплексной полуплоскости, то есть на множестве {$G={x+iy}$}, где $i={\sqrt {-1}}$ )».

Предположение было доказано Кеном Рибетом.

Эндрю Уайлс рядом со статуей Пьера де Ферма в Бомонте-де-Ломань.

Тем самым Фрай сделал сенсационный вывод о том, что если бы математикам удалось доказать теорему Таниямы — Симуры, то они автоматически доказали бы последнюю теорему Ферма. Но в течение последующих тридцати лет после появления в 1955 году теоремы Таниямы — Симуры доказать её не удавалось. Надежд на успех не прибавлялось до тех пор, пока доказательство в сентябре 1994 года не представил американский математик, профессор Принстонского университета, Эндрю Уайлс.

Оно заняло 130 страниц машинописного текста, математик работал над ним в течение семи лет. Небольшой пробел в доказательстве удалось устранить с помощью соавтора и ученика Уайлса — Ричарда Тейлора, и в мае 1995 года был представлен окончательный вариант доказательства.

В марте 2016 года Президент Норвежской Академии наук и литературы (норв. Det Norske Videnskaps-Akademi, DNVA) Оле Сейерстед заявил, что «в этом году Абелевской премии — одной из крупнейших премий по математике (её называют «Нобелевской премией по математике») — удостоился математик Эндрю Уайлс, доказавший Великую теорему Ферма.» Как говорилось в сообщении, опубликованном на сайте премии, своим доказательством профессор Принстонского университета Эндрю Уайлс «открыл новую эру в теории чисел». Награду математик получил 24 марта из рук кронпринца Норвегии Хокона в рамках торжественной церемонии в Осло.

«Ферматисты»

Простота формулировки теоремы Ферма, а также сложность единственного известного доказательства (или незнание о его существовании), вдохновляют многих на попытки найти другое, более простое, доказательство. Людей, пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками». Ферматисты зачастую не являются профессионалами и допускают ошибки в арифметических действиях или логических выводах, хотя некоторые представляют весьма изощрённые «доказательства», в которых трудно найти ошибку.

Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил её следующей припиской:

«Редакция „Кванта“ со своей стороны считает необходимым известить читателей, что письма с проектами доказательств теоремы Ферма рассматриваться (и возвращаться) не будут».

Немецкому математику Эдмунду Ландау очень докучали «ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сотен бланков с шаблонным текстом, сообщающим, что на определённой строке на некоторой странице находится ошибка, при этом находить ошибку и заполнять пробелы в бланке он поручал своим аспирантам:

Уважаемый …! Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на стр. … в строке …

Теорема Ферма в науке и искусстве

Само по себе доказательство теоремы Ферма представляет интерес только для специалистов в области математической теории. Важным является тот факт, что в процессе доказательства были разработаны или дополнены разделы математики, которые активно используются. Это такие направления, как алгебраическая геометрия, аналитическая теория чисел. В физике было создано направление нелинейной квантовой механики. Наука о шифровании (криптография), основанная на свойствах эллиптических кривых, тоже получила своё развитие. Это защита электронных документов, цифровые подписи. Поскольку свойства эллиптических кривых очень тесно связаны с уравнением Ферма, то вклад в это направление неоспорим.

В 2008 году был издан научно-фантастический роман Артура Кларка и Фредерика Пола «Последняя теорема». По одной из сюжетных линий студент Раджит стремится найти альтернативное доказательство Великой теоремы Ферма, что в конечном итоге приводит его к пониманию закулисы мировой политики.

Почтовая марка, посвящённая Великой теореме Ферма

В 2000 году по инициативе ЮНЕСКО (англ. UNESCO; United Nations Educational, Scientific and Cultural Organization) отмечался Всемирный год математики. В честь этого события в Чехии была выпущена почтовая марка, посвящённая Великой теореме Ферма.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!