Симметрия
Симме́трия (лат. symmetria, греч. συμμετρία — соразмерность) — особое свойство объектов или явлений, которое характеризуется тем, что они могут быть разделены на части, симметричные относительно некоторой оси, плоскости или центра[1]. В природе существует несколько видов симметрии, каждый из которых имеет свои особенности. В всех её формах она выражает гармонию и равновесие. В природе сочетание симметрии и асимметрии образует неповторимое и разнообразное множество форм и узоров[2].
Искусство и архитектура также нередко играют с симметрией, используя её для создания эстетического впечатления[3]. Симметрия сердца и души может быть идеальной, так и незначительно нарушенной, что придаёт неповторимость каждому человеку.
Всего лишь одинаковость форм и фигур не в силах создать такую эмоциональную привязанность, как гармоничное сочетание симметрии и именно того, что делает нас уникальными. Симметрия имеет не только эстетическую ценность, но и практическое применение. Она играет важную роль в дизайне и создании симметричных и гармоничных композиций. Кроме того, симметричные формы и структуры могут быть более устойчивыми и функциональными. Исследование симметрии также позволяет углубить понимание форм и их взаимодействия, что имеет фундаментальное значение в математике и физике[4].
Симметрия в геометрии
Симметрия является одним из основных понятий геометрии, которое имеет широкое применение в различных областях. Она определена как свойство фигур, при котором части объекта или сам объект отражаются относительно определённой оси, плоскости или центра. Это свойство исследуется и применяется в геометрии, искусстве, архитектуре, физике и многих других областях.
Осевая симметрия
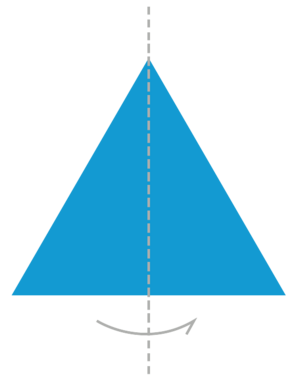
Осевая симметрия возникает, когда фигура разделяется на две равные и зеркально отражающиеся части относительно оси. Это обычный вид симметрии, который можно часто наблюдать в природе. Такие объекты, как лица людей, обладают осевой симметрией[2].
Зеркальная симметрия
Зеркальная симметрия или отражение (симметрия относительно плоскости) — это движение в евклидовом пространстве, при котором множество точек, оставшихся неподвижными, образует гиперплоскость (в трёхмерном пространстве просто плоскость). Термин «зеркальная симметрия» также используется для описания типа симметрии объекта, когда объект при отражении отображается в самого себя[5]. Зеркальная симметрия проявляется во многих законах природы, включая кристаллографию, химию, физику, биологию и другие науки, а также в искусстве и искусствоведении.
Центральная симметрия
Центральная симметрия (симметрия относительно точки) происходит, когда фигура отражается относительно центральной точки. Этот вид симметрии часто встречается в геометрии, особенно в круговых и сферических фигурах. При центральной симметрии относительно точки О, фигура Ф совпадает с самой собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей. Другими словами, точка О является серединой отрезка, соединяющего симметричные точки Ф[5].
Симметрия в других науках
Алгебра
Изучением симметрии в алгебре занимались советские математики Н. Я. Виленкин (1920—1991), В. Г. Болтянский (1925—2019) и другие. В алгебре симметрия означает, что выражение или объект остаётся неизменным при некотором преобразовании. Это может быть симметрия относительно оси или плоскости, симметрия относительно поворота или перестановки элементов. Симметрия в алгебре позволяет упростить вычисления и анализировать свойства алгебраических выражений. Одним их примеров симметрии в алгебре являются симметрические многочлены. Симметрическими многочленами называются многочлены, которые не меняются при перестановке переменных. Например, многочлены x² + y² и xy + yx являются симметрическими, так как они равны и не изменяются при замене x на y, y на x[6]. Симметрические многочлены важны в теории алгебраических уравнений. Корни симметрического многочлена сохраняются при рациональных преобразованиях, что позволяет находить новые корни, основываясь на известных.
Биология
Билатеральная симметрия является одной из основных форм симметрии у живых организмов. Она характеризуется разделением организма на две симметричные половины, которые являются, по сути, зеркальным отражением друг друга. У двусторонне симметричных организмов можно выделить верхнюю (спинную), нижнюю (брюшную) и боковые стороны тела. Это особенно характерно для различных групп животных, таких как черви, членистоногие, хордовые.
У растений билатеральная симметрия прослеживается в строении некоторых органов, например листьев. Однако, в большинстве случаев организмы имеют некоторые отклонения от идеальной билатеральной симметрии. Примером такого отклонения является у человека смещение сердца в левую сторону тела. Билатеральная симметрия имеет важное значение для организмов, так как позволяет более эффективно использовать ресурсы окружающей среды и выполнять различные функции[7].
Физика
Симметрия в физике означает, что физическая система остается неизменной после определённых преобразований или операций. Это свойство подчеркивает инвариантность системы, то есть её неизменность при сохранении определённых условий[8].
- Непрерывные пространственно-временные симметрии (перенос, поворот, изменение начало отсчёта времени).
- Дискретная симметрия (для описания некоторых симметрий элементарных частиц или кристаллических структур).
- Зарядовая симметрия (определяются множество свойств элементарных частиц).
- СР-симметрия, или комбинированная инверсия, является процессом, при котором одновременно осуществляется инверсия пространственных координат и зарядового состояния[9].
Искусство
Симметрия в искусстве является важным и часто используемым принципом композиции. Она подразумевает равенство и соразмерность частей соответствующих друг другу элементов произведения искусства. Симметричная композиция обладает структурной упорядоченностью и гармонией, создавая впечатление баланса и совершенства[10].
Примеры симметрии можно найти во многих областях искусства. В живописи, например, симметричные композиции могут быть достигнуты путём размещения симметричных объектов или форм на полотне, как, например, в симметрично расположенных фигурах людей или симметричных элементах пейзажа. В архитектуре симметрия может быть воплощена в виде симметричного размещения и повторения элементов здания, таких как окона, двери или колонны. Симметрия также часто используется в дизайне и разработке логотипов, где она может быть использована для создания эстетического и легко запоминающегося образа.
Асимметрия
Асимметрия (др.-греч. ασυμμετρία, букв. «несоразмерность» от μετρέω «измеряю») — отсутствие симметричности или равномерности в определённом объекте, явлении или процессе. Асимметрия проявляется в том, что соответствующие структуры или элементы обладают различными формами, размерами или расположением. Это свойство не только придаёт предметам или явлениям уникальность, но и играет важную роль в множестве научных исследований и приложений. Понятие асимметрии тесно связано с ощущением гармонии и баланса. Ведь именно в неравномерности находится привлекательность и эстетическое воздействие, которое оказывает на нас объект или композиция. Благодаря асимметрии возникает возможность раскрыть новые перспективы и видеть мир с необычной стороны[11].
Асимметрия широко распространена в природе, будь то анатомические особенности животных, геометрия кристаллов, или даже взаимодействие элементарных частиц[11].
В мире искусства и дизайна, асимметрия также является ключевым элементом, позволяющим создавать великолепные и запоминающиеся произведения. Асимметрия — это не только отличительная черта объектов и явлений, но и ключевой элемент творчества и познания. В ней заключены неожиданные формы и уникальные сочетания, которые позволяют нам восхищаться, размышлять и расширять свой взгляд на окружающий мир[3].
Примечания
- ↑ Симметрия. Большая российская энциклопедия (22 сентября 2023). Дата обращения: 19 марта 2024.
- ↑ 2,0 2,1 Шафранский И. И. Симметрия в природе. — Л.: Недра, 1985. — С. 17—35. — 168 с.
- ↑ 3,0 3,1 Березин Д. В. Симметрия и асимметрия // Наука, образование и культура : Журнал. — 2018. — № 4 (28). — ISSN 2413-7111.
- ↑ Асламазова З.С. Симметрия — основополагающий принцип устройства мира. КиберЛенинка — научная электронная библиотека. Дата обращения: 25 марта 2024.
- ↑ 5,0 5,1 Выгодский М. Я. Справочник по элементарной математике. — М.: Государственное издательство технико-теоретической литературы, 1954. — С. 319—320. — 412 с.
- ↑ Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М.: МЦНМО, 2002. — С. 8—9. — 240 с. — ISBN 5-94057-041-0.
- ↑ Иорданский Н. Н. Билатеральная симметрия (в биологии). БРЭ. Большая российская энциклопедия (14 сентября 2022). Дата обращения: 20 марта 2024.
- ↑ Тищенко, И. Ю. Роль симметрии в теоретической физике // Молодой ученый : Журнал. — 2022. — № 1(396). — С. 3—6.
- ↑ Герштейн С. С. Симметрия. Большая российская энциклопедия - электронная версия. Дата обращения: 23 марта 2024.
- ↑ Симметрия. Краткий словарь по эстетике. Дата обращения: 23 марта 2024.
- ↑ 11,0 11,1 Морфогенез в индивидуальном и историческом развитии: симметрия и асимметрия (Серия «Гео-биологические процессы в прошлом») / Отв. ред. С.В. Рожнов.. — М.: ПИН РАН, 2013. — 330 с. — ISBN 978-5-903825-37-0.
Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело! |