Паттерн
Па́ттерн (англ. pattern — «шаблон, образец») — это повторяющаяся структурная модель, которая служит посредником между восприятием и мышлением для выявления закономерностей в окружающем мире. Данная концепция представляет воспроизводимую схему, а её элементы демонстрируют систематическое повторение. Из визуальных паттернов формируются декоративные узоры[1].
Чувственные органы воспринимают паттерны согласно собственным характеристикам.
В научных дисциплинах, включая математику и языкознание, они обнаруживаются через исследовательскую деятельность.
Прямое наблюдение обеспечивает выявление визуальных моделей в их естественном формировании и художественных произведениях. Природные визуальные паттерны характеризуются хаотичностью. Они не дублируют друг друга и зачастую обладают фрактальными свойствами.
Естественные паттерны включают спиральные структуры, извилистые линии, волновые образования, пенные формации, трещинообразные структуры, а также модели, образованные вращательной и отражательной симметрией. Они обладают математически формализуемой структурой, выражаемой через формулы, при этом математика сама по себе представляет поиск закономерностей, поэтому любой финальный результат функционального применения составляет математический паттерн.
Исследование и предсказывание научными концепциями синхронных закономерностей в природе и социуме, это и является выявлением паттернов.
В живописи и архитектуре орнаментальные элементы и разнообразные визуальные компоненты сочетаются и воспроизводятся, создавая образцы для достижения конкретного устойчивого эффекта.
В информационных науках проектировочные шаблоны являются широко используемым подходом к решению обширного спектра программных задач.
В медицинской сфере термин обозначает устойчивое сочетание исследовательских данных или иных признаков при аналогичных жалобах у пациентов или больных одной нозологической категории. Понятие «паттерн» охватывает множественные признаки. Синдром включает один или несколько паттернов. Патология охватывает один или несколько синдромов.
Естественные паттерны
Древнегреческие философы, включая Платона, Пифагора, Эмпедокла, изучали паттерны, пытаясь раскрыть природную упорядоченность. Современное понимание визуальных паттернов развивалось поэтапно с прогрессом наук.
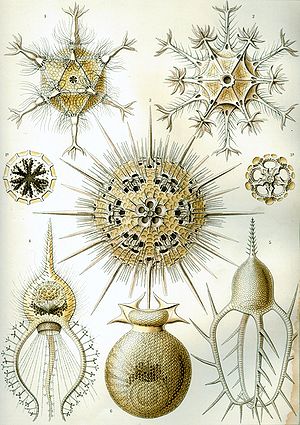
В XIX веке бельгийский физик Ж. Плато при исследовании мыльных пузырей разработал концепцию минимальной поверхности. Немецкий биолог и художник Э. Геккель изобразил сотни морских существ, подчёркивая их симметричность. Шотландский биолог Д. Томпсон впервые приступил к изучению паттернов роста растительных и животных организмов, показав, что спиральный рост можно описать элементарными уравнениями. В XX веке английский математик А. Тьюринг спрогнозировал морфогенетические процессы, отвечающие за образование пятен, спиралей и полос. Венгерский биолог А. Линденмайер и французский математик Б. Мандельброт продемонстрировали, как фрактальная математика раскрывает паттерны растительного развития.
Математические, физические и химические науки объясняют естественные паттерны на разных уровнях. Паттерны живых существ объясняются биологическими механизмами естественного и полового отбора[2]. Исследование паттернообразования применяет компьютерное моделирование для имитации широкого диапазона паттернов.
Симметрия
Симметричность для биологических организмов составляет практически универсальное явление. Большинство представителей животного мира обладает зеркальной или билатеральной симметричностью, которая также присутствует в листовых пластинах и отдельных цветках, таких как орхидеи[2].
Растения зачастую имеют радиальную или ротационную симметрию, что характерно для множества цветковых форм и отдельных представителей животного мира, например кишечнополостных. Пятилучевая симметричность характерна для иглокожих организмов, включая морских звёзд, морские ежей и морских лилий.
В неживой природе снежинка демонстрирует изящную шестилучевую симметричность. Несмотря на то, что каждая снежинка индивидуальна, единообразный паттерн встречается на всех шести лучах. Кристаллические образования обычно обладают различными формами симметрии и габитусами, такими как кубические, шестигранные, восьмигранные, но никогда не демонстрируют пятилучевую симметрию.
Ротационная симметрия встречается в различных неорганических процессах, например при капельном всплеске в водоёме, а также в планетарных сферических конфигурациях и кольцевых системах планет наподобие Сатурна.
Древовидные структуры, фракталы
Фракталы характеризуются самоподобием[3]. Бесконечные повторения в природных условиях невозможны, поэтому такие паттерны фрактальны лишь приблизительно. К примеру, листва папоротников и зонтичных (Apiaceae) самоподобна на 2-4 уровне. Аналогичные папоротнику паттерны самоподобия обнаруживаются и у животных, включая мшанок, кораллы, гидроидных, а также в неорганической природе, главным образом в электрических разрядах.
Фракталоподобные паттерны широко представлены в таких обычных феноменах, как облачные образования, речные системы, разломы земной коры, горные массивы, береговые контуры, окраска животных, снежинки, кристаллы, сосудистые разветвления и морские волны.
Спиральные формы
Спирали часто наблюдаются у растений и некоторых животных, главным образом моллюсков. У наутилусов каждая камера раковины представляет примерную копию предшествующей, увеличенную на конкретный коэффициент и представленную как логарифмическая спираль[4]. Основываясь на современном понимании фракталов, развивающаяся спираль составляет частный случай самоподобия.
Среди растительности спирали формируют некоторые виды алоэ. Также спирально размещены листья на стебле и других частях растений: соцветиях астровых, семенных головка подсолнечника, плодах ананаса и салака, на шишках, где множественные спирали размещаются как по часовой, так и против часовой стрелки.
Такой рост листьев может выводиться из последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13…, где каждое последующее число составляет сумму двух предшествующих. К примеру, при листовом росте из ствола, один спиральный поворот соответствует двум листьям, поэтому паттерн или пропорция составляет 1/2. У орешника пропорция 1/3; у абрикоса 2/5; у груши 3/8; у миндаля она составляет 5/13.
Хаотичность, потоки, меандры
В математических науках динамическая система считается хаотической, если она излишне чувствительна к начальным условиям. Это называется «эффект бабочки»[5].
Теория хаоса рассматривается как один из ключевых факторов, воздействующих на формирование паттернов в природе. Существует взаимосвязь между хаосом и фракталами — странные аттракторы в хаотических системах обладают фрактальной размерностью.
Турбулентность в газообразных и жидких средах при преодолении твёрдого препятствия формирует характерные паттерны вращения.
Меандры представляют синусоидальные изгибы в речных руслах и других каналах, создаваемые жидкостью, обычно водой, протекающей по изгибам. Если русло не является равномерным, размеры и неровность изгибов возрастает из-за перемещения течением твёрдого материала, обычно песка и гальки к внутренней части изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая скорость меандрирования.
Волновые структуры, дюны
Под воздействием ветровых потоков на водной и песчаной поверхности в природе формируются аналогичные по структуре хаотические паттерны. Они оставляют рябь, которая называется волнами на воде и дюнами на песке. Из-за воздействия ветра происходит неравномерное распределение, в результате возвышенные участки сменяются понижениями уровня. Особым случаем дюн выступают барханы[6].
Волновые паттерны на водной поверхности проявляют ритмичные структуры, изменяющиеся в зависимости от ветровой силы, глубины водоёма и подводного рельефа. Песчаные дюны создают сложные модели в зависимости от направления доминирующих ветров. В пустынях образуются поперечные, продольные и звёздчатые дюны, каждая из которых демонстрирует уникальную адаптацию к местным ветровым условиям.
Пузырчатые образования, пена
Мыльные пузыри создают пену при накоплении. В XIX веке бельгийский физик Жозеф Плато, исследуя мыльные пузыри, разработал концепцию минимальной поверхности. Пенные структуры демонстрируют математические закономерности минимизации поверхностного натяжения.
Естественная пена возникает на морском побережье в результате взаимодействия волн с органическими компонентами в воде. Эти пенные паттерны демонстрируют временную структуру, постоянно трансформирующуюся под влиянием приливов и волнения. Пенообразование в естественных условиях зависит от концентрации органических веществ, солёности воды и интенсивности волнового воздействия[7].
Замощающие структуры
Замощение составляет разделение без наложений и пустот. Наиболее известным примером замощения в природе служат пчелиные соты, где шестигранная структура многократно воспроизводится, заполняя всё пространство улья. Она оптимальна для сот с позиции материального использования и максимизации объёма при минимальных восковых затратах[8].
Кристаллические структуры минералов также проявляют замощающие паттерны. Базальтовые столбы формируются при лавовом остывании, создавая естественные геометрические паттерны шестигранного сечения. Базальтовые лавовые потоки часто образуют столбчатые срастания, которые при остывании создают трещины, из которых формируется замощение.
Явление наблюдается в высохших илистых отложениях, где возникают полигональные сети трещин. Их размер зависит от толщины высыхающего слоя, скорости влагоиспарения и минерального состава грунта.
Трещинные образования
Трещины образуются в материалах вследствие температурного воздействия: 120-градусного в эластичных материалах, и 90-градусного в неэластичных материалах. Подобные явления широко распространены в природе, например в горных породах, высохшей грязи, древесной коре и глазурях старинных картин и керамики[9].
Трещинообразование в засушливых почвах формирует полигональные модели, размер которых определяется толщиной высыхающего слоя и скоростью влагоиспарения. В арктических областях морозное растрескивание грунта создаёт подобные регулярные сети, видимые с воздуха.
Термические трещины в горных породах образуют характерные паттерны, зависящие от минералогического состава, структуры породы и температурных колебаний. Базальтовые плато демонстрируют столбчатую форму — регулярные шестигранные призмы, формирующиеся при медленном остывании лавы.
Пятнистость и полосатость
В 1952 году, ещё до биологического открытия двойной спирали ДНК, Алан Тьюринг, математик, создатель современных вычислительных машин, выдвинул смелую теорию происхождения животных узоров. Согласно его предположению, ткани в процессе развития производят химические агенты, которые смешиваются, а точнее диффундируют через ткани.
Американские исследователи разгадали механизм появления необычной животной окраски: полос, линий и пятен. Узоры появляются благодаря диффузиофорезу. Когда химические агенты диффундируют через ткани, как описал Тьюринг, они также увлекают пигментные клетки посредством диффузиофореза, подобно тому, как мыло извлекает загрязнения из белья[10].
Архитектурные паттерны
В архитектурной сфере паттерн представляет повторяющуюся структуру, проявляющуюся в фасадах зданий, интерьерах или планировке. Она используется для создания гармонии и функциональности. К примеру колоннады, повторяющиеся арки или фасадные орнаменты служат важным дизайнерским элементом[11].
Архитектурный орнамент с древнейших времён является выразительным средством, в котором сочетаются цветовые решения, фактура, ритмичность, симметрия, повторяемость рисунка, рельефная глубина. Архитектурный орнамент берёт своё начало из культуры глубокой древности, примерно 15-10 тыс. лет до н. э. Ранние декоративные элементы, украшающие строения, несли сакральный смысл, либо применялись для подчёркивания фасадной симметричности сооружений.
Древний архитектурный узор основывался преимущественно на элементарных геометрических фигурах: окружности, квадрате, зигзаге, треугольнике. Однако уже тогда встречались спиралевидные рисунки, полоски, верёвочный и ёлочный узоры. Треугольники символизировали горы, окружности — солнце, спираль — движение и жизнь. В некоторых этносах архитектурный орнамент в виде знаков-пиктограмм был начальной стадией возникновения письменности.
В архитектурном узоре Египта нередко фигурирует лотос — цветок или лепестки — это символ богини Исиды, означающий природную силу, чистоту, здоровье, магию. Лотос также олицетворял солнце. Также применялись папирусы, тростники, лилии цветы, пальмовые листья, акации, терновника и тутового дерева листья, которые означали Жизненное Древо.
Современная архитектура применяет паттерны для создания визуальной динамики и пространственного структурирования. Модульные строительные системы основаны на повторяющихся элементах, обеспечивающих экономичность и эстетическую целостность зданий. Фасадные паттерны могут включать геометрические композиции из стекла, металла и бетона, создающие световую и теневую игру.
Дизайнерские паттерны
Повторяющиеся декоративные элементы используются для оформления повседневных объектов — от архитектурной лепнины, мощения дорожек, настенных покрытий, напольных материалов и плитки до текстильных орнаментов, декорирования тканей и узорного оформления полиграфической продукции. Среди наиболее востребованных паттернов выделяются шахматная клетка, «гусиная лапка», огурцы, пейсли, греческий ключ, меандр. Орнаменты активно применяются в исламской живописи. Специалисты по искусствоведению классифицируют мусульманские узоры на растительные стилизации, именуемые арабеской, и геометрические композиции, называемые мореской[11].
Декоративные паттерны строятся на классических орнаментах, вдохновлённых историческими или этническими мотивами. Внедрение подобных паттернов в дизайн-проекты способно обеспечить бренду узнаваемый и глубокий культурный имидж.
Известные паттерны включают:
- Пейсли — восточный орнамент каплевидной формы.
- Шеврон — зигзагообразный узор из угловых элементов.
- Nova Check — фирменная клетка Burberry.
Детские паттерны
Элементарным инструментом для создания паттернов служит спирограф. Наблюдать причудливые узоры возможно с помощью калейдоскопа[12].
Образовательное значение паттернов в детском развитии трудно переоценить. Работа с ними развивает логическое мышление, аналитические способности и пространственное восприятие. Принципы, заложенные в основу конструкторов, мозаики и пазлов, способствуют развитию математического мышления.
Простейшие паттерны в детских играх включают чередование цветов, форм и размеров. Нанизывание бусин позволяют создавать цветовые и размерные последовательности. Танграм и другие геометрические головоломки развивают понимание пространственных паттернов.
Игровые модели в раннем детстве начинаются с простых повторений: хлопки в ладоши, топанье ножками, звуковые повторы. Эти действия формируют чувство ритма. Музыкальные игрушки с цикличными мелодиями помогают детям понять принципы музыкальных паттернов.
Медицинские паттерны
В клинической практике понятие используют при интерпретации диагностических данных, таких как электрокардиограммы, электроэнцефалограммы и результатов прочих исследований. Под этим подразумевается устойчивая последовательность биоэлектрических сигналов, воспроизводящихся в одном или нескольких отведениях при аналогичных условиях и состояниях[13].
Данный термин обозначает определённую последовательность нейронных сигналов, несущую конкретное содержание, к примеру «болевые паттерны при биомеханических дисфункциях суставов краниовертебрального сочленения и цервикального отдела позвоночника» или «паттерны моторных и сенсорных нарушений при поражении нервных структур в дистальных сегментах верхней конечности».
Паттерн широко используется и в терминологии мануальных терапевтов, рефлексотерапевтов и специалистов по прикладной кинезиологии. Локомоторный паттерн исследуется для выявления патологии опорно-двигательной системы, респираторный — для оценки функционального состояния органов дыхания.
Вязальные паттерны
Орнаментальные схемы, воспроизводящиеся через заданное число петельных рядов и столбиков, применяются в рукоделии. Они созданы для систематического воспроизведения в трикотажном изделии и именуются паттерном. Схемы могут формироваться из разнообразных типов петель, создавая рельефный узор, либо образовываться через повторение орнамента из нитей различной окраски, например стилизованные растительные мотивы или анималистические изображения на пуловерах[14].
Классические рукодельные паттерны транслировались из поколения в поколение и обладали характерными региональными чертами. Скандинавские, кельтские, альпийские орнаменты отражали культурные традиции и природную среду регионов.
Музыкальные паттерны
Вся современная музыка зачастую основана на паттернах. К ним относится повторяющаяся мелодия (мотив, или как его ещё называют «хук»), ритмический рисунок, басовая партия, пэды, синтезаторные или гитарные риффы[15].
Ритмические паттерны создают основу музыкальных жанров. Различные музыкальные стили характеризуются специфическими ритмическими структурами — от классического вальса с его трёхдольным размером до сложных мотивов африканской музыки.
Современная электронная музыка активно применяет зацикленные паттерны — лупы, создающие основу для дополнительных элементов наслоения. Программные секвенсоры позволяют создавать и модифицировать модели в реальном времени, что открывает новые возможности для творчества.
Примечания
- ↑ Цахаева А. А., Сиражудинова Р. Р., Аминова Д. К. Паттерны реального и виртуального мира в сознании личности // Успехи современной науки и образования. — 2016. — Т. 3, №. 4. — С. 32—35.
- ↑ 2,0 2,1 Болл Ф. Закономерности в природе: самотканый ковёр. Формы / Ф. Болл. — М.: Издательство студии Артемия Лебедева, 2025. — С. 11.
- ↑ Mandelbrot Benoît B. The fractal geometry of nature / Benoît B. Mandelbrot. — San Francisco: W. H. Freeman, 1982. — С. 461.
- ↑ Pietsch M., Aguirre Dávila L., Erfurt P. Spiral Form of the Human Cochlea Results from Spatial Constraints // Scientific Reports. — 2017. — № 7 (7500). — С. 1.
- ↑ Lorenz Edward N. Deterministic Nonperiodic Flow / Edward N. Lorenz // Journal of the Atmospheric Sciences. — 1963. — № 2. — Vol. 20. — P. 130—141. Архивировано 29 мая 2020 года.
- ↑ Короновский Н. В. Основы геологии / Н. В. Короновский, А. Ф. Якушова. — М.: Высшая Школа, 1991. — С. 416.
- ↑ Болл Ф. Закономерности в природе: самотканый ковёр. Формы / Ф. Болл. — М.: Издательство студии Артемия Лебедева, 2025. — С. 155.
- ↑ Болл Ф. Закономерности в природе: самотканый ковёр. Формы / Ф. Болл. — М.: Издательство студии Артемия Лебедева, 2025. — С. 61.
- ↑ Болл Ф. Закономерности в природе: самотканый ковёр. Формы / Ф. Болл. — М.: Издательство студии Артемия Лебедева, 2025. — С. 295.
- ↑ Ye Y. How animals get their stripes and spots (англ.). CU Boulder Today (8 ноября 2023). Дата обращения: 21 сентября 2025.
- ↑ 11,0 11,1 Михайлова А. С. №. 4 (38) // Бионические паттерны в архитектуре и дизайне / А. С. Михайлова, Н. М. Надыршин. — Известия Казанского государственного архитектурно-строительного университета, 2016. — С. 96—103.
- ↑ Brewster D. Treatise on the kaleidoscope. — Edinburgh: Archibald Constable & Co, 1819. — С. 1—8. — 89 с.
- ↑ Ciaccio E. J., Dunn S.M., Akay M. 4 of 4: Review of applications // Biosignal pattern recognition and interpretation systems.. — IEEE Engineering in Medicine and Biology Magazine, 1994. — Т. 13, Issue 2. — С. 269–273.
- ↑ Веселова И. Паттерны согласованной реальности: полихромное вязание // Первичные знаки / Назначенная реальность. — 2017. — С. 195–228.
- ↑ Bakumenko M. N. №. 2 // Вопросы теории паттерна в музыке ХХ века // Проблемы музыкальной науки / Music Scholarship. — 2011. — С. 205–213.