Простое число

Простые числа (до 100)

Просто́е число́ — натуральное число больше единицы, которое делится только на два числа: на единицу и на само себя.

В современной арифметике натуральные числа классифицируются на три категории:

К первой категории относится только число $1$, имеющее лишь один делитель.

Вторую категорию составляют числа с двумя делителями: единицей и самим собой. Такие числа именуются простыми.

Третья категория включает числа, обладающие более чем двумя делителями, и они называются составными.

Число $1$ было выделено из класса простых чисел, к которому его ранее относили, поскольку некоторые теоремы о простых числах не применимы к нему. Чтобы избежать необходимости каждый раз уточнять, что число $1$ является исключением в таких случаях, его выделили в отдельный класс.

Число $2$ — самое маленькое простое число и единственное чётное среди них. Следующее чётное число — $4$, которое уже является составным, так как делится на $1;2;4$, что означает наличие более двух делителей.

Количество простых, как и составных чисел бесконечно. Характеристики и свойства простых чисел изучает теория чисел (аналитическая и аддитивная теории чисел) .

История

У пифагорейцев возникло понятие простого числа, хотя Платон не употреблял этот термин. Аристотель называл простые числа «пифагорейским открытием» и использовал сам термин.

Теорема о бесконечности множества простых чисел известна как теорема Евклида (IX книга математического труда «Начала») — самая известная теорема о простых числах. Некоторые источники указывают, что она была знакома ещё Платону, который жил за 25 лет до рождения Евклида. Математик О. Беккер предполагает, что эта теорема возникла в эпоху Пифагора, жившего в VI—V веках до нашей эры. Л. Эйлер и другие учёные после него предоставили свои доказательства этой теоремы.

Один из самых первых и наиболее известных способов нахождения простых чисел принадлежит древнегреческому математику, астроному и географу Эратосфену (273—194 годы до нашей эры). Метод носит название решета Эратосфена.

Арабская математика

Около 1000 года нашей эры выдающийся исламский математик Ибн аль-Хайтам, известный также как Альхазен (965—1040 годы), выдвинул гипотезу, что если (p — 1)! ≡ −1 (mod p), то число p является простым. Однако он не смог доказать это утверждение.

Другой выдающийся исламский учёный, Ибн аль-Банна аль-Марракуши (1256—1321 годы), заметил, что процесс решета Эратосфена можно значительно ускорить, если учитывать только простые делители, которые не превышают квадратный корень из верхней границы диапазона поиска простых чисел.

Итальянский математик Фибоначчи (1170 — 1250 годы) перенёс инновации из исламской математики в Европу. Его книга «Liber Abaci» (1202 год) была первой, в которой описано пробное деление для проверки простоты с использованием делителей с точностью до квадратного корня.

Прорыв в построении теории простых чисел

В 1603 году итальянский математик Катальди издал «Трактат о совершенных числах». В этом труде он доказал, что числа вида $2^{p}-1$ при $p=17$и $p=19$ — простые. Для этого он использовал метод перебора возможных простых делителей.

В этот же период жил и работал Марен Мерсенн (1588—1648 годы). Его величайшим вкладом в математику стал трактат «Физико-математические размышления» (1644 год), где впервые появились знаменитые простые числа, позже названные его именем.

Леонард Эйлер, живший с 1707 по 1783 год, также уделял большое внимание изучению свойств простых чисел. Он составил таблицу всех простых чисел от $1$ до $100000$ и разработал формулы, которые позволяли находить такие числа.

Российские учёные

В XIX веке российский учёный Пафнутий Львович Чебышёв внёс свой вклад в развитие теории простых чисел. В 1848 году он представил Академии наук Санкт-Петербурга работу «О функции, определяющей все простые числа, меньшие заданного предела». В этом исследовании он изучал функцию, которая каждому положительному целому числу сопоставляет количество простых чисел, не превышающих это число. В 1850 году П. Л. Чебышёв доказал, что между числами «n» и «2n — 2» (где «n > 3») всегда находится хотя бы одно простое число.

Среди других выдающихся математиков стоит отметить российского священника и математика И. М. Первушина (1827—1900 годы). Иван Первушин доказал, что число $2^{61}-1=2305843009213693851$ является простым. Примечательно, что показатель степени $61$ не был включён в список Мерсенна, однако полученное число действительно оказалось простым. Таким образом, список чисел Мерсенна был дополнен новым элементом, что расширило представления о простых числах.

В 1742 году прусский и российский математик Христиан Гольдбах, работавший в Петербургской академии наук, выдвинул гипотезу о том, что любое нечётное число, превышающее $5$, можно представить в виде суммы трёх простых чисел. Это предположение, что стало важным вкладом в теорию чисел. Академик Иван Матвеевич Виноградов, выдающийся русский математик, в 1937 году разработал инновационный метод в аналитической теории чисел, известный как метод Виноградова. С его помощью учёный получил асимптотическую формулу для количества представлений нечётного числа в виде суммы трёх простых чисел.

Современные исследования

В 1996 году Джордж Вольтман, родившийся в 1957 году, инициировал проект GIMPS, направленный на поиск чисел Мерсенна в интернете. С момента основания и до 2018 года основным инструментом для тестирования этих чисел служил алгоритм Лукаса-Лемера. Этот метод, предназначенный для проверки простоты чисел Мерсенна, особенно эффективен на бинарных вычислительных системах. 21 декабря 2018 года благодаря усилиям GIMPS было обнаружено самое большое известное на тот момент простое число $2^{82589933}-1$, состоящее из 24 862 048 цифр.

11 октября 2024 года в Дублине графический процессор NVIDIA A100 выявил вероятность того, что число M136279841 является простым. На следующий день, 12 октября, другой процессор, NVIDIA H100, находящийся в Сан-Антонио (США), подтвердил эту гипотезу с помощью специализированного теста Лукаса-Лемера.

Бесконечность ряда простых чисел

Теорема о бесконечность ряда простых чисел (теорема Евклида) гласит: «Не существует наибольшего простого числа», так как если бы простых чисел было конечное множество, то среди них обязательно нашлось бы наибольшее. В арифметике доказывается, что за каждым простым числом, независимо от его величины, следуют другие простые числа. В доказательстве используют метод от противного.

Предположим, что существует самое большое простое число $p$. Рассмотрим произведение всех простых чисел, начиная с $2$ и заканчивая $p$, и прибавим к этому произведению единицу. Обозначим полученное число как N = 2 $\cdot$ 3 $\cdot$ 5 $\cdot$ … $\cdot$ p + 1. Очевидно, что N больше, чем $p$. Число N может быть либо простым, либо составным. В первом случае теорема доказана: мы нашли простое число N, которое больше предполагаемого наибольшего простого числа $p$, и наше предположение о существовании такого числа оказалось неверным.

Если же N является составным числом, то у него должен быть хотя бы один простой делитель. Однако ни одно из простых чисел $2;3;5;...;p$ не может быть этим делителем, так как при делении N на любое из этих чисел остаток всегда равен $1$. Теорема о бесконечности простых чисел имеет и прямое доказательство.

Определение простоты чисел

Алгоритм, который при вводе числа определяет, является ли оно простым, называется тестом простоты или проверкой простоты. Если алгоритм подтверждает, что число не является составным, это называется истинным тестом простоты. Некоторые тесты простоты:

• метод пробных делений;
• тест Поклингтона;
• тест простоты Миллера-Рабина;
• вероятностный тест простоты Соловея-Штрассена;
• полиномиальный критерий простоты AKS.

Таблицы простых чисел

Решето Эратосфена (анимация)

Когда выяснилось, что натуральный ряд чисел содержит бесконечное количество простых чисел, встал вопрос о том, как их выделить среди других чисел. Первую попытку решения этой задачи предпринял Эратосфен.

Решето Эратосфена

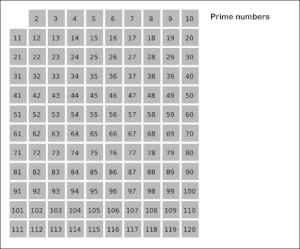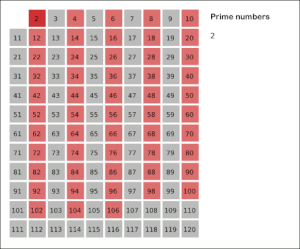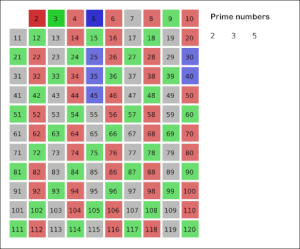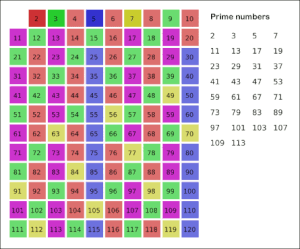
Для создания таблицы простых чисел, не превышающих заданного целого N, можно использовать метод, известный как решето Эратосфена. Этот метод заключается в следующем. Сначала выписываются числа от 1 до N (ряд (1)). Первым числом, большим $1$, является $2$. Так как $2$ делится только на $1$ и само на себя, оно является простым. Из ряда (1) вычеркиваются все числа, кратные $2$, за исключением самого $2$. Следующее число после $2$, которое не вычеркнуто, — это $3$. Поскольку $3$ не делится на $2$ (иначе оно было бы вычеркнуто), оно является простым. Затем из ряда (1) вычеркиваются все числа, кратные $3$, за исключением самого $3$. Первое число после $3$, которое осталось не вычеркнутым, — $5$. Так как $5$ не делится ни на $2$, ни на $3$, оно также является простым. Этот процесс продолжается. Когда все числа, кратные простых чисел, меньших данного простого числа $p$, уже вычеркнуты, все оставшиеся числа, меньшие $p^{2}$, будут простыми. Это объясняется тем, что любое составное число a, меньшее $p^{2}$, уже вычеркнуто как кратное его наименьшего простого делителя, который меньше $p$. Отсюда следует:

1. При вычёркивании кратных простого числа $p$, начинать следует с $p^{2}$.

2. Таблица простых чисел, не превышающих N, считается составленной, когда вычеркнуты все составные числа, кратные простых чисел, не превышающих ${\sqrt {N}}$.

В эпоху Эратосфена писали на восковых табличках. Вместо того чтобы вычёркивать числа, в них делали проколы, превращая дощечку в подобие решета. Этот метод получил название «эратосфеново решето». Несмотря на свою кажущуюся простоту, идея Эратосфена, в усовершенствованной форме, применяется и сегодня для решения сложных задач в теории чисел.

Графическая интерпретация решета Эратосфена

Графическая интерпретация решета Эратосфена, представляющая собой одно из приложений параболы, демонстрирует необычный метод фильтрации натуральных чисел. Этот метод известен как решето Матиясевича — Стечкина, или визуальное сито для простых чисел.

Рассмотрим модель, где строится парабола $y=x^{2}$, а на осях координат отмечаются целые положительные числа. Натуральный ряд размещается на оси ординат. На графике отмечаются точки с целочисленными координатами и соединяются отрезками: каждая точка одной ветви параболы соединяется со всеми точками другой ветви. В результате получается множество хорд с концами в точках (a; $a^{2}$) и (b; $b^{2}$), где a и b принимают значения $2;3;4$ и так далее. Каждая из этих хорд пересекает ось ординат в точке (0; ab). Очевидно, что произведение ab является составным числом. Если провести все такие отрезки, то из натурального ряда будут исключены составные числа, и останутся только простые.

Решето Аткина

Решето Аткина — современный и эффективный алгоритм для нахождения всех простых чисел до заданного значения. Оно представляет собой усовершенствованную версию древнего решета Эратосфена. Алгоритм Аткина выполняет предварительную работу, после чего исключает числа, которые кратны квадрату простого числа. Решето было разработано А. Аткиным и Д. Бернштейном.

Алгоритм его использования основан на применении квадратичных форм. По оценке авторов алгоритм имеет асимптотическую сложность O. Ранее были известны столь же асимптотически быстрые алгоритмы, но они требовали существенно больше памяти.

«Охотники» за большими простыми числами

До конца XVI века математика не знала никаких иных средств для определения простоты или непростоты числа а, кроме непосредственных проверок делением его на все простые числа, меньшие или равные а, или составления «решета».

В течение последующих веков математики Ферма, Лейбниц, Ламберт, Эйлер и Гаусс разработали несколько методов для упрощения этой проверки. Во времена Эйлера (1772 год) наибольшим известным простым числом было: $2^{31}-1=2147483647$. В 1883 году сельский священник Иван Михеевич Первушин, доказал, что число $2^{61}-1=2305843009213693951$ — простое.

До 1950 года осуществление поиска простых чисел вида $2^{n}-1$ с использованием доступных вычислительных средств было затруднительно. 30 января 1952 года, благодаря электронной вычислительной машине, было установлено, что число $2^{521}-1$, состоящее из 157 знаков, является простым. В октябре того же года были найдены два простых числа: $2^{220}-1$ и $2^{228}-1$, которые насчитывают от 700 до 750 цифр.

До появления электронных вычислительных машин самым успешным «охотником за большими простыми числами» был математик Деррик Норман Лемер (1867—1938 годы). В 1932 году он доказал, что число $2^{257}-1$ является составным. Используя доступные тогда вычислительные инструменты, Лемер потратил целый год на решение этой задачи. Его сын, Г. Д. Лемер, столь же увлечённый поисками больших простых чисел, как и его отец, в январе 1952 года наблюдал, как электронная вычислительная машина выполнила годовой объём работы прежних устройств всего за 48 секунд, подтвердив результат, полученный его отцом двадцать лет назад. К концу 1957 года наибольшим известным простым числом считалось число $2^{281}-1$.

В настоящее время графические процессоры способны применяться не только в сфере искусственного интеллекта, но и в различных областях фундаментальной науки. Люк Дюрант, ранее работавший в NVIDIA и активно участвующий в проекте GIMPS, обнаружил самое большое простое число (по состоянию на 2025 год), состоящее из 41 024 320 цифр. Это 52-е число Мерсенна по счёту, и оно на 16 миллионов цифр превышает предыдущий рекорд. Новое число получило название M136279841. Чтобы его получить, нужно возвести $2$ в степень 136 279 841, а затем вычесть единицу.

Взаимно простые числа

Числа, у которых нет общих делителей, кроме единицы, называются взаимно простыми. Их наибольший общий делитель равен единице, что обычно обозначают символом НОД (a, b) = 1.

Число $1$ является взаимно простым с любым целым числом. Если $p$ — простое число, тогда все числа от $1$ до $p-1$ являются взаимно простыми к числу $p$.

Основные теоремы, связанные с простыми числами

Приведём (без доказательства) основные теоремы о простых числах.

Основная теорема арифметики

Одной из наиболее перспективных концепций современной математики является подход к изучению математических объектов через их разложение на более простые составляющие. Эта идея зародилась в контексте исследования натуральных чисел и получила своё первоначальное выражение в виде так называемой «основной теоремы арифметики».

Частный случай основной теоремы арифметики был изложен и обоснован Евклидом в VIII книге его труда «Начала», написанного в III веке до нашей эры. Впервые же в полной общности эта теорема была сформулирована и доказана Карлом Фридрихом Гауссом в 1801 году в его знаменитом произведении «Арифметические исследования». Она формулируется следующим образом: каждое натуральное число n > 1 можно представить в виде произведения конечного числа простых чисел и такое представление единственно с точностью до порядка следования простых сомножителей.

Малая теорема Ферма

Малая теорема Ферма утверждает, что $a^{p-1}$ ≡ 1 (mod p) для всякого целого a, не делящегося на p, или, что эквивалентно, $a^{p}$ ≡ a (mod p) для всякого целого a, где p простое число.

Иными словами: если — р простое число и а — число, не делящееся на р, то $a^{p-1}$ делится на $p$. Это утверждение было сообщено Пьером Ферма без доказательства в письме Френиклю де Бесси от 18 октября 1640 года. На Пьера Ферма обнаруженная им закономерность произвела очень большое впечатление. «Меня озарило ярким светом», писал он, сообщая о теореме.

Теорема Эйлера

Напомним, что для любого натурального числа $m$ через $\varphi (m)$ обозначается количество натуральных чисел, не превосходящих m и взаимно простых с m. Функция $\varphi$, называемая функцией Эйлера, обладает следующим свойством мультипликативности (вытекающим из китайской теоремы об остатках): если $m_{1}$ и $m_{2}$ взаимно простые натуральные числа, то $\varphi (m_{1}m_{2})=$$\varphi (m_{1})\varphi (ma_{2})$. Если $m=p$ простое число, то $\varphi (m)$ = p − 1; если m = $p^{n}$, то $\varphi (m)$ = $p^{n}$ — $p^{p-1}$

Теорема Эйлера (сравнение Эйлера) утверждает, что $a^{\varphi (m)}\equiv 1{\pmod {m}}$ для всякого целого a, взаимно простого с $m$. Это, очевидно, является обобщением малой теоремы Ферма.

Китайская теорема об остатках

Китайская теорема об остатках (КТО) — это математическое утверждение, позволяющее определить остаток от деления неотрицательного целого числа ($x$) на наименьшее общее кратное нескольких взаимно простых натуральных чисел, если известны остатки от деления ($x$) на эти числа. Эта теорема находит широкое применение в системе остаточных классов (СОК), которая представляет числа с помощью остатков от деления на другие числа. СОК является ключевой концепцией, связанной с практической реализацией КТО.

Применение простых чисел в криптографии

В современном мире одной из ключевых задач в области математики остается поиск закономерностей в распределении простых чисел. Этот интерес обусловлен тем, что простые числа являются основой для современной криптографии, что делает их важным элементом повседневной жизни. Практически каждый процесс аутентификации, будь то банковские операции или регистрация телефона в сети, не обходится без использования простых чисел.

Для каждого простого числа существуют первообразные корни. Если выбрать простое число и первообразный корень, можно зашифровать сообщение. Для этого его записывают в виде вычета по модулю данного простого числа, а затем возводят первообразный корень в степень, равную этому вычету. Полученный результат, который является новым вычетом, и будет зашифрованным сообщением. Оно передается абоненту. Этот процесс довольно прост. Однако обратная задача — восстановление исходного сообщения по зашифрованному, которое мог перехватить злоумышленник, — значительно сложнее. Она становится тем труднее, чем больше исходное простое число. Для её решения даже с использованием современных технологий может потребоваться так много времени, что сама задача утратит актуальность.