Диаметр

Диаметр
⌀
Изображение
◄ ⋼ ⋽ ⋾ ⋿ ⌀ ⌁ ⌂ ⌃ ⌄ ►
Характеристики
Название	diameter sign
Юникод	U+2300
HTML-код	⌀ или ⌀
UTF-16	0x2300
URL-код	%E2%8C%80

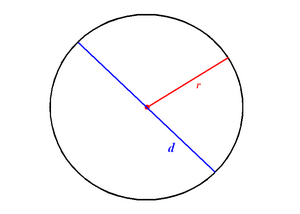
Диа́метр (от фр. diamètre из лат. diametrus из др.-греч. διάμετρος — «поперечник») — отрезок, соединяющий две точки на окружности и проходящий через её центр, а также длина этого отрезка. В обобщённом понимании диаметром фигуры называется максимальное расстояние между её точками или точная верхняя грань всевозможных расстояний, если максимального не существует.

Математические основы

Геометрическое определение

Диаметр представляет собой хорду окружности, проходящую через её центр и обладающую наибольшей возможной длиной среди всех хорд данной окружности. Данное свойство определяет диаметр как ключевой элемент геометрических построений и вычислений.

В теории конических сечений диаметром называется любая прямая, проходящая через центр фигуры. Для эллипса диаметр соединяет две точки на нём через центр, при этом наибольший и наименьший диаметры образуют большую и малую оси соответственно. У параболы диаметры представляют собой прямые, параллельные оси симметрии, а у гиперболы — прямые, проходящие через середины параллельных хорд.

Метрические свойства

Основное метрическое свойство диаметра заключается в равенстве удвоенному радиусу окружности. Соотношение $d=2r$ является базовым для геометрических расчётов, связанных с окружностями и сферами.

В метрических пространствах диаметр — это точная верхняя грань всех расстояний между парами точек этого множества. Математически обозначается как $\operatorname {diam} (S)=\sup \,\{d(x,y):x,y\in S\}$, где $d(x,y)$ — расстояние между точками x и y в заданной метрике. Данное определение позволяет распространить понятие диаметра на произвольные геометрические объекты и абстрактные множества.

Диаметр обладает свойством монотонности: для любых множеств $A\subseteq B$ выполняется неравенство $\operatorname {diam} (A)\leq \operatorname {diam} (B)$. Диаметр объединения множеств не превышает суммы их диаметров плюс расстояние между ними, что лежит в основе оценок в геометрической теории меры.

Связь с радиусом

Диаметр и радиус находятся в строгой математической зависимости, где радиус равен половине диаметра. Данное соотношение справедливо для евклидовой метрики и окружностей, тогда как для других геометрических объектов применяется теорема Юнга, устанавливающая более общие неравенства.

Диаметр

Этимология и терминология

• Языковые корни

Термин происходит от древнегреческого др.-греч. διάμετρος (diametros), образованного сочетанием предлога др.-греч. διά (dia) — «через, поперёк» и существительного др.-греч. μέτρον (metron) — «мера, измерение». Этимология отражает геометрическую суть понятия как измерения, проходящего через центр фигуры.

• Развитие понятия

В современной математической терминологии понятие диаметра применяется в метрических пространствах, теории графов, топологии и других разделах математики, выходя за пределы классической геометрии окружности.

Символика и обозначения

• Символ диаметра

В технических чертежах и спецификациях диаметр обозначается символом ⌀, представленным в стандарте Юникод под кодом U+2300 DIAMETER SIGN. Символ входит в блок Miscellaneous Technical и используется как префикс или суффикс к числовому значению.

• Кодирование и ввод

Символ диаметра вводится следующими способами:

• в HTML как ⌀ или ⌀
• в Microsoft Word комбинацией 2300 + Alt+X;
• в системах Windows через Alt+8960;
• в операционных системах на базе X Window System используется последовательность Ctrl+⇧ Shift+u 2300Пробел.
• Альтернативные обозначения. При недоступности специального символа применяются альтернативные обозначения: символ пустого множества ∅ (\U+2205), латинская буква Ø или сокращения DIA, Φ. В системе AutoCAD используется команда %%c для вставки символа диаметра.

Геометрические конструкции

• Построение диаметра

Построение диаметра окружности выполняется при помощи циркуля и линейки как перпендикуляр к произвольной хорде, проходящий через её середину. Пересечение двух диаметров определяет положение центра окружности.

• Диаметр как хорда

Из всех хорд окружности диаметр является самой длинной. Любой отрезок, не проходящий через центр, имеет длину меньше диаметра.

• Перпендикулярные диаметры

Два диаметра одной окружности всегда пересекаются в центре под прямым углом, образуя систему взаимно перпендикулярных осей симметрии окружности.

Специальные типы диаметров

Диаметры элипса

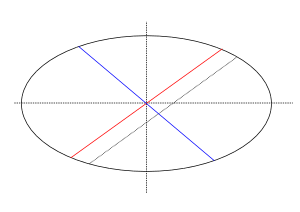
Сопряжённые диаметры эллипса

$r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}$

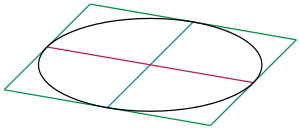
Математическое определение сопряжённых диаметров эллипса основывается на взаимном расположении геометрических элементов: для каждой пары диаметров существует зависимость, при которой срединные точки хорд, параллельных первому диаметру, лежат на втором диаметре. Данное свойство характеризует фундаментальную связность внутренней структуры эллипса.

Сопряженные диаметры

Касательные прямые, проведённые в точках пересечения диаметра с границей эллипса, обладают свойством параллельности относительно сопряжённого диаметра. Совокупность четырёх касательных образует описанный параллелограмм вокруг эллипса.

$k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}$

Фокальные радиусы представляют собой расстояния от произвольной точки эллипса до его фокусов. Радиус-вектор от центра эллипса до точки на его границе определяется выражением, где $\phi$ обозначает угол между радиус-вектором и большой полуосью, параметры $a$ и $b$ соответствуют большой и малой полуосям.

Диаметры гиперболы

Диаметр гиперболы определяется как прямая, являющаяся геометрическим местом середин хорд с заданным направлением. Все диаметры гиперболы проходят через её центр. Действительная и мнимая оси составляют главные диаметры — единственную взаимно сопряжённую и ортогональную пару. Каждому направлению параллельных хорд соответствует свой диаметр.

Гипербола характеризуется специфическими геометрическими свойствами диаметров, отличающимися от свойств замкнутых конических сечений. Угловые коэффициенты параллельных хорд и соответствующего диаметра связаны соотношением, где $a$ и $b$ являются параметрами гиперболы.

Гиперболы с ортогональными асимптотами демонстрируют специальное свойство: их сопряжённые диаметры сохраняют взаимную перпендикулярность. При отражении относительно асимптоты диаметр трансформируется в сопряжённый диаметр отражённой гиперболы.

Обобщения понятия

• Диаметр множества

В метрических пространствах диаметр множества определяется как точная верхняя грань расстояний между всеми его точками:

$\operatorname {diam} (S)=\sup \,\{d(x,y):x,y\in S\}$.

• Многомерные пространства

Для n-мерного гиперкуба со стороной $s$ диаметр вычисляется по формуле $d=s{\sqrt {n}}$, что соответствует максимальному расстоянию между противоположными вершинами.

• Метрические обобщения

Понятие диаметра распространяется на различные метрические структуры, включая пространства с неевклидовыми метриками и дискретные объекты.

Техническое применение

• Инженерная графика

В технических чертежах символ диаметра служит стандартным обозначением круглых сечений деталей, труб, отверстий и цилиндрических элементов. Корректное указание диаметров необходимо для точности изготовления.

• САПР и автоматизация

Системы автоматизированного проектирования используют алгоритмы для обработки размеров диаметров, обеспечивая автоматическое вычисление связанных параметров и контроль соответствия стандартам.

• Стандарты обозначений

Международные стандарты технического черчения регламентируют применение символа диаметра, обеспечивая однозначность понимания технической документации.

Специальные области применения

• Гидравлический диаметр

Гидравлический диаметр применяется в гидродинамике для характеристики некруглых каналов и вычисляется как учетверённое отношение площади сечения к смоченному периметру.

• Теория графов

Диаметр графа определяется как максимальное расстояние между любыми двумя вершинами, измеряемое количеством рёбер в минимальном пути.

• Астрономические измерения

В астрономии угловой диаметр небесных объектов позволяет определять их истинные размеры при известном расстоянии до объекта.

Исторические аспекты

Античные вычисления

Эратосфен около 240 г. до н. э. вычислил диаметр Земли, применив геометрические методы — классический пример практического применения геометрии.

Метод основывался на наблюдении теней в разных точках. В полдень летнего солнцестояния в Сиене солнце освещало дно колодцев (зенитное положение), а в Александрии вертикальные предметы отбрасывали тень под углом 7,2°.

Используя расстояние между городами (800 км) и пропорциональные вычисления, Эратосфен определил длину окружности Земли — около 40 000 км. Диаметр составил примерно 12 700 км.

Развитие концепции

Понятие диаметра эволюционировало от геометрического термина до фундаментального концепта математики с широким применением в науке.

В Средневековье арабские математики использовали диаметр в астрономии, в эпоху Возрождения он применялся в искусстве и перспективе. XIX век ознаменовался появлением неевклидовых геометрий, показавших новое поведение диаметра в искривлённых пространствах.

Современность отмечена широким применением концепции в цифровых технологиях — графике, навигации, томографии. Квантовая физика исследует диаметры орбиталей, астрофизика — радиусы горизонтов событий чёрных дыр.

Перспективы развития связаны с применением искусственного интеллекта для распознавания объектов и квантовые вычисления в многомерных пространствах.

Литература

• Том XА. Десмургия — Домициан // Энциклопедический словарь Брокгауза и Ефрона / под ред. К. К. Арсеньева и Ф. Ф. Петрушевского. — СПб.: Семеновская Типолитография, 1893. — 499 с.
• Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых третьего порядка. — М.: Физматлит, 1961. — 263 с.
• Этимологический словарь русского языка = Russisches etymologisches Wörterbuch : в 4 т. / авт.-сост. М. Фасмер ; пер. с нем. и доп. чл.‑кор. АН СССР О. Н. Трубачёва, под ред. и с предисл. проф. Б. А. Ларина [т. I]. — Изд. 2-е, стер. — М. : Прогресс, 1986—1987.