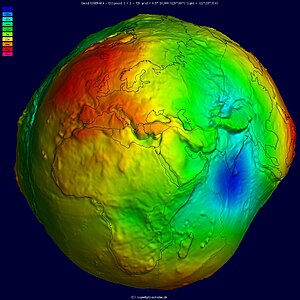
Геоид

Волнистость геоида

Гео́ид — уро­вен­ная по­верх­ность, об­ра­зо­ван­ная по­верх­но­стью Ми­ро­во­го океана в со­стоя­нии по­коя и рав­но­ве­сия, про­дол­жен­ной под ма­те­ри­ка­ми. По­тен­ци­ал тя­же­сти равен сум­ме по­тен­циа­ла тя­го­те­ния и цен­тро­беж­но­го по­тен­циа­ла. Вектор си­лы тя­же­сти об­ра­зу­ет от­вес­ную ли­нию, ко­то­рая пер­пен­ди­ку­ляр­на по­верх­но­сти геоида.

Геоид не является правильной стереометрической фигурой. Его поверхность приблизительно совпадает с поверхностью мирового океана и продолжается на материковой части нашей планеты. «Высота над уровнем моря» какого-либо пункта на материке отсчитывается от этой поверхности.

История

Народы Древней Индии убеждены, что формой Земли являлась — полусфера, опирающаяся на спины четырёх гигантов — слонов. Слоны стоят на спине огромной черепахи, которая обитает в море молока. Все существа при этом обвиты чёрной коброй Шешу, имеющей тысячи голов, подпирающих Вселенную. На территории Древней Греции было принято считать, что планета является выпуклым диском, напоминающим щит воина. По медному небосводу двигается Солнце, суша со всех сторон окружена водой — Океаном.

Жители древней Японии предписывали планете кубическую форму. Для землетрясений, которые являлись частым явлением на территории государства, было найдено интересное объяснение. Землетрясения, по их поверьям, вызывались буйствами огнедышащего дракона, обитающего в глубинных недрах Земли. В Китае планета виделась плоским прямоугольником, по всем углам которого расположены четыре опоры. Итак, колонны подпирают выпуклый купол небес. Одна из них когда-то давно была повреждена чудищем — драконом, и это привело к тому, что Земля постоянно кренится на восток, а небо имеет уклон на запад. Теория доступно объясняла передвижения небесных светил и течение рек, которое направлено на восток.

Ацтеки и майя были уверены, что форма Земли — квадратная. В центре фигуры произрастает Первоначальное Древо, по углам — ещё по одному из деревьев, каждое из которых имеет своё обозначение. До Земли существовали лишь Небо и Вода, к созданию суши приложили руку боги, главным деятелем стал Кетцалькоатль.

Корабельные путешествия, появление подробных карт позволило ещё в Средневековье сделать выводы, что Земля имеет шарообразную форму. Именно в этот исторический период было установлено, что все планеты Солнечной системы, в том числе и наша, вращаются вокруг Солнца. Благодаря изысканиям всем известных Николая Коперника, Джордано Бруно, Галилео Галилея. В 1873 году впервые введено понятие «геоид». Его автором является физик и математик Иоганн Листинг. Данный термин введён для обозначения формы планеты, которая максимально приближена к эллипсоиду вращения.

Описание

Поверхность геоида, в отличие от физической поверхности Земли, гладкая, но тоже довольно неправильная. Если сравнивать с телом ещё более правильной формы — эллипсоидом, то геоид имеет и впадины (на юге Индии 160 м, на Кубе 97 м) и выпуклости (в Папуа 120 м, в Западной Африке 136 м).

Как геоид, так и квазигеоид, не являются телами правильной формы, не имеют простого математического описания и не могут быть использованы для задания системы координат. Землю необходимо ещё больше «сгладить». Поэтому для задания на Земле системы координат геоид аппроксимируют эллипсоидом вращения, то есть фигурой, образованной путем вращения эллипса (плоской фигуры) вокруг малой его оси. Эллипс представляет собой сжатую окружность.

Аппроксимация с помощью сферических функций

При алгоритмизации перспективных задач судовождения дополнительно предлагается использовать свойство локальности сплайнов с частичной возможностью организации расчётов по явным формулам в уникальных случаях. При этом спутниковая информация подвергается сглаживанию, что может быть важным, когда в измерениях радионавигационных параметров присутствует хаотичная погрешность. Локальную интерполяцию организует простая математическая перестановка сплайновых линейных функционалов с навигационными параметрами.

На основе разработанного гибридного алгоритма выполнено компьютерное моделирование фрагмента электронного профиля геоида. Геометрическая интерпретация вычислительных реализаций алгоритма гибридной сплайн-аппроксимации апробируется построением на дисплее компьютера электронных перспектив геоида в различных ракурсах в мультипликативном режиме с целью демонстрации работоспособности предлагаемого алгоритмизированного аппарата. Графическое воспроизведение каждой изолинии геоидной поверхности означает демонстрацию алгоритмической возможности вычисления мгновенного значения навигационной функции в каждой точке синтезированной линии с последующей пиксельной визуализацией битовой карты матрицы изолинии как частного случая навигационной изоповерхности.

Квазигеоид

В XXI веке на акватории Мирового океана геоид с высокой точностью (до 0,1—0,3 м по высоте) изучают методом спутниковой альтиметрии, измеряя расстояния от спутника до подспутниковых точек на поверхности морей и океанов. Эти измерения показали, что невозмущенная морская поверхность не везде совпадает с уровенной поверхностью потенциала силы тяжести: в отдельных районах отклонения по высоте достигают ± (1,5—2) м. Поэтому при теоретически строгом подходе под геоидом понимают фигуру Земли, ограниченную уровенной поверхностью потенциала силы тяжести, проходящей через начало отсчета высот, совпадающее с некоторым средним уровнем Мирового океана.

При изучении фигуры геоида на суше метод спутниковой альтиметрии не работает, а другие методы космической геодезии дают недостаточную точность определения его поверхности. Для того чтобы изучить фигуру геоида по наземным измерениям с высокой точностью, необходимо силу тяжести измерять непосредственно на его поверхности, что не осуществимо. Следовательно, как доказал известный советский ученый Михаил Сергеевич Молоденский, изучить фигуру геоида с высокой точностью по наземным измерениям невозможно. По результатам комплекса наземных астрономо-геодезических и гравиметрических измерений теоретически безупречно может быть определена другая вспомогательная поверхность, получившая название поверхности квазигеоида, которая незначительно отклоняется от поверхности геоида: в равнинной местности на 2— 4 см, а в горах — не более 2 м. На морях и океанах поверхности геоида и квазигеоида полностью совпадают.

Аномалии

Гравитационные аномалии, возникающие из-за неравномерного распределения плотности в недрах Земли, приводят к изменениям в высоте геоида. Таким образом, исследования геоида позволяют глубже разобраться в внутреннем строении нашей планеты. Согласно расчетам, геоидальная характеристика утолщенной земной коры, например, возникающей в результате тектонических процессов, связанных со столкновением континентов, проявляется как положительная. Это контрастирует с тем, что можно было бы ожидать, если бы утолщение затрагивало всю литосферу.

Изменение уровня воды

Изменения высоты поверхности геоида происходят очень медленно и становятся заметными только в геологических масштабах времени. Это обстоятельство позволяет принять топографию геоида в качестве отсчетной уровенной поверхности Мирового океана, на которую накладываются и от которой отсчитываются все регистрируемые изменения уровня воды разных масштабов.

Процессы, приводящие к изменениям уровня, сильно разнятся по времени (периодичность и продолжительность), месту и масштабам воздействия, приводя в одних случаях к местным и кратковременным колебаниям, в других — проявляются на всей акватории Мирового океана на протяжении многих сотен и тысяч лет. Кратковременные колебания уровня происходят при сохранении общего объёма воды в Мировом океане и отражают периодические перераспределения воды от одних районов к другим. Такие колебания происходят под влиянием ветра, атмосферного давления, осадков, испарения, приливов, пресного стока, колебаний плотности воды, подводного вулканизма, сейсмических подвижек океанической земной коры (волны цунами). Временные масштабы таких изменений — от десятков секунд и минут до года и нескольких лет.

См. также

• Датум
• Фигура Земли
• Земной эллипсоид
• Уровенная поверхность
• Квазигеоид