Частота

Частота
Частота
Размерность	T−1
Единицы измерения
СИ	Гц

Частота́ — физическая величина, определяющая степень периодичности явлений, количество повторяющихся событий в единицу времени, выраженное через отношение их числа к временному интервалу. Обозначается с использованием греческой буквы $\nu$ («ню»)^[1].

Единицы измерения частоты

Герц, Генрих Рудольф (1857—1894) — немецкий физик, один из основоположников электродинамики

Для каждой колебательной системы частота ( $\nu$ ) и период (T) являются постоянными. Связь между этими величинами довольно проста — обратное отношение: $\nu$ = ${\frac {1}{T}}$ .

Частота измеряется $[\nu ]$ = с⁻¹= 1/с = Гц.

В Международной системе единиц (СИ) единицу измерения частоты называют «герц» (Гц — русское обозначение; Hz — международное обозначение), названную в честь Генриха Герца, немецкого физика. Частота и время являются одними из наиболее точно измеряемых физических величин^[2].

Частота в науке и технике

Зависимость частоты колебаний от периода

Частота колебаний

Частота колебаний — это скоростная характеристика объектов или систем, определяющая их способность возвращаться в исходное состояние за определённый временной интервал. Это численная мера (количественная оценка) периодических процессов, отражающих количество полных циклов колебаний в единицу времени.

Пример:

маятник математический ( g — ускорение свободного падения [м/c²], l — длина подвеса [м],): $\nu ={\frac {1}{2\pi }}{\sqrt {g \over l}}$

горизонтальный или вертикальный пружинный маятник ( $\kappa$ — жёсткость пружины [кг/с²], $m$ — масса груза [кг]): $\nu ={\frac {1}{2\pi }}{\sqrt {\frac {\kappa }{m}}}$

Частота колебаний также имеет практическое применение в повседневной жизни:

в музыкальной сфере она задаёт высоту звука через частоту волн, восприятие тональности;
в медицинских исследованиях — частота пульса служит показателем состояния организма^[1].

Угловая частота

Угловая частота (круговая частота) представляет собой количество полных колебаний, которые совершены за интервал 2π единиц времени. Найти её можно поформуле: ω = 2πf = π/T, где ω — угловая частота, f — это количество колебаний в секунду, а T — период колебаний. В системе СИ данная величина измеряется в радианах в секунду (рад/с)^[3].

Частота вращения

Вращательная периодичность описывается как количество полных оборотов (N) тела за единицу времени, когда происходит круговое движение^[4].

Вращательное движение

$\upsilon ={\frac {N}{t}}$

Частота вращения является важной характеристикой для различных механических систем. Она измеряется в оборотах в секунду или вращениях в минуту, в зависимости от конкретной ситуации. Частота вращения может быть постоянной или изменяться со временем в зависимости от внешних условий. Эта физическая величина имеет большое значение в технике, физике и других областях науки и техники. Понимание частоты вращения позволяет оптимизировать работу механических устройств и предотвращать их поломки.

Частота переменного тока

Частота переменного тока — число циклов смены направления тока в секунду^[1].

Частота переменного тока измеряется в герцах и обозначается латинской буквой f.
Обычно частота переменного тока в электросети составляет 50 герц (в Европе).
В некоторых странах частота переменного тока может быть 60 герц (в Северной Америке).
Высокие значения могут негативно сказываться на человеческом организме.
Низкая периодичность приводит к мерцающему свету в осветительных приборах.
Частота напрямую влияет на функционирование электронных устройств и систем.
Изменения частоты могут вызывать сбои в работе электроники, снижение её эффективности или стабильности.

Собственная частота колебательного контура

Собственная частота колебательного контура представляет собой частоту, при которой колебания в контуре происходят естественным образом, без внешнего воздействия^[5].

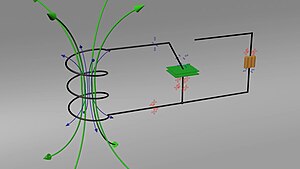
LC-колебательный контур ( $C$ — ёмкость контура, $L$ — индуктивность)

Колебательный контур

\nu ={\frac {1}{2\pi {\sqrt {LC}}}}

1. Характерная для устройства собственная резонансная частота обусловлена взаимодействием индуктивности и ёмкости.

2. Данную частоту можно рассматривать как уникальную характеристику конструкции контура, которая напрямую связана с его параметрами.

3. Вариативность в архитектуре колебательных систем влечёт за собой изменчивость их собственных резонансных значений.

4. Без внешних воздействий собственная частота задаёт основной ритм самовозбуждённых колебаний контура.

5. Изменение параметров контура приводит к изменению его собственной частоты.

Частота излучения

Главным показателем электромагнитного излучения является частота волн^[1]:

основополагающим параметром выступает количество вершин синусоиды), проходящих мимо наблюдателя за единицу времени (секунда);
эта величина именуется как частота излучения и обозначается символом $\nu$ . Для всех электромагнитных волн скорость в вакууме (с) одинакова, то частоту легко определить зная длину волны (λ) по формуле: $\nu ={\frac {c}{\lambda }}$ ;
она определяет скорость периодических изменений волн в электромагнитном поле;
частота, определяющая количество колебаний за секунду, служит ключевым критерием для характеристики свойств электромагнитного излучения;
в различных диапазонах частот (радиоволны, микроволны, инфракрасное и т. д.) частота играет решающую роль в определении их особенностей взаимодействия с материей.

Тактовая частота процессора

Тактовая частота процессора — это скорость, с которой процессор выполняет свои операции. Она измеряется в герцах, что означает количество тактов (или циклов) в секунду. Чем выше тактовая частота, тем быстрее процессор может обрабатывать информацию.

Темп выполнения вычислений в микропроцессоре задаётся его тактовой частотой. Увеличение тактовой частоты способствует ускорению обработки команд и операций, повышая их пропускную способность.Производительность аппаратного устройства (компьютера или другого устройства) непосредственно связана с уровнем его тактовой частоты.

Оптимизация производительности через увеличение тактовой частоты сопряжена с ростом энергопотребления и тепловых нагрузок системы. Современные процессоры функционируют в диапазоне от нескольких гигагерц до многогигагерцевых значений, определяя их скоростную мощь^[6].

Частота в математике

В математике «частота» определяется как безразмерная «встречаемость» — величина, находящаяся в пределе значений от 0 до 1. Используя это понятие для физических периодических процессов, можно экспериментально определять вероятность наступления события (к примеру, прохождения маятника через верхнюю точку) за временной интервал, строго меньший периода колебаний (обозначенного как T), при условии случайного выбора начального момента отсчёта (обозначенного через t) при этом t<T.

Частота в вероятности

В контексте теорий вероятности, показатель относительной частоты занимает ключевое место рядом с фундаментальной мерой - абсолютной вероятностью.

Частота случайного события рассматривается в статистике (устойчивость частот) — закономерность статистического характера, наблюдаемая в массовых случайных явлениях и состоящая в том, что частоты случайных событий близки к их вероятностям^[7].

Существует две категории частоты:

Абсолютная частота — это количество появлений данного события в рамках одного исследования или эксперимента.
Относительная частота — представляет собой отношение числа испытаний, в которых проявилось определенное событие, к общему количеству фактически проведенных испытаний выраженное в процентах. В статистике вероятность вычисляют до опыта, а относительную частоту - после опыта. Относительная частота стабильна: многочисленные эксперименты, выполненные под одинаковыми условиями, подтверждают её неизменную природу — она сохраняет постоянство с небольшими колебаниями вокруг определённой величины^[8].

Частота в статистике

Описание статистических данных делается с помощью частот. В рамках строгого определения математической статистики данные представляются посредством частотных показателей. Здесь частота определяется как отношение количества наблюдаемых единиц или явлений, обладающих определённым свойством (либо попадающих в заданный диапазон), к общему числу наблюдений. Данное определение преимущественно отражает принципы одномерной статистики. При переходе к многомерному анализу подходы существенно меняются, учитывая специфику интерпретации и обработки данных в пространстве большей размерности. Математическая статистика исходит от представлений о тесной взаимосвязи частот с вероятностными характеристиками: при стремлении количества наблюдений к бесконечности, рассматриваемая частота стремится к иной величине, нежели в конечном случае^[9].

Примечания

↑ ^1,0 ^1,1 ^1,2 ^1,3 Частота (рус.). Понятный словарь терминов. Дата обращения: 4 января 2025.
↑ Редакция физических наук. Частота колебаний (рус.). Научно-образовательный портал «Большая российская энциклопедия" (12 октября 2023). Дата обращения: 12 октября 2023.
↑ Редакция физических наук. Угловая частота (рус.). Большая Российсая энциклопедия (19 января 2024). Дата обращения: 10 февраля 2025.
↑ Редакция физических наук. Частота вращения (рус.). Научно-образовательный портал «Большая российская энциклопедия» (22 ноября 2022). Дата обращения: 4 января 2025.
↑ Лобанова Н. Б., Лобанов Ю. А., Зырянова Н. П., Вилисова Е. А., Болячкин А. С. Цели переменного тока. Колебательный контур. — Екатеринбург: Уральский федеральный университет, 2015. — 40 с.
↑ Иевлев, Павел. Что такое тактовая частота процессора (рус.). Журнал о цифровой транформации жизни (21 марта 2023). Дата обращения: 4 января 2025.
↑ Устойчивость частот (рус.). Большая рассийская энциклопедия. Дата обращения: 10 февраля 2025.
↑ Гмурман В. Е. Теория вероятностей и математическая статистика. — М.: Высшая школа, 2003. — С. 24-25. — 479 с. — ISBN 5-06-004214-6.
↑ Орлов А.И. Математика случая. Вероятность и статистика – основные факты. — М.: 2004. — 110 с. / под ред. Я.Ю.Никитина. — М.: МЗ-Пресс, 2004. — С. 97. — 110 с.

[:0-1] 1,0 ^1,1 ^1,2 ^1,3 Частота (рус.). Понятный словарь терминов. Дата обращения: 4 января 2025.

[2] Редакция физических наук. Частота колебаний (рус.). Научно-образовательный портал «Большая российская энциклопедия" (12 октября 2023). Дата обращения: 12 октября 2023.

[3] Редакция физических наук. Угловая частота (рус.). Большая Российсая энциклопедия (19 января 2024). Дата обращения: 10 февраля 2025.

[4] Редакция физических наук. Частота вращения (рус.). Научно-образовательный портал «Большая российская энциклопедия» (22 ноября 2022). Дата обращения: 4 января 2025.

[5] Лобанова Н. Б., Лобанов Ю. А., Зырянова Н. П., Вилисова Е. А., Болячкин А. С. Цели переменного тока. Колебательный контур. — Екатеринбург: Уральский федеральный университет, 2015. — 40 с.

[6] Иевлев, Павел. Что такое тактовая частота процессора (рус.). Журнал о цифровой транформации жизни (21 марта 2023). Дата обращения: 4 января 2025.

[7] Устойчивость частот (рус.). Большая рассийская энциклопедия. Дата обращения: 10 февраля 2025.

[8] Гмурман В. Е. Теория вероятностей и математическая статистика. — М.: Высшая школа, 2003. — С. 24-25. — 479 с. — ISBN 5-06-004214-6.

[9] Орлов А.И. Математика случая. Вероятность и статистика – основные факты. — М.: 2004. — 110 с. / под ред. Я.Ю.Никитина. — М.: МЗ-Пресс, 2004. — С. 97. — 110 с.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]