Длина волны

График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0

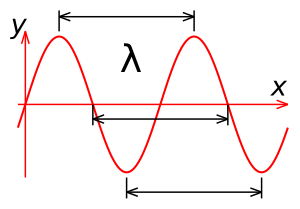
Длина́ волны́ — фундаментальная характеристика волновых процессов, определяемая как расстояние, на которое распространяется волна вдоль линии распространения за время, равное периоду колебания. Длина волны, традиционно обозначаемая греческой буквой $\lambda$ и выражаемая в метрах, является ключевым параметром волны наряду с частотой, амплитудой, начальной фазой, вектором распространения и поляризацией.

Концепция длины волны преимущественно применяется к гармоническим или квазигармоническим (например, затухающим или модулированным с узкой полосой) колебательным процессам в средах с однородными или близкими к однородным свойствами. Тем не менее, это понятие можно экстраполировать и на негармонические, но периодические волновые процессы, содержащие спектр гармоник (элементарных составляющих сложного гармонического колебания). В таком случае длина волны будет соответствовать длине волны основной (наиболее низкочастотной) гармоники в спектральном составе.

Длина волны — пространственный период волнового процесса

Волновое явление представляет собой динамический колебательный процесс, эволюционирующий как в пространстве, так и во времени. В результате этого, физическая величина, характеризующая волну, выражается через специфическую пространственно-временную функцию, зависящую от координат и времени. Волновой процесс может обладать периодичностью, в частности, проявляя гармонический характер.

Проводя аналогию с временным периодом колебаний $T$[с] (интервалом, за который циклический процесс совершает полный оборот) длину волны $\lambda$ [м] можно интерпретировать как пространственную периодичность волнового феномена.

Важно отметить соответствие между круговой частотой $\omega =2\pi f=2\pi /T$ [радиан/с], отражающей скорость изменения фазы колебания в фиксированной точке (или совокупности точек для твёрдого тела), и волновым числом $k=2\pi /\lambda$ [радиан/м], именуемым также «пространственной круговой частотой». Последнее характеризует градиент фазы колебательного процесса между двумя пространственными точками, отстоящими друг от друга на 1 м вдоль направления распространения волны.

Закономерно, что разность фаз колебательного процесса в двух точках, разделённых дистанцией $\lambda$ [м] в направлении распространения волны, составляет в угловых единицах ровно $2\pi$ радиан, что соответствует полному циклу колебания.

Универсальные соотношения между длиной волны и частотой

Видеоурок: длина волны

Взаимосвязь между длиной волны, фазовой скоростью $v$ и частотой $f$ можно вывести, исходя из фундаментального определения волнового процесса. Длина волны эквивалентна пространственной периодичности волнового явления, то есть дистанции, преодолеваемой точкой с неизменной фазой за временной интервал, равный периоду $T$ колебательного процесса. Следовательно, мы можем сформулировать следующее математическое выражение:

$\lambda =vT={\frac {v}{f}}={\frac {2\pi v}{\omega }}.$

Эта формула демонстрирует универсальный характер и применима к волновым процессам различной природы, включая акустические, электромагнитные и иные типы волн. Она устанавливает прямую пропорциональность между длиной волны и фазовой скоростью, а также обратную пропорциональность между длиной волны и частотой (или угловой частотой) колебаний.

Данное соотношение играет ключевую роль в понимании и анализе волновых явлений, позволяя связать пространственные и временные характеристики волнового процесса в единую математическую модель.

Случай электромагнитной волны

В вакууме

Для электромагнитных волн, распространяющихся в вакууме, скорость $v$ в вышеупомянутой формуле эквивалентна скорости света (299 792 458 м/с). Следовательно, длина такой волны вычисляется по формуле:

$\lambda ={\frac {299\,792\,458~{\text{m/s}}}{f}}$

Где $f$ — частота в герцах, $\lambda$ — длина волны в метрах.

Для приблизительных расчётов длины электромагнитной волны в свободном пространстве можно использовать упрощённый метод: разделить 300 000 км/с на частоту в килогерцах. Погрешность такого расчёта составляет около 0,07%.

В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.

Альтернативный подход заключается в запоминании удобной пары «частота-длина волны», например, 100 МГц соответствует 3 м. Используя это соотношение, можно определить длину волны для других частот. К примеру, 1 МГц (в 100 раз ниже 100 МГц) соответствует длине волны 300 м.

Рассмотрим некоторые характерные частоты и соответствующие им длины волн:

• 50 Гц (промышленная частота электросети) — 6000 км;
• 100 МГц (FM-радиовещание) — 3 м;
• 900 МГц и 1800 МГц (мобильная связь) — 33,3 см и 16,7 см соответственно;
• 2,4 ГГц (Wi-Fi) — 12,5 см;
• 10 ГГц (бортовые РЛС современных истребителей) — 3 см.

Область видимого света охватывает электромагнитное излучение с длинами волн от 380 до 780 нм.

Классификация радиоволн основывается на их длине:

• декаметровые (короткие) волны: 10-100 м;
• метровые волны: 1-10 м;
• дециметровые волны: 0,1-1,0 м.

Длина волны существенно влияет на характеристики распространения радиоволн, включая дифракцию, отражение от объектов, дальность связи и радиолокации.

Размеры антенн обычно сопоставимы с рабочей длиной волны или превышают её, особенно для направленных антенн. Однако антенна средневолнового диапазона, несмотря на значительно меньшие габариты по сравнению с длиной волны, сохраняет способность к пространственной селекции сигналов.

В веществе

При распространении электромагнитной волны в материальной среде её длина определяется формулой:

$\lambda ={\frac {c}{nf}},$

где $n={\sqrt {\varepsilon \mu }}$ — коэффициент преломления вещества, $\varepsilon$ и $\mu$ — относительные диэлектрическая и магнитная проницаемости соответственно. Важно отметить, что $\varepsilon$ и $\mu$ могут значительно варьироваться в зависимости от частоты $f$ (явление дисперсии).

Следовательно, при расчётах необходимо использовать значения $\varepsilon$ и $\mu$, соответствующие рассматриваемой частоте, а не их статические величины.

В большинстве случаев $n>1$ (за исключением крайне высоких частот в рентгеновском диапазоне), что приводит к $n>1$. Как следствие, длина волны в веществе обычно меньше, чем в вакууме при той же частоте.

В радиочастотном диапазоне для многих сред $\mu \approx 1$ (практически равно единице для диэлектриков, стремится к единице с увеличением частоты для ферромагнетиков). Поэтому в инженерной практике часто применяют величину $1/{\sqrt {\varepsilon }}<1$, именуемую коэффициентом укорочения. Она представляет собой отношение длины волны в среде к длине волны в вакууме. Например, для полиэтилена, широко используемого в радиотехнике как изолятор с низкими потерями, $\varepsilon$ = 2,56, что даёт коэффициент укорочения $1/{\sqrt {\varepsilon }}$ ≈ 0,625.

Особый интерес представляют волноводы, где длина электромагнитной волны (как поперечномагнитной, так и поперечноэлектрической) может превышать не только длину волны в среде с аналогичным $\varepsilon$, но даже длину волны в вакууме. Это обусловлено тем, что фазовая скорость электромагнитной волны в волноводе может быть выше, чем скорость распространения волны в среде с тем же значением $\varepsilon$.

Случай акустической (упругой) волны

В области акустики фундаментальная взаимосвязь между длиной волны и частотой сохраняет свою значимость, однако требует уточнения: в данном контексте $v$ интерпретируется как скорость распространения звука в конкретной среде, будь то газообразная (например, воздух) или твёрдая.

Для иллюстрации рассмотрим зависимость длины звуковой волны в воздушной среде от частоты:

$\lambda ={\frac {332+0.6\Theta }{f}}$.

В этой формуле $\Theta$ обозначает температуру по шкале Цельсия, $f$ представляет частоту в герцах, а результирующая длина волны $\lambda$ выражается в метрах. Данное соотношение учитывает влияние температуры на скорость распространения звука в воздухе.

Важно отметить существенное различие между акустическими и электромагнитными волнами: в то время как последние способны распространяться в вакууме, звуковые колебания требуют наличия материальной среды и, следовательно, не могут существовать в безвоздушном пространстве.

Случай квантовомеханической волны де Бройля

В рамках квантовой механики концепция волн де Бройля устанавливает волновые характеристики для материальных частиц. Эта теория связывает корпускулярные и волновые свойства материи, приписывая каждой частице определённую длину волны.

Для частицы, обладающей энергией $E$ и импульсом $p$, волны де Бройля характеризуются следующими параметрами:

• Частота колебаний $(f)$ выражается отношением энергии частицы к постоянной Планка $(h)$: $f={\frac {E}{h}}$,
• Длина волны $(\lambda )$ определяется как отношение постоянной Планка к импульсу частицы: $\lambda ={\frac {h}{p}}$.

Эти соотношения демонстрируют дуалистическую природу материи, объединяя волновые и корпускулярные аспекты в единую квантово–механическую картину мира.

Литература

• Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).

Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!