Архимед

Архимед
Дата рождения	287 год до н. э.(-287)
Место рождения	Сиракузы
Дата смерти	212 год до н. э.(-212)
Место смерти	Сиракузы
Научная сфера	математика, астрономия, механика, инженерия

Архиме́д (287, Сиракузы, Сицилия — 212 год до н. э.) — древнегреческий учёный, математик, механик. Родился и большую часть жизни прожил в городе Сиракузы (Сицилия). Его математические работы намного опередили своё время и были правильно оценены только в эпоху создания дифференциального и интегрального исчисления. Заложил основы механики, гидростатики, автор ряда важных изобретений.

Биография

Архимед родился в 287 году до н. э. в в городе Сиракузы в семье астронома Фидия, который и обучил сына математическим наукам. Это была знатная, но небогатая семья. Архимед находился в родственных связях с Гиероном, который во время Пирровой войны настолько отличился, что после ухода Пирра назад в Грецию ему удалось захватить неограниченную власть в Сиракузах. Это отразилось на материальном положении его ближайших родственников, и молодой Архимед скорее всего смог отправиться в Александрию для дальнейшего обучения. В Александрии он получает образование у последователей Евклида, сближается с рядом математиков, среди которых были Конон, Досифей, Эратосфен, Дзейксипп. По окончании обучения Архимед возвращается в Сиракузы, где занимается научной деятельностью.

Архимед сдвигает Землю

В одном из писем Гиерону Архимед писал, что малой силой можно возможно привести в движение сколь угодно большую тяжесть.

Дай мне, где стать, и я сдвину Землю.Архимед

Гиерон был очень удивлён и попросил показать, как это возможно. Архимед продемонстрировал это над грузовым трёхмачтовым судном. Встав неподалёку на берегу, нажимая рукой на конец полиспаста, он смог придвинуть гружёное судно. Гиерон был поражен и склонил Архимеда к изобретению машин как для обороны, так и для нападения.

Шар, вписанный в цилиндр

В наибольшей степени Архимед проявил себя, как инженер, весной 214 года до н. э. во время осады Сиракуз. Он соорудил машины, которые позволяли отражать атаки. Среди этих машин были те, которые могли метать снаряды на различные расстояния, другие имели железную лапу и запросто могли потопить любой корабль. Часть машин разила короткими стрелами через предварительно приготовленные в городской стене отверстия. Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Осенью 212 года до н. э. Сиракузы были взяты римлянами. Это произошло во время праздника Артемиды, когда охранники были пьяны. Один из охранников открыл врагу потайной ход в стене. Во время штурма города Архимед был убит. Согласно желанию Архимеда, на его могиле был высечен шар, вписанный в цилиндр. По этому признаку спустя полтора столетия могилу учёного разыскал Цицерон.

Научная деятельность

Математика

Кубооктаэдр

Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат исследования по геометрии, арифметике, алгебре. Архимед построил счисление, позволяющее записывать и называть большие числа. Он с большой точностью вычислил значение числа $\pi$ и указал пределы погрешности

3${\tfrac {10}{71}}$<$\pi$<3${\tfrac {1}{7}}$.

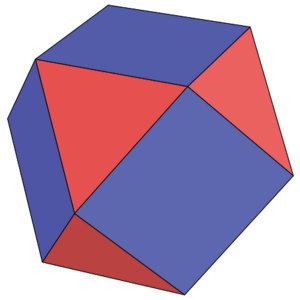
Ему принадлежит открытие 13 типов полуправильных многогранников — «архимедовых тел», полная теория о которых была позднее восстановлена Иоганном Кеплером в 1619 году. Архимед значительно развил учение о конических сечениях.

Архимед представил геометрический способ решения кубических уравнений вида, корни которых он находил с помощью пересечения параболы и гиперболы, провёл полное исследование этих уравнений, нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.

Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. В своей работе «Послание к Эратосфену о методе» (иногда называемой «Метод механических теорем») он использовал бесконечно малые для вычисления объёмов.

В сочинениях «О шаре и цилиндре», «О спиралях», «О коноидах и сфероидах» Архимед применяет метод верхних и нижних интегральных сумм, которые в настоящее время называют суммами Римана или Дарбу. Постулаты, приведённые в начале первой книги сочинения «О шаре и цилиндре», позволили найти поверхность сферы и сферического сегмента и дать метод вычисления длины окружности с любой степенью точности.

В сочинении «Квадратура параболы» Архимед доказал, что площадь сегмента параболы, отсекаемого от неё прямой, составляет 4/3 от площади вписанного в этот сегмент треугольника. В математике, естественных науках и технике очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин — их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объём? Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления. Архимед первым увидел связь этих задач с проблемами определения касательных и показал, как решать задачи на экстремумы.

Физика

Закон рычага

Теория рычага, изложенная в труде Архимеда «О равновесии плоских фигур» долгое время являлась основой механики. В основе этой теории лежат следующие постулаты:

1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине;
2. Если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-нибудь прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой было прибавлено;
3. Точно так же если от одной из тяжестей будет отнято что-нибудь, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято.

На основании этих постулатов Архимед сформулировал закон рычага следующим образом: «Соизмеримые величины уравновешиваются на длинах, которые будут обратно пропорциональны тяжестям. Если величины будут несоизмеримы, то они точно так же уравновесятся на длинах, которые обратно пропорциональны этим величинам».

В том же труде Архимедом дано определение центра тяжести тела как «некоторая расположенная внутри его [тела] точка — такая, что если за неё мысленно подвесить тело, то оно остаётся в покое и сохраняет первоначальное положение». Также им были описаны принципы расчёта центра тяжести треугольника, параллелограмма, трапеции, сегмента параболы, криволинейной трапеции, боковые стороны которой являются дугами парабол.

Изложенные Архимедом принципы работы рычагов и понятие центра тяжести практически в неизменном виде используются и на сегодняшний день. Архимед прославился многими механическими конструкциями. Рычаг был известен и до него, но лишь Архимед изложил его полную теорию и успешно её применял на практике. Плутарх сообщает, что Архимед построил в порту Сиракуз немало блочно-рычажных механизмов для облегчения подъёма и транспортировки тяжёлых грузов. В легенде о том, как Архимед движением руки начал двигать корабль, современники видят работу не рычага, а полиспаста или многоступенчатого редуктора, который сумел создать древнегреческий сиракузский учёный.

Закон Архимеда

Известный закон Архимеда изложен в сочинении «О плавающих телах». Он формулирует основное положение: «Поверхность всякой жидкости, установившейся неподвижно, будет иметь форму шара, центр которого совпадает с центром Земли». Архимед считает Землю шаром и поверхность тяжелой жидкости, находящейся в равновесии в поле тяжести Земли, сферической. Он доказывает, что тела одинакового удельного веса с жидкостью погружаются настолько, что их поверхность совпадает с поверхностью жидкости. Более лёгкое тело погружается настолько, что объём жидкости, соответствующий погружённой части тела, имеет вес, равный весу всего тела. Путем логических рассуждений Архимед приходит к предположениям, содержащим формулировку его закона:

«VI. Тела более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела».

«VII. Тела более тяжёлые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объёме, равном объёму погружённого тела».

В остальных предложениях первой и второй книги Архимед разбирает условия равновесия тел, плавающих в жидкости, причем тела имеют форму сферического или параболического сегмента.

Инженерная деятельность

Механизм для подачи воды

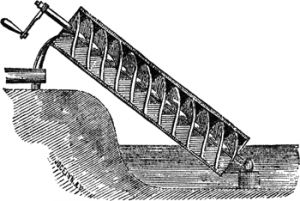
Как инженер, Архимед проявил себя именно при осаде Сиракуз, хотя изобретать начал еще задолго до этого времени. Метательные машины были известны очень давно, но учёному с помощью соответствующих расчётов удалось добиться различной дальнобойности. К оборонительным машинам ближнего действия относят изобретения, получившие названия «железные лапы» или «сбрасыватели камней». Архимед занимался строительным делом. Так, при построении бойниц, он решил задачу об определении давлений на колонны, подпирающих длинную балку или стену. Большую известность получил Винт Архимеда («улитка») — механизм, использующийся для подачи воды из низколежащих водоёмов на поверхность.

Астрономия

На сегодняшний день мы располагаем информацией о трёх работах учёного по астрономии. В сочинении «Псаммит» Архимед задался вопросом о размере Вселенной. Ипполит Римский (170—230-е годы н. э.) в приписываемом ему трактате «Обличение всех ересей» приводит расстояния между планетами, взятые из утерянных в настоящее время работ Архимеда.

В «Псаммите» он экспериментальным путём нашёл угловой диаметр Солнца — от 27’ до 32’55". Истинное значение показателя составляет 31’28"—32’37". Как подчёркивают современные авторы, Архимеду удалось впервые определить данную величину.

Архимед построил планетарий или «небесную сферу», в котором можно было наблюдать фазы Луны, движение планет, затмение Солнца и Луны. Занимался проблемой определения расстояний до планет. Предположительно в основе его вычислений лежала система мира с центром в Земле, но планетами Меркурием, Венерой и Марсом, обращающимися вокруг Солнца и вместе с ним — вокруг Земли. В своём сочинении «Псаммит» он донёс информацию о гелиоцентрической системе мира Аристарха Самосского.

Сведения о некоем «небесном глобусе», который наглядно изображал систему мира с Землёй в центре, вокруг которой вращаются Солнце, Луна и планеты, содержатся в нескольких античных источниках. Цицерон, в пересказе, передаёт слова Гая Сульпиция Галла, который якобы видел в доме Марцелла устройство, сконструированное Архимедом, и привезённое завоевателем Сиракуз в качестве трофея. Одновременно он говорит о более известной «другой сфере Архимеда», которую Марцелл передал в храм Доблести. Это устройство упоминали Овидий, Лактанций и Клавдий Клавдиан.

Сочинения

1. «Квадратура параболы» — здесь обосновывается, что площадь сегмента параболы равна 4/3 вписанного в неё треугольника. Это первое из нескольких посланий Досифею, написанное вскоре после смерти Конона (около 220 года до н. э.). Это две самостоятельные работы, посвящённые решению одной задачи — нахождению площади параболического сегмента, отсечённого прямой, перпендикулярной к оси параболы. В первой работе задача решается механическим методом (собственное изобретение Архимеда), во второй — геометрическое решение методом Евдокса.
2. «Книга опор» — недошедшее до нас сочинение. Его отрывки сохранились в «Механике» Герона.
3. «О шаре и цилиндре» — трактат из двух частей (др.-греч. περὶ σφαίρας καὶ κυλίνδρου). В нём Архимед доказал, что площадь любой сферы радиуса r в четыре раза превышает площадь её наибольшего круга (в современных обозначениях S=4$\pi$r²); объём шара равен 2/3 того цилиндра, в который он вписан, и это с учётом объёма цилиндра приводит к получению формулы объёма шара $\pi$r³. Там же приводится аксиома Архимеда.
4. «Измерение круга» (др.-греч. κύκλου μέτρησις) в дошедшем до нас виде представляет сочинение из трёх теорем. Первая даёт описание определения площади круга как произведения полупериметра на радиус. Третья выводит отношение между длиной окружности и диаметром, известное как число $\pi$ . Вторая, которую следовало бы поместить после третьей, приводит классический метод вычисления площади круга;
5. «О коноидах и сфероидах» (др.-греч. περὶ κωνοειδέων καὶ σφαιροειδέων) — первое произведение среди всей мировой математической литературы, в котором рассматриваются поверхности второго порядка. Основной задачей, решение которой Архимед приводит в сочинении, является определение объёмов сегментов параболоида, гиперболоида и эллипсоида вращения;
6. Трактат «О спиралях» (др.-греч. περὶ ἑλίκων) написан позже двухтомника «О шаре и цилиндре» и до сочинения «О коноидах и сфероидах». Тема трактата была предложена Архимеду Кононом. Сиракузский учёный описывает множество свойств спирали, которая представляет линию, соединяющую местоположения точки, движущейся с одинаковой скоростью вдоль прямой линии, которая сама вращается с постоянной скоростью вокруг фиксированной точки. Полученную кривую называют Архимедовой спиралью;
7. Трактат «О равновесии плоских фигур» (др.-греч. περὶ ἰσορροπιῶν) состоит из двух книг, в которых выводится закон равновесия рычага; доказывается, что центр тяжести плоского треугольника находится в точке пересечения его медиан; содержатся определения центров тяжести треугольника, параллелограмма, трапеции, параболического сегмента, трапеции, боковые стороны которой являются дугами парабол. Понятие центра тяжести предполагается известным, и в начале книги приводятся постулаты о центрах тяжести.
8. «Псаммит» (в дословном переводе «О счислении песчинок»). Одно из последних сочинений Архимеда.
9. «О плавающих телах» (др.-греч. περὶ τῶν ὀχουμένων) относится к числу поздних сочинений Архимеда, возможно, представляя собой последнее из них. В этом сочинении изложен знаменитый закон Архимеда.
10. «Стомахион» (др.-греч. στομάχιον) был обнаружен в начале XX века в палимпсесте и посвящён древнегреческой головоломке, состоящей в составлении квадрата из многоугольников, на которые он был вначале разрезан. Задача состоит в сборке квадрата из 14 его частей, среди которых 1 пятиугольник, 2 четырёхугольника и 11 треугольников;
11. «Послание к Эратосфену о механическом методе» (др.-греч. πρὸς Ἐρατοσθένην ἔφοδος), или «Эфод», также обнаружен в начале XX века. Он описывает процесс открытий в математике. Это единственное античное произведение, затрагивающее данную тему.
12. Трактат «Задача о быках» (др.-греч. πρόβλημα βοεικόν) Архимед ставит задачу, приводимую к уравнению Пелля. Эта работа была обнаружена Готхольдом Эфраимом Лессингом в греческой рукописи, состоящей из стихотворения в 44 строки. Текст задачи был опубликован в издании «Beiträge zur Geschichte und Litteratur» в Брауншвейге в 1773 году. Авторство Архимеда не вызывает сомнений, так как и по стилю, и по характеру трактат соответствует математическим эпиграммам той эпохи. «Задача о быках» упоминается в одном из античных схолиев к диалогу Платона «Хармид, или о благоразумии». Она адресована Эратосфену и математикам Александрии. Архимед ставит им задачу подсчитать количество голов скота в стаде Гелиоса. Полное решение задачи было впервые опубликовано только в 1880 году;
13. Трактаты «О касающихся кругах» и «О началах геометрии» сохранились в рукописи арабского математика Сабит ибн Курра (836—901), хранящейся в библиотеке города Патна в Индии. Их издали в 1940 году в Хайдарабаде;
14. «Книга лемм» сохранилась в виде арабской обработки и её латинского перевода. Историю книги можно представить так. Арабский математик Сабит ибн Курра перевёл ряд принадлежащих Архимеду текстов. Затем через столетие персидский математик из Багдада Абу Сахль аль-Кухи систематизировал перевод предшественника. Ещё через полвека третий учёный Ан-Насави написал комментарии, а затем четвёртый, чьё имя достоверно не известно, сократил получившийся текст. Латинский перевод арабского текста, отстоящего от Архимеда четырьмя переработками, был опубликован в 1659 году. В книге приведены сведения о проблеме трисекции угла, а также способ определения площади салинона;
15. «Книга о построении круга, разделённого на семь равных частей» состоит из трёх трактатов: «О свойствах прямоугольных треугольников», «О кругах» и «О построении правильного семиугольника». Они также сохранились до наших дней благодаря арабской рукописи;
16. «О касающихся кругах»;
17. «Нахождение высоты и площади треугольника по его сторонам» сохранился благодаря переводу средневекового персидского учёного Аль-Бируни;
18. «Трактат о построении около шара телесной фигуры с четырнадцатью основаниями»;
19. «Часы Архимеда»;
20. Трактат «О параллельных линиях» в переработке Сабита ибн Курры «Книга о том, что две линии, проведённые под углами, меньшими двух прямых, встречаются», как указывают рецензенты, не приведён в указанном собрании сочинений. По их мнению, включение этого трактата в сборник наследия Архимеда оправдано так же, как и приведённые трактаты, дошедшие до наших дней исключительно в переводе и обработке средневековых арабских учёных.
21. «Катоптрика» — оптическое сочинение, не дошедшее до нас. Архимед доказывал, что в зеркале угол падения равен углу отражения.

Память

С именем Архимеда связаны многие математические понятия. Например, архимедовы число, граф, аксиома, закон, тело и другие.

В 2004 году во Флоренции был открыт музей математики «Сад Архимеда».

Именем Архимеда назвали один из первых винтовых пароходов «Архимед», заложенный в 1838 году и спущенный в 1839 году в Великобритании. Также в 1848 году на воду спустили первый русский винтовой пароход «Архимед». Его судьба оказалась печальной. Осенью 1850 года он разбился у датского острова

Один из рассказов сборника «Книга апокрифов» классика чешской литературы Карела Чапека носит название «Смерть Архимеда». Автор утверждает, что дело обстояло совершенно не так, как утверждалось ранее. Согласно повествованию Чапека, в дом к Архимеду приходит центурион Люций. Между ним и Архимедом происходит диалог, в ходе которого римлянин пытается убедить учёного перейти на сторону Рима. Во время разговора с Люцием Архимед произносит «Осторожно, не сотри моих кругов». Рассказ заканчивается: «Несколько позже было официально объявлено, что известный учёный Архимед погиб в результате несчастного случая».

Кино:

• 1914 — Кабирия (Cabiria) — худ. фильм, режиссёр — Джованни Пастроне, Архимеда играет Энрико Джемелли;
• 1960 — «Осада Сиракуз»(L’assedio di Siracusa) — итальянский художественный фильм режиссёра Пьетро Франчиши, Архимеда играет Россано Брацци;
• 1972 — «Коля, Оля и Архимед», режиссёр — Юрий Александрович Прытков. Мультфильм СССР.
• 2023 — «Индиана Джонс и Колесо судьбы», режиссёр — Джеймс Мэнголд, Архимеда играет Насер Мемарзиа.

В астрономии в честь Архимеда названы: кратер Архимеда (29,7° N, 4,0° W) и горная цепь Montes Archimedes (25,3° N, 4,6° W) на Луне; астероид (3600) Архимед, открыт 26 сентября 1978 года Людмилой Васильевной Журавлёвой в Крымской астрофизической обсерватории, название присвоено 4 июня 1993 года.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!