Судоку

Судоку

Судо́ку (яп. 数独 су:доку, произношение ) — это головоломка с цифрами. Судоку представляет собой латинский квадрат 9-го уровня. Иногда его ошибочно называют магическим квадратом. Пазлы судоку часто печатаются в газетах и журналах по всему миру, и множество сборников судоку выходит в свет крупными тиражами. Решение судоку широко распространено как популярное развлечение.

Правила

Игровая доска представляет собой квадрат размером 9×9, разделённый на более мелкие квадраты со стороной в 3 клетки — всего 81 клетка. В них заранее размещены некоторые цифры (от 1 до 9), известные как подсказки. Задача игрока — заполнить пустые клетки числами от 1 до 9 так, чтобы в каждой строке, каждом столбце и каждом из девяти малых квадратов 3×3 каждая цифра появлялась только однажды.

Сложность судоку варьируется в зависимости от количества начальных подсказок и используемых стратегии для решения. Простейшие судоку решаются методом исключения: всегда есть хотя бы одна ячейка, куда подходит только одно значение. Некоторые пазлы решаются за считанные минуты, другие могут занять несколько часов.

Грамотно составленная головоломка имеет единственное правильное решение. Тем не менее, на некоторых веб-сайтах могут встречаться судоку с несколькими решениями или с путанными шагами, под видом более сложных задачек.

Происхождение

В XVIII веке Леонард Эйлер создал игру под названием «Carré latin» («Латинский квадрат»). Именно на базе этой игры в 1970-х годах в Северной Америке были разработаны определённые числовые головоломки. Так, судоку впервые появилась в США в 1979 году на страницах журнала «Dell Puzzle Magazine» под названием «Number Place». По-настоящему популярной судоку стала в 1980-х и 1990-х годах, когда японская издательская компания «Nikoli» начала регулярно включать её в свои выпуски (с 1986 года). Сегодня судоку — это неотъемлемая часть многих газет, в том числе изданий с многомиллионной аудиторией, таких как немецкая «Die Zeit» и австрийская «Der Standard». В России судоку также активно публикуются в различных газетах, журналах и специальных сборниках.

Математическая основа

Задача обобщённого судоку на сетке размеров $N^{2}\times N^{2}$ относится к NP-трудным, ввиду того что заполнение латинского квадрата является подзадачей этой головоломки.

Совокупное количество возможных уникальных решений судоку стандартного размера 9×9 составляет

6 670 903 752 021 073 000 000 (Шаблон:OEIS),

что математически можно представить в виде $6{,}67\times 10^{21}$. Однако, если считать идентичными те решётки судоку, которые можно получить путём симметрий, поворотов и перенумераций, общее количество таких уникальных решений снижаетcя до 5 472 730 538 (Шаблон:OEIS).

Вопрос о минимальном числе подсказок, требующихся для однозначного решения судоку, долго не имел однозначного ответа. В частности, неизученным оставался вопрос о существовании уникально решаемого судоку с 16 подсказками. Для выяснения этого на платформе BOINC при проекте распределённых вычислений Sudoku@vtaiwan велись поиски таких решёток. В январе 2012 года были подтверждены данные, что уникально решаемые судоку с только 16 подсказками отсутствуют.

Методы поиска решения

Начинается всё с анализа рядов, колонок и 3×3 блоков с наибольшим количеством заполненных клеток: проще решать те участки, где остался минимальный выбор. При заполнении клетки следует внимательно проверять её колонку, ряд и блок 3×3, чтобы исключить повторение всех остальных восьми чисел. Если в блоке 3×3 осталось несколько пустых ячеек и только одна из них подходит для конкретного числа, это число вписывают в данную ячейку. Перед заполнением важно убедиться, что вводимое число не появляется в той же колонке, строке или блоке 3×3.

Когда в одном столбце, строке или блоке 3×3 в трех различных ячейках возможны кандидаты {1,2; 1,2; 1,3}, значит третья ячейка должна содержать число 3. Ведь если бы это было число 1, то одна из первых двух ячеек должна бы содержать число 2, а другая осталась бы пустой, что противоречит правилам, согласно которым все клетки должны быть заполнены.

Для ускорения решения головоломки существуют две стратегии.

Первая стратегия заключается в нахождении числа, которое присутствует в большинстве строк, колонок или блоков 3×3. В каждом блоке 3×3, где это число отсутствует, ищутся другие блоки 3×3 в тех же ряду и колонке, где это число присутствует. Исключаются те места в решаемом блоке, куда данное число не может быть вписано, что позволяет легко найти единственную подходящую ячейку.

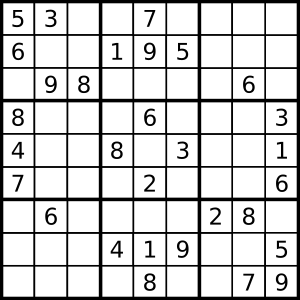
Пример:

Цифра 9 присутствует в шести различных блоках 3×3. Следовательно, её можно безопасно разместить в центральном нижнем блоке 3×3 в верхнем левом углу, а также в центральном правом блоке 3×3 в первой ячейке первого ряда. Что касается центрального блока 3×3, то здесь цифра 9 может находиться исключительно в третьей ячейке второго ряда.

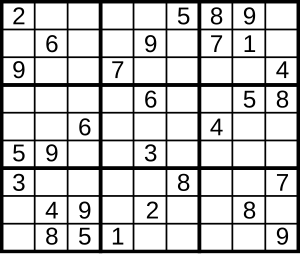
Пример:

Центральные ряды верхнего и нижнего квадратов 3x3 почти полностью заняты. В верхнем центральном блоке три пропущенные цифры: 1, 4 и 9. При тщательном анализе становится ясно, что цифра 4 занимает центральное место блока, 1 находится в правом верхнем углу, а 9 располагается в левом верхнем углу. Точно так же следует поступить и с нижним центральным блоком 3x3, где недостающими являются цифры 6, 8 и 9. Сперва ставим 6 в центр блока, затем 9 в правый нижний угол, а 8 в левый нижний угол.

Для решения наиболее сложных судоку используется исключающий метод («нить Ариадны»). Берётся лист в клетку и фиксируется текущее состояние головоломки, затем отмечается клетка с двумя возможными цифрами, которые, при подстановке, позволят определить как можно большее количество пар в других клетках. Выбирается одна из цифр и подставляется в черновик. В половине случаев решение окажется неверным, указывая, что выбранная цифра была неправильной. Нужно «смотать нить» — вернуться к исходной клетке и попробовать другой вариант. При отсутствии ошибок правильным будет второе число. Эту технику описал Моулер Клив, разработчик пакета для научных расчётов MATLAB.

Разновидности

Существует множество вариаций судоку:

• Нерегулярное судоку (иногда называемые Судоку-пазлы, Судоку-фигуры или Области). В этих головоломках используются произвольные формы областей вместо традиционных блоков 3x3. Основное правило сохраняется: цифры не должны повторяться в рамках каждой области.
• Судоку разных размеров. Такие головоломки могут существенно варьироваться по размеру, начиная от небольших 4x4 (эти уменьшенные версии известны как «шидоку» (Shidoku), где shi — с японского четыре), и доходя до больших 25x25. Чаще всего встречаются небольшие версии для детей.
• Судоку с дополнительными областями. В этих задачах к стандартным областям (вертикалям, горизонталям и блокам) добавляются новые зоны, где также запрещено повторение цифр. Обычно это диагональные судоку.
• Судоку с дополнительными условиями. В таких вариантах, помимо стандартных ограничений, добавляются новые правила:
  • Судоку «Суммы» и другие его вариации (например, «Судоку-Произведения», «Судоку-Арифметика», «Квадросудоку», «Суммы-сбоку», «Диагональные суммы» и др.), где на поле указывается сумма (или произведение, разность и т.д.) всех цифр внутри блока.
  • Судоку «Чёт-нечёт». В этих головоломках некоторые клетки выделены цветом, обозначая, что в них должны находиться только чётные или только нечётные цифры.
  • Судоку «Больше-меньше». В этих задачах между некоторыми соседними клетками указывается знак сравнения, показывающий, в какой из клеток цифра больше.
  • Судоку «Точки». Между соседними клетками может быть поставлена белая или чёрная точка, если соседние цифры различаются на 1 или кратны двум.
  • Судоку «Перегородки» (или «Судоку-Соседи»). В этих версиях помечены все пары соседних клеток, где цифры отличаются на 1.
  • «Шахматные» судоку, где некоторые клетки связаны правилами хода шахматных фигур (чаще коня), и такие клетки не могут содержать одинаковые цифры. Это ограничение может распространяться на все или некоторые цифры.
  • Судоку различной формы. Здесь вместо стандартной квадратной структуры используются треугольные, шестиугольные и более сложные формы сетки.
• Соединённые судоку. «Судоку-Самурай» (также известное как «Судоку-Комбо», «Судоку-Конструкции», «Тудоку» и пр.), где несколько отдельных головоломок имеют общие области и решаются взаимосвязано.

Настольная игра судоку

Существует также настольная версия этой головоломки. Множество компаний по всему миру выпустили свои собственные настольные варианты судоку (например, популярный дизайнер настольных игр Reiner Knizia представил свою адаптацию этой логической игры). В России можно найти настольное судоку от компании Астрель и польской компании Trefi.

Компьютерные игры

Для персональных компьютеров разработаны многочисленные версии этой игры, такие как:

• Sudoku (в составе игрового пакета GNOME Games) или KSudoku (в составе игрового пакета KDE Games) — для платформ на основе Linux;
• Microsoft Sudoku (распространяемый через Windows Store и совместимый с операционными системами Windows 8.1 и Windows 10) — для платформ на базе Windows.

Версии для мобильных телефонов

Для мобильных устройств и смартфонов созданы многочисленные вариации этой игры. Эти версии удобны тем, что они могут автоматически создавать условия головоломки. Они также могут указывать на ошибки (подсвечивая противоречивые цифры) или предоставлять подсказки для их решения. 9 цифр в традиционной судоку, назначенные на 9 цифровых кнопок на мобильном устройстве, делают процесс игры чрезвычайно удобным.

С появлением смартфонов игра завоевала заслуженное место среди самых популярных. С появлением на рынке устройств, основанных на Android и iOS, число поклонников игры значительно увеличилось.

• Puzzazz Crossword & Puzzle: приложение-головоломка для iPhone и iPad.
• Genina.com: приложение для судоку для Android и iOS.
• Andoku Sudoku 3:приложение для судоку для Android:

См. также

• Латинский квадрат
• Четыре четвёрки

Ссылки

• Правила игры судоку и её разновидностей.
• Техника X-крыла Судоку.
• Техника Меч-рыба

Литература

• Эндрю Херон, Эдмунд Джеймс. Судоку для «чайников» = Su Doku for Dummies (Sudoku). — М.: «Диалектика», 2007. — С. 336. — ISBN 978-0-470-01892-7.
• Кноп К. Магический квадрат или Числа на плацу // Компьютерра. — Вып. 09.09.2000.
• Сухин И. Г. Судоку и суперсудоку на шестнадцати клетках для детей. — М.: АСТ, Астрель, 2006. — 128 с. — ISBN 5-17-036566-7.

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!