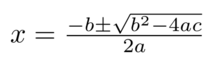Рациональные уравнения

Материал из «Знание.Вики»

Рациона́льные уравне́ния — это уравнения, содержащие в себе рациональные выражения, включая переменные. Обычно рациональные уравнения представлены или в виде дроби, где числитель и знаменатель представлены многочленами или целые, когда все переменные находятся в числителях[1].

История

Диофант Александрийский

Некоторые алгебраические приёмы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Это было обусловлено потребностью решать практические задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера[2].

Немало свойств, правил, алгебраических приёмов знали учёные Древней Греции. Они выражали их в геометрической форме. Например, Евклид около 300 год до н. э. занимался вопросами превращения одних фигур в другие, им равные. В «Началах» решается задача о построении квадрата, равного любому данному многоугольнику. При этом Евклид прибегает к использованию самих площадей, а не чисел, которые выражают эти площади. То, что люди получают с помощью алгебры, Евклид получал геометрическим путем. Извлечение квадратного корня из числа говорило для Евклида о построении стороны квадрата, площадь которого равна площади данного многоугольника. Со следами геометрической алгебры мы сталкиваемся и по сей день в терминах «квадрат» числа, «куб» числа.

Процесс избавления алгебры от геометрической формы и возникновение буквенной символики начался в III веке до н. э. в Древней Греции, в трудах Диофанта, и продлился в Индии и в средние века в арабских странах и в Европе. Только после того, как Виет, живший в годы между 1540 и 1603, ввёл буквенные обозначения для неизвестных и известных величин, а также коэффициентов, после того как появились труды Декарта, жившего с 1596 по 1650 год, Ньютона и другие учёные, этот долгий исторический этап был в основном завершён. Благодаря введению буквенных коэффициентов стало возможным изучение алгебраических уравнений в общем виде и использование общих формул[3].

Виды рациональных уравнений

Целое (алгебраическое) рациональное уравнение

Это уравнение, в котором есть только сложение, вычитание, умножение, деление и возведение в целую степень[4].

Это уравнение принимает вид: Pn(x) = a0 xn + a1xn-1 + … + an-1x + an , a0 ≠ 0[5].

Дробно-рациональное уравнение

Это рациональное уравнение, в котором левая или правая части являются дробными выражениями[6]. При решении дробно — рациональных уравнений нужно быть внимательным при сокращении дробей, так как в этом случае можно получить посторонние корни[5].

Виды целых рациональных уравнений

Линейные уравнения

Уравнение обычно записывается в виде aх + b = 0, a ≠ 0 и имеет один корень x = -b/a[7].

Квадратные уравнения

Уравнение записывается в виде ax2 + bx + c = 0 и называется дискриминант квадратного уравнения[5].

Где коэффициенты a, b, c — любые действительные числа, причем a ≠ 0 . Коэффициенты a, b, c различают по названиям: а — первый, или старший, коэффициент; b — второй коэффициент, или коэффициент при х; с — свободный член[5].

Решение такого уравнения можно получить с помощью формулы[8]:

Решение квадратного уравнения

Обычно выражение b2 - 4ac обозначают буквой D (дискриминант)[5].

Если D < 0, то квадратное уравнение не имеет корней.

Если D = 0, то квадратное уравнение имеет один корень, который находится о формуле x = -b/2a.

Если D > 0, то квадратное уравнение имеет два корня, которые находятся по формулам: x1 = (-b + √D)/2a , x2 = (-b - √D)/2a[5].

Неполное квадратное уравнение — это уравнение, в котором присутствуют не все три слагаемых. Это уравнение, у которого хотя бы один из коэффициентов b, c равен нулю.

Решение неполных квадратных уравнений:

1. Если уравнение имеет вид ax2 = 0 , то оно имеет один корень: x = 0.

2. Если уравнение имеет вид ax2 + bx = 0 (b ≠ 0), то используется метод разложения на множители: x(ax + b) = 0; значит, либо x = 0 , либо ax + b = 0.

В итоге получаем два корня: x1 = 0, x2 = -b/a.

3. Если уравнение имеет вид ax2 + c = 0, то его преобразуют к виду ax2 = -c и далее x2 = -c/a.

В случае, если -c/a < 0, уравнение x2 = -c/a не имеет действительных корней (значит, не имеет корней и исходное уравнение ax2 + c = 0).

В случае, когда -c/a > 0, уравнение x2 = -c/a (а значит, и уравнение ax2 + c = 0) имеет два корня: x1,2 = ±√-c/a[5].

Кубические уравнения

Это уравнение третьей степени ax3 + bx2 + cx + d = 0[9].

Биквадратные уравнения

Это уравнение вида ax4 + bx2 + c = 0. Такие уравнения решаются путём замены x2 на y, применив её, получается уравнение вида ay2 + by + c = 0, а после этого полученное значение новой переменной используют для вычисления исходной переменной[1].

Возвратные уравнения

Это уравнение вида ax4 + bx3 + cx2 + bx + a = 0. Такое название они имеют из-за повторения коэффициентов при старших степенях и младших. Для решения такого уравнения сначала делят его на x2:

  • ax4 + bx3 + cx2 + bx + a = 0| ÷x2
  • ax2 + bx + c + b/x + a/x2 = 0
  • a(x2 + 1/x2) + b(x + 1/x) + c = 0

Затем заменяют (x + 1/x) на новую переменную, тогда (x2 + 1/x2) = y2 — 2, после подстановки получается квадратное уравнение:

a(y2 — 2) + by + c = 0. После этого находят корни уравнений x + 1/x = y1 и x + 1/x = y2.

Аналогичным методом решаются возвратные уравнения вида:

ax4 + bx3 + cx2 + kbx + k2a = 0

Корни уравнения вида ax4 + b = 0 находятся с помощью применения формул сокращённого умножения[1].

Другие алгебраические уравнения

Нильс Хенрик Абель

Формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находить корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Нильс Абель в 1824 году, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удаётся легко решить, факторизуя их левую часть, то есть разлагая её на множители. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Уильямом Горнером, Исааком Ньютоном и Карлом Греффе. Во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней[10].

Методы решения

Для целых рациональных уравнений.

Если в задаче речь идёт о таком типе выражений, то следует воспользоваться стандартным алгоритмом действий:

  1. Перенести каждое слагаемое справа налево, чтобы уравнение осталось равным нулю.
  2. Применить алгебраические преобразования, чтобы привести уравнение к виду линейного, квадратного, кубического или другого подходящего формата. Этот процесс может включать раскрытие скобок, сокращение подобных членов, перенос слагаемых на одну сторону уравнения и так далее.
  3. После приведения уравнения к подходящему формату, найти неизвестное. В случае линейного уравнения это может быть простое выражение, а для квадратного — применение формулы квадратного корня или метода дискриминанта.
  4. Проверить полученное решение подстановкой в исходное уравнение[11].

Для дробно — рациональных уравнений.

  1. Приведение к общему знаменателю: Умножить все части уравнения на общий знаменатель, чтобы избавиться от дробей. Затем сократить все одинаковые члены и решить получившееся уравнение[12].
  2. Факторизация: Если это возможно, то факторизовать числитель и знаменатель дроби. Затем сократить подобные члены и решить уравнение.
  3. Замена переменной: В некоторых случаях можно ввести новую переменную, чтобы привести уравнение к более простому виду[1].
  4. Метод исключения: Если есть система дробно-рациональных уравнений, исключить одну переменную из каждого уравнения и решить получившуюся систему линейных уравнений[13].

Примечания

  1. ↑ 1,0 1,1 1,2 1,3 Беляев Е. Н. Решение рациональных уравнений. Справочник от автор 24 (5 марта 2023). Дата обращения: 3 ноября 2023.
  2. ↑ Кокурина Ю. К. Курс лекций по истории математики. — Владимир, 2014.
  3. ↑ Бронникова Л. М. История математики. — Барнаул: ФГБОУ АлтГПУ, 2016. — ISBN 978-5-88210-810-5.
  4. ↑ Целые рациональные уравнения. Дата обращения: 19 ноября 2023.
  5. ↑ 5,0 5,1 5,2 5,3 5,4 5,5 5,6 Фирер А. В., Яковлева Е. Н., Елисова А. П., Захарова Т. В. [https://lpi.sfu-kras.ru/files/elementarnaya_matematika._racionalnye_uravneniya_i_neravenstva_2019.pdf Элементарная математика. Рациональные уравнения и неравенства] / Игнатьева Н. К.. — Красноярск-Лесосибирск: ЛПИ-филиал СФУ, 2019. — 146 с. — ISBN 978-5-7638-4173-2.
  6. ↑ Дробно рациональные уравнения. Дата обращения: 19 ноября 2023.
  7. ↑ Линейные уравнения. Энциклопедия Кругосвет. Дата обращения: 5 ноября 2023.
  8. ↑ Квадратные уравнения. Энциклопедия Кругосвет. Дата обращения: 5 ноября 2023.
  9. ↑ Кубическое уравнение. Справочник от автор 24. Дата обращения: 6 ноября 2023.
  10. ↑ Другие алгебраические уравнения. Энциклопедия Кругосвет. Дата обращения: 5 ноября 2023.
  11. ↑ Беляев Е.Н. Алгоритм решения целых рациональных уравнений. Справочник от автор 24 (05.03.2023). Дата обращения: 3 ноября 2023.
  12. ↑ Восковская Н. И. Решение уравнений с переменной в знаменателе дроби (12 мая 2023). Дата обращения: 19 ноября 2023.
  13. ↑ Семёнов А. В., Юрченко Е. В. Система подготовки к ЕГЭ по математике. — Москва, 2009. — 80 с.
WLW Checked Off icon.svg Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!
Источник — https://znanierussia.ru/articles/index.php?title=Рациональные_уравнения&oldid=130819