Небесная механика

Наука
Небесная механика
англ. Celestial Mechanics
Предмет изучения	движения небесных тел Солнечной системы в гравитационном поле
Период зарождения	XX век
Основные направления	Астрономия
Медиафайлы на Викискладе

Небесная механика — раздел астрономии, в котором изучаются движения небесных тел Солнечной системы в гравитационном поле. Термин введён П.-С. Лапласом в 1799 году. В 1798 году введено понятие «теоретическая астрономия». В англоязычной литературе распространён термин «динамическая астрономия». Все термины считаются синонимами.

Исторический очерк

Пьер Лаплас

Термин Небесная механика впервые был введён Пьером Лапласом в 1798 году, к этому разделу науки он относил теории равновесия и движения твёрдых и жидких тел, составляющих Солнечную систему (и ей подобные), под действием сил тяготения. В русской научной литературе раздел астрономии, посвященный этим проблемам, в течение долгого времени называлась теоретической астрономией. В английской литературе применяется также термин динамическая астрономия.

Страница «Начал» Ньютона с аксиомами механики

Небесная механика принадлежит к числу древнейших наук. Уже в VI веке до нашей эры народы Древнего Востока обладали глубокими астрономическими знаниями, связанными с движением небесных тел. Но в течение многих веков это была только эмпирическая кинематика Солнечной системы. Основы современной Небесной механики были заложены Исааком Ньютоном в «Математических началах натуральной философии» 1687 года. Закон тяготения Ньютона далеко не сразу получил всеобщее признание. Однако уже к середине XVIII века выяснилось, что он хорошо объясняет наиболее характерные особенности движения тел Солнечной системы. В работах Жозефа Лагранжа и Пьера Лапласа были разработаны классические методы теории возмущений. Первая современная теория движения больших планет была построена Урбена Леверье в середине XIX века. Эта теория лежит до сих пор в основе французского национального астрономического ежегодника. В работах Леверье было впервые указано на необъяснимое законом Ньютона вековое смещение перигелия Меркурия, которое оказалось важнейшим наблюдательным подтверждением общей теории относительности. Дальнейшее развитие теория больших планет получила в конце XIX века в работах американских астрономов Саймона Ньюкома и Джордж Уильям Хилл. Работы Ньюкома открыли новый этап в развитии Небесной механики. Чтобы согласовать теорию с наблюдаемым движением Меркурия, Ньюком решил прибегнуть к гипотезе Асафа Холла, который для объяснения невязок в движении больших планет предложил изменить показатель степени в законе тяготения Ньютона.

Первые теории движения Луны были разработаны Алекси Клеро, Жаном Д’Аламбером, Леонардом Эйлером и Пьером Лапласом. Наиболее совершенной с практической точки зрения была теория немецкого астронома Петера Ганзена в 1857 году, которая использовалась в астрономических ежегодниках с 1862 по 1922 годы. В 1867 была опубликована аналитическая теория движения Луны, разработанная французским астрономом Шарля Делоне. Современная теория Луны основана на работах Джорджа Уильяма Хилла в 1886 году. Построение таблиц Луны на основе метода Хилла было начато в 1888 году американским астрономом Эрлом Брауном. Теория движения четырёх спутников Юпитера была разработана ещё Лапласом. В теории, предложенной Виллемом Ситтером в 1919 году и используемой в астрономических ежегодниках, учитываются сжатие Юпитера, солнечные возмущения и взаимные возмущения спутников. Теория движения спутников Сатурна, основанная на классических методах, была построена немецким астрономом Германом Струве. Устойчивость спутниковых систем рассмотрена в работах японского астронома Юсукэ Хагихара в 1952 году.

Наряду с разработкой теории высокой степени точности, но пригодной только на сравнительно небольших интервалах времени (сотни лет), в Небесной механике ведутся также исследования движения тел Солнечной системы в космогонических масштабах времени. Попытки решить эту проблему долгое время не давали удовлетворительных результатов. Только появление быстродействующих вычислительных машин, произведших революцию в Небесной механике, позволило снова вернуться к решению этой фундаментальной задачи. В Советском Союзе и за рубежом разработаны эффективные методы построения аналитической теории движения больших планет, открывающие возможность изучения движения планет на весьма длительных промежутках времени. В связи с разработкой космогонической гипотезы Отто Шмидта в 1940-х годах в Советском Союзе были выполнены многочисленные исследования финальных движений в задаче трёх тел; полученные в этих работах результаты имеют значение на неограниченном интервале времени. В 1965 году в США численным методом была изучена эволюция орбит пяти внешних планет на интервале времени в сто двадцать тысяч лет. Самым интересным результатом этой работы явилось открытие либрации Плутона относительно Нептуна, благодаря которой минимальное расстояние между этими планетами не может быть меньше восемнадцати астрономических единиц, хотя в проекции на плоскость эклиптики орбиты Плутона и Нептуна пересекаются. В 1967 году в СССР выполнена обширная работа по применению теории вековых возмущений к изучению эволюции орбиты Земли на протяжении миллионов лет. Эта работа имеет важное значение для понимания изменения климата Земли в различные геологические эпохи.

Начало XX века отмечено значительным прогрессом в разработке математических методов Небесной механики. Прогресс связан с работами французского математика Анри Пуанкаре, русского математика Александра Ляпунова и финского астронома Карла Зундмана. Последнему удалось решить общую задачу трёх тел с помощью бесконечных степенных сходящихся рядов. Однако ряды Зундмана оказались совершенно непригодными для практического использования из-за их крайне медленной сходимости. Сходимость рядов в Небесной механике тесно связана с проблемой малых делителей. Математические трудности этой проблемы в значительной степени преодолены в работах математиков школы Андрея Колмогорова. Развитие Небесной механики в Советском Союзе тесно связано с деятельностью двух научных центров: Институт теоретической астрономии и кафедры небесной механики Московского университета. В этих двух центрах сложились ленинградская и московская школы, которые определили развитие Небесной механики в нашей стране.

Релятивистская небесная механика

В середине XX века в связи с повышением точности оптических наблюдений небесных тел, развитием новых методов наблюдений и возможностью проведения экспериментов в Небесной механике при помощи космических зондов и искусственных спутников Земли всё большее значение приобретает учёт релятивистских эффектов в движении тел Солнечной системы. Эти проблемы решаются релятивистской небесной механикой, опирающейся на общую теорию относительности Эйнштейна. Роль общей теории относительности для Небесной механики не ограничивается учётом малых поправок к теориям движения небесных тел. С появлением общей теории относительности удалось дать объяснение явлению тяготения, и таким образом Небесная механика как наука о гравитационном движении небесных тел по существу становится релятивистской. Согласно основной идее общей теории относительности, свойства пространства событий реального мира определяются движением и распределением масс, а движение и распределение масс, в свою очередь, определяются метрикой пространства-времени. Эта взаимосвязь находит своё отражение в уравнениях поля — нелинейных уравнениях с частными производными, определяющих метрику поля. В теории тяготения Ньютона уравнения движения (законы механики Ньютона) постулируются отдельно от уравнений поля. В общей же теории относительности уравнения движения тел содержатся в уравнениях поля.

Орбита пробной частицы при начальной скорости, равной 126 % от круговой скорости, и начальном удалении, равном 10 радиусам Шварцшильда.
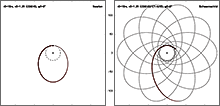
Слева: согласно ньютоновской механике, справа: согласно метрике Шварцшильда.

Релятивистские эффекты в движении больших планет Солнечной системы могут быть получены с достаточной точностью на основе решения Шварцшильда. Основным эффектом при этом является вековое смещение перигелиев планет. В решении Шварцшильда имеется также релятивистский вековой член в движении узла орбиты, но выделить этот эффект в явном виде из наблюдений не удаётся. Частично этот вековой член учитывается в радиолокационном эффекте при радиолокации Меркурия и Венеры с Земли (радиолокационный эффект состоит в дополнительном по сравнению с ньютоновским запаздыванием сигнала при возвращении его на Землю). Релятивистские эффекты в движении Луны получаются на основе решения релятивистской задачи трёх тел и обусловлены главным образом действием Солнца. Для усовершенствования теорий движения остальных естественных спутников планет достаточно к ньютоновой теории добавить релятивистские вековые члены в элементах орбит. Первая группа таких членов обусловлена шварцшильдовским смещением перицентра. Вторая группа — это вековые члены в долготе перицентра и узла, вызванные собственным вращением планеты. Движение планеты вокруг Солнца также приводит к вековым членам в этих элементах (геодезическая прецессия). Все эти члены для некоторых спутников могут достигать значительной величины (особенно для близких спутников Юпитера), но отсутствие точных наблюдений препятствует их обнаружению. Определение релятивистских эффектов в движении искусственных спутников Земли также не даёт положительных результатов из-за невозможности точного учёта влияния атмосферы и аномалий гравитационного поля Земли на их движение. Большой теоретический интерес представляют релятивистские поправки во вращательном движении небесных тел, однако, их обнаружение связано с ещё большими трудностями. Реальным представляется лишь выявление релятивистских эффектов при изучении прецессии гироскопов на Земле и на спутниках Земли.

Задачи небесной механики

Траектории двух тел разной массы, пребывающих в гравитационном взаимодействии друг с другом

Приблизительные траектории трёх одинаковых тел, находившихся в вершинах неравнобедренного треугольника и обладавших нулевыми начальными скоростями

Задачи разделяются на четыре большие группы:

1. Разработка общих вопросов движения небесных тел в гравитационном поле (так называемая задача N тел, частными случаями которой являются Задача трёх тел и Задача двух тел);
2. Построение математических теорий движения конкретных небесных тел как естественных, так и искусственных (планет, спутников, комет, космических зондов);
3. Сравнение теоретических исследований с астрономическими наблюдениями и определение таким путём числовых значений фундаментальных астрономических постоянных (элементы орбит; массы планет; постоянные, связанные с вращением Земли, характеризующие фигуру Земли и её гравитационное поле);
4. Составление астрономических эфемерид (Ежегодники астрономические), которые концентрируют в себе результаты теоретических исследований в области Небесной механики (а также астрометрии, звёздной астрономии, геодезии) и фиксируют на каждый момент времени фундаментальную пространственно-временную систему отсчёта, необходимую для всех разделов науки, имеющих дело с измерением пространства и времени.

Особый раздел задач, стоящих перед Небесной механикой, представляет изучение вращательного движения планет и спутников. Особо важное значение имеет теория вращения Земли, так как именно с Землёй связаны основные системы астрономических координат. Теория фигур планет возникла в Небесной механике, однако, в современной науке изучение фигуры Земли является предметом геодезии и геофизики, а строением других планет занимается астрофизика. Теория фигур планет и Луны стала особенно актуальной после запуска искусственных спутников Земли, Луны и Марса. Классической задачей Небесной механики является задача об устойчивости Солнечной системы. Проблема тесно связана с существованием вековых (непериодических) изменений больших полуосей, эксцентриситетов и наклонов планетных орбит. Методами небесной механики вопрос об устойчивости Солнечной системы не может быть полностью решён, так как математические ряды, используемые в задачах Небесной механики, пригодны только для ограниченного интервала времени. Уравнения Небесной механики не содержат такие малые факторы, как непрерывная потеря Солнцем его массы, которые, однако, могут играть существенную роль на больших интервалах времени. Тем не менее, отсутствие вековых возмущений первого и второго порядков у больших полуосей планетных орбит позволяет утверждать неизменность конфигурации Солнечной системы в течение нескольких миллионов лет.

Литература

Дубошин Г.Н. Небесная механика. Аналитические и качественные методы. — М.,: Наука, 1978.

Балк М.В., Демин В.Г., Куницын А.Л. Сборник задач по небесной механике и космодинамике. — М.,: Наука, 1972.