Конъюнкция

Конъюнкция
И, AND
Определение	$xy$
Таблица истинности	$(0001)$
Логический вентиль
Нормальные формы
Дизъюнктивная	$xy$
Конъюнктивная	$xy$
Полином Жегалкина	$xy$
Принадлежность предполным классам
Сохраняет 0	Да
Сохраняет 1	Да
Монотонна	Да
Линейна	Нет
Самодвойственна	Нет

Конъю́нкция (лат. conjunctio — «соединение») — логическая операция, выражающая соединение двух высказываний в сложное утверждение, истинное только в случае истинности всех составляющих элементов. В формальной логике и математике конъюнкция обозначается символами: ∧, &, · или соединительным союзом «и».

Формула конъюнкции для двух переменных

Высказывания A и B называются конъюнктивными членами высказывания A&B. Обозначение:

                                                                     $A\bigwedge B$

где A и B — логические переменные, принимающие значения «истина» (1) или «ложь» (0).

Для двух логических переменных A и B конъюнкция A ∧ B истинна тогда и только тогда, когда оба операнда истинны. В противном случае результат ложен. Здесь операнд — математический объект, на который действует оператор.

Свойства

Имеют место следующие свойства:

а) a ∧ b ≡ b ∧ a — коммутативный закон;

б) a ∧ 1 ≡ a — законы «1» для конъюнкции;

в) a ∧ 0 ≡ 0 — законы «0» для конъюнкции;

г) a ∧ a ≡ a — закон идемпотентности.

Таблица истинности

Значение истинности сложного конъюнктивного высказывания зависит от истинностных значений входящих в него простых высказываний и определяется на основе следующей таблицы истинности:

A	B	A∧B
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

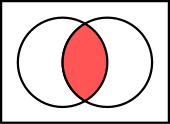
Связь с теорией множеств

Для любых двух множеств А и В определены новые множества, называемые объединением, пересечением, разностью и симметрической разностью. Конъюнкция аналогична операции пересечения множеств:

                                                             $A\bigcap B=\{x:x\in A\bigwedge x\in B\}$

то есть пересечение А и В есть множество всех таких х, что х — одновременно элемент А и элемент В.

Операции над множествами, введённые выше, соотносятся с логическими операциями следующим образом. Пусть А = {x: P(x)}, В = {x: Q(x)}, то есть множество А задано посредством характеристического предиката Р, а множество B — посредством характеристического предиката Q. Тогда:

                                                              $A\bigcap B=\{x:P(x)\bigwedge Q(x)\}$

Применение в различных областях

• Программирование:

В языках программирования Python оператор and используется для проверки нескольких условий. Чтобы проверить, что два условия истинны одновременно, объедините их ключевым словом and; если оба условия истинны, то и всё выражение тоже истинно. Если хотя бы одно (или оба) условия ложны, то и результат всего выражения равен False. Пример, в котором нужно убедиться, что каждому из двух людей больше 21 года:

>>> age_0 = 22

>>> age_1 = 18

>>> age_0 >= 21 and age_1 >= 21

False

>>> age_1 = 22

>>> age_0 >= 21 and age_1 >= 21

True

• Схемотехника

Логический элемент «И»

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах есть «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе есть «0»
  На иллюстрации приведён логический элемент И, имеющий два входа.

Особенности в естественном языке

• «Дважды два четыре, и снег бел». Для конъюнкции справедлив закон коммутативности: А&В эквивалентно B&А, хотя в высказываниях с союзом «и» этот закон действует далеко не всегда. Например, если в высказывании «Подул ветер, и деревья закачались» поменять местами члены конъюнкции, высказывание станет бессмысленным с точки зрения здравого смысла.
• Пусть р и q обозначают высказывания: p — «Джейн водит автомобиль», q — «У Боба русые волосы». Тогда сложное высказывание «Джейн водит автомобиль и у Боба русые волосы» состоит из двух частей, объединённых связкой и. Это высказывание может быть символически записано в виде p ∧ q.
• Если р — высказывание «Джон богат», а q — высказывание «Джон красив», то не знакомая с Джоном девушка, которую убедили в том, что высказывание «Джон богат и Джон красив», или «Джон богат и красив» истинно, будет представлять себе Джона и богатым, и красивым.