Кинематика

Устройство выбора роликов, разработанное в NX

Кинема́тика — это раздел механики, где изучают геометрические характеристики движения различных объектов, таких как материальные точки, системы точек, твёрдые тела и прочее. Основной упор делается на описание движения и формы объектов без учёта причин этого движения.

Ангел вращения вокруг неподвижной оси

История кинематики

Долгое время представления о кинематике были основаны на исследованиях Аристотеля. Учёный определял движение как любое изменение, благодаря которому происходит явление. Его широкое понимание движения позволяло считать, что в природе всё движется. Он различал локальное движение как частный вид изменения положения тела со временем, разделяя его на естественное и насильственное движения. Аристотель отрицал непрерывность и однородность явлений, утверждая, что движения зависят от того, происходят ли они по естественным или случайным причинам. Естественные движения могут быть прямолинейными, как, например, падение тяжёлых тел или подъём лёгких, либо круговыми, как движение звёзд вокруг Земли. Аристотель видел причину в регулярности и продолжительности кругового движения звёзд в неподвижном перводвигателе, который сообщал движение всем сферам, где находились звёзды с центром в центре Земли.

Вопреки общепринятому представлению, что земля находится в центре мироздания, далёкие звёзды вращаются вокруг неё. Аристотель вывел законы движения тел на земле из повседневного опыта, утверждая, что тяжёлые тела стремятся вниз, а лёгкие — вверх, и что все тела стремятся к своему естественному положению. Согласно его учениям, траектория падения или бросания тела состоит из трёх частей: наклонной прямолинейной, круговой и вертикальной прямолинейной. Эта концепция преобладала до 1546 года, и её динамика сильно отличалась от современной. По учениям Аристотеля движущееся тело постоянно подвергается воздействию какой-либо силы, его скорость пропорциональна приложенной силе и обратно пропорциональна сопротивлению среды. Это приводило к выводу, что в вакууме скорость была бы бесконечной, что противоречило обычным представлениям. Аристотель считал, что в природе не может существовать вакуум.

Учения Галилео Галилея. Опыт на Пизанской башне

Галилей считается основателем экспериментальной физики. Его эксперименты убедительно опровергли абстрактную метафизику Аристотеля и создали основы классической механики. Он доказал, что тяжёлые и лёгкие предметы падают вниз с одинаковой скоростью. Одним из известных мифов о Галилее является история, где он предположительно сбрасывал с Пизанской башни одновременно пушечное ядро массой 80 килограмм и мушкетную пулю массой 200 грамм, и оба предмета достигли земли одновременно. Однако все данные об этом эксперименте являются легендой и отсутствуют подтверждения его фактического проведения. Галилей понимал, что предметы разной формы и массы будут взаимодействовать с воздухом по-разному и не могут приземлиться одновременно. Несмотря на это, он вывел закон, что в отсутствии сопротивления все тела будут падать с одинаковой скоростью. Галилей предположил, что в вакууме все тела падают с одинаковым ускорением и вывел законы падения тел для идеального случая: тела, начавшие падать одновременно, двигаются с одинаковой скоростью и постоянным ускорением.

Учёные, выделившие отдельный раздел механики

Первые книги о механизмах появились в XV веке. В середине XVIII века была создана теоретическая основа для изучения механики. Французский учёный Жан Даламбер в своём труде «Динамика» (1743) высказал концепцию, что изучение механики должно начинаться с анализа движения самого по себе.

Эту идею дальше разработал петербургский академик Леонард Эйлер в своей известной «Теории движения твёрдых тел». Он предложил разделить изучение движения твёрдого тела на геометрическую и механическую части. Геометрический аспект проблемы, который не включает в себя причины движения, выделяют для аналитического определения перемещения, что упрощает подходы и поиск решений.

Идея выделения кинематики более чётко сформулирована Л. Карно, выдающийся деятель времён Великой французской революции. Андре Мари Ампер внёс понятие «кинематика», определяя её как науку, изучающую движения в окружающих телах и особенно в машинах. Кинематика рассматривается как часть теоретической механики и представляет изучение разнообразных движений и механизмов. Раздел кинематики был впервые чётко выделен в курсе «Физической и экспериментальной механики» генералом Понселе, прочитанном им в Парижском университете с 1837 по 1848 годы. Где он рассматривал различные аспекты движения, скорости, ускорения и различные типы механизмов, выделив кинематику как раздел теоретической механики.

Кинематика механизмов

Основные понятия кинематики

Кинематика — раздел механики, который изучает движение тела, не обращая внимания на его причины.

• Движение — это изменение положения тела в пространстве по мере прохождения времени.
• Тело отсчёта — это тело, относительно которого происходит анализ движения.
• При поступательном движении все точки тела перемещаются одинаково, сохраняя прямую линию, параллельную начальному положению в любой момент времени.
• Вращательное движение характеризуется тем, что все точки тела движутся по круговым траекториям, с центрами, расположенными на одной прямой, называемой осью вращения. Самое сложное движение может быть описано как комбинация поступательного и вращательного движения.
• Координаты — это числа, которые задают положение материальной точки в пространстве.
• Система координат — способ определения положения тела в пространстве с помощью числовых значений.
• Система отсчёта — это набор неподвижных тел (система отсчёта), связанных между собой, и часы (прибор), посредством которых изучается движение объектов относительно этой системы.
• Перемещение представляет собой вектор, проведённый от начального положения тела к конечному.
• Траектория — это путь, по которому движется тело, а путь является длиной данной траектории.

Задачи кинематики

Основной задачей является определение математического положения точек или объектов, находящихся в движении в течение времени. Каждое действие анализируется в определённой системе координат. Это направление рассматривает параллельные перемещения в различных системах отсчёта и определяет траекторию, учитывая зависимость скорости и ускорения от времени. При известных значениях скорости-координат в определённый момент времени считается, что движение полностью определено.

Другая задача заключается в разработке методов для расчёта положения всех кинематических параметров, характеризующих изменение положения точки или объекта.

Деление кинематики по типам объекта исследования

Кинематика механизмов

Кинематика твёрдого тела

Кинематика твёрдого тела исследует пять видов движения:

1. поступательное движение;
2. вращение вокруг неподвижной оси;
3. плоское движение;
4. движение вокруг неподвижной точки;
5. свободное движение.

Кинематика материальной точки

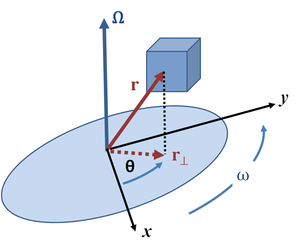
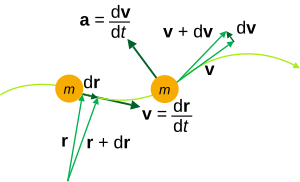
Движение материальной точки описывается относительно выбранной системы координат Oxyz. Кинематическими характеристиками движения точки являются векторы r, v и w, которые представляют собой мгновенное положение, скорость и ускорение точки в момент времени t соответственно: r(t) = {x(t), y(t), z(t)}, v(t) = dr/dt = {dx/dt, dy/dt, dz/dt} и w(t) = d²r/dt² = {d²x/dt², d²y/dt², d²z/dt²}. В кинематике помимо декартовых координат (x, y, z) используются также криволинейные координаты (цилиндрические, полярные, сферические и т. д.).

Геометрическое место последовательных положений точки во время её движения называется траекторией. Уравнение r = r(t) представляет параметрическую форму уравнения траектории как кривую в пространстве. Закон движения материальной точки также можно определить формой траектории, её положением в пространстве, положением начальной точки O на траектории и положительным направлением дуговой координаты s от начальной точки до её текущего значения. Уравнение s = s(t) определяет закон движения точки по траектории. Скорость материальной точки равна v = τ(ds/dt), где τ — единичный касательный вектор к траектории в точке M. В дифференциальной геометрии вводятся три взаимно перпендикулярных единичных вектора: τ, n (вектор главной нормали к кривой) и вектор бинормали β = [τ,n]. Векторы τ и n определяют касательную плоскость в точке M траектории.

Ускорение точки выражается формулой w(t) = dv/dt = d²r/dt² = τ(dv/dt) + nv²/R. Здесь полное ускорение точки представлено как сумма касательного ускорения w_τ (первое слагаемое) и центростремительного ускорения w_n (второе слагаемое), направленного вдоль главной нормали к траектории в сторону центра кривизны, расположенного на расстоянии R от точки M. Проекция вектора ускорения на бинормаль всегда равна нулю.

Для траектории, которая является прямой линией, в каждой её точке расстояние R = ∞; такое движение материальной точки называется прямолинейным. Если скорость материальной точки остаётся постоянной (v(t) = const ≠ 0), то это движение называется равномерным. Если касательное ускорение точки постоянно (dv/dt = const ≠ 0), то движение называется равноускоренным. Путь, который пройдёт точка в своём движении вдоль траектории, определяется как интеграл от модуля скорости по времени. Значение пути монотонно увеличивается, в то время как координата точки может как увеличиваться, так и уменьшаться. Например, в случае незатухающих колебаний математического маятника путь колеблющейся материальной точки непрерывно увеличивается, а её дуговая координата принимает значения, ограниченные амплитудой A колебаний (от -A до +A).

Кинематика относительного движения

Кинематика классической частицы массой m, положением r, скоростью v, ускорением a

Система координат Oxyz, относительно которой исследуется движение материальной точки M, может быть привязана к определённому телу, которое само движется относительно неподвижной системы

$$Ox_{1}y_{1}z_{1}.$$

В таком случае скорость и ускорение точки M относительно системы Oxyz называются относительными и обозначаются соответственно v_отн и w_отн. Движение той же материальной точки относительно системы $Ox_{1}y_{1}z_{1}$ называется абсолютным, а его скорость и ускорение обозначаются v_абс и w_абс.

Когда относительного движения нет (v_отн=0), точка M перемещается вместе с движущимся телом, к которому привязана система Oxyz, и её скорость совпадает со скоростью v_пер точки N тела, в которой находится точка M в данный момент времени: r_N(t)=r_M(t), но это не совпадение (поскольку это относится к независимым точкам). Вектор v_пер=drN/dt называется скоростью переноса или скоростью перемещения. Формула v_абс=v_отн+v_пер представляет собой так называемую теорему сложения скоростей. Ускорение точки N называется переносным и обозначается w_пер. Суммирование ускорений описывается теоремой Кориолиса: w_абс=w_отн+w_пер+w_Кор. Здесь дополнительное слагаемое w_Кор (ускорение Кориолиса) появляется, когда система Oxyz вращается относительно системы $Ox_{1}y_{1}z_{1}$: w_Кор=2[ω,v_отн], где ω — вектор угловой скорости подвижной системы координат.

Поступательное и вращательное движения считаются основными видами движения твёрдого тела. Данное движение означает, что любой выбранный в теле отрезок остаётся параллельным самому себе со временем. При рассмотрении поступательного движения твёрдого тела число степеней свободы тела обычно равно трём, так как описание движения одной точки тела, например точки A, в декартовой системе координат, достаточно. Траектории остальных точек могут быть получены путём «параллельного» перемещения в пространстве. При поступательном движении все точки твёрдого тела перемещаются на одно и то же расстояние за одинаковый промежуток времени. Поэтому скорости и ускорения всех точек тела в определённый момент времени одинаковы. Поступательное движение твёрдого тела может быть полностью описано, если известна зависимость радиус-вектора r(t) движения любой точки этого тела от времени и его начальное положение.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!