Закон Ома
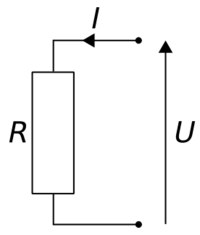
Зако́н О́ма - закон электротехники, открытый в 1826 году немецким учёным Георгом Омом, который описывает линейную зависимость между силой тока на участке цепи и электрическим напряжением на этом участке. Впервые был опубликован в 1827 году, после чего закон получил своё название в честь исследовавшего его учёного. Заслуга Ома заключалась в том, что он ввёл понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи. Для участка цепи закон Ома представлен формулой[1][2]:
- , где
- — сила тока в цепи, А;
- — электрическое напряжение на участке цепи, В;
- — электрическое сопротивление участка цепи, Ом;
Закон Ома применим для цепей, в которых сопротивление является постоянным. Звучит закон Ома так:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Для неоднородного участка цепи, который содержит источник ЭДС закон Ома также может быть записан формулой, которая использует определение электрического напряжения как суммы ЭДС, действующей на выбранном участке цепи между двумя заданными точками, и разность потенциалов между этими точками. Эту формулу называют обобщенным законом Ома для участка цепи[3][4]:
Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих ЭДС), так и для активных. Для замкнутого участка цепи, в которой точки 1 и 2 совпадают φ1 = φ2, а значит формула, приведённая выше, упрощается до[1][4]:
Закон Ома не всегда применим для всех элементов электрической цепи. Если на участке цепи задействованы нелинейные элементы - диоды и транзисторы, то прямая пропорциональность между силой тока и напряжением теряется[5].
Области применения
Закон Ома применяется во всех отраслях электротехники, так как позволяет рассчитывать ток или напряжение на определенных участках цепи, а также определить необходимые значения сопротивления для построения моделей с желаемыми параметрами, но в электродинамике сплошных сред и в теории электрических цепей имеет несколько разный смысл и область применения.
В физике закон Ома — изначально эмпирическое соотношение, которое было впоследствии объяснено теорией Друде о движении электронов в металлах. Это соотношение хорошо описывает часто встречаемые на практике типы проводников в квазистационарном приближении, но не является фундаментальным физическим законом и перестаёт соблюдаться в ряде ситуаций.
В теории электрических цепей закон Ома аксиоматически определяет связь параметров напряжения и тока в модели электрической цепи через параметр электрического сопротивления (или, в общем случае, через параметр комплексного импеданса). Существуют законы Ома для комплексных амплитуд и для комплексных действующих значений[6].
История
В 1825—1827 годах Георг Ом проводил опыты с источником ЭДС в виде термопары, гальванометром и металлической проволокой. Он обнаружил, что сила тока через проволоку в его опытах хорошо описывается линейным законом на основе трёх параметров, и в 1827 году опубликовал результаты в виде работы Die galvanische Kette, mathematisch bearbeitet[7]. Опыты Георга Ома проводились до зарождения теории цепей и правил Кирхгофа (1845—1847), теории электромагнитного поля (1864), уравнений Максвелла (1884), и теории Друде (1900). В его работе закон Ома был записан как выражение
- , где:
- — показания гальванометра (в современных терминах — сила тока);
- — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современных терминах — ЭДС);
- — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока r).
- — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи R).
Позднее, в 1845—1849 годах Густав Кирхгоф предложил корректную физическую интерпретацию этих величин, и в 1849 году опубликовал работу, включающую в себя закон Ома в современных единицах[8].
Оригинальная формула при использовании современных терминов выражает так называемый закон Ома для полной цепи:
- , где:
- — ЭДС источника, В;
- — сила тока в цепи, А;
- — сопротивление всех элементов цепи (не включая источник ЭДС), Ом;
- — внутреннее сопротивление источника ЭДС, Ом.
Закон Ома в дифференциальной форме
Линейная связь плотности тока и напряжённости электрического поля в некоторой точке проводника описывается законом Ома в дифференциальной форме. Коэффициентом пропорциональности является удельная проводимость материала. Для изотропных материалов дифференциальная форма закона Ома выглядит как:
где:
- — вектор плотности тока;
- — удельная электрическая проводимость ();
- — вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени.
В классическом приближении закон Ома в дифференциальной форме можно вывести с использованием теории Друде:
где:
- — удельная электрическая проводимость ();
- — концентрация электронов;
- — элементарный заряд;
- — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
- — эффективная масса электрона.
Такими формулами пользуются для вычисления тока и сопротивления утечки кабеля и цилиндрического конденсатора.
Закон Ома для переменного тока
В теории электрических цепей закон Ома обобщается для переменного тока. Специальному рассмотрению подлежит лишь учёт фазового сдвига между током и напряжением. Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), закон Ома может быть записан в комплексных величинах:
где:
- — комплексное напряжение,
- — комплексная сила тока,
- — комплексное сопротивление (электрический импеданс),
- R = √Ra2 + Rr2 — полное сопротивление (модуль импеданса),
- Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока (фаза импеданса, с точностью до обратного знака).
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению гармоник (колебаний с частотой, кратной частоте тока, действующего на цепь), а также колебаний с суммарными и разностными частотами. Вследствие этого закон Ома в нелинейных цепях, вообще говоря, не выполняется.
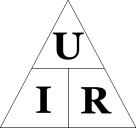
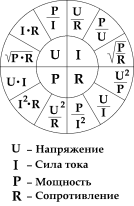
Мнемоническая диаграмма для закона Ома
Соотношение между различными величинами в законе Ома часто схематично показывают в виде треугольника, который называется треугольником закона Ома или его мнемонической диаграммой. Этот метод описания прост для запоминания правила соотношения между напряжением, током и сопротивлением. Согласно мнемонической диаграмме можно получить выражение для необходимой величины из формулы закона Ома: если закрыть искомую величину, и два других символа дадут формулу для её вычисления[9][10].
Практическое значение закона Ома
Закон Ома демонстрирует, что при высоком сопротивлении ток будет низким, но когда сопротивление низкое, ток будет высоким при любом приложенном напряжении. Этот постулат имеет большую практическую ценность, так как одна из трудностей при проектировании высоковольтных линий электропередач (ЛЭП) является уменьшение потерь при доставке энергии к потребителю. Эти потери проявляются в переходе энергии тока в тепловую энергию, то есть в нагреве проводов. Таким образом, перед проектировщиками стоит задача довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи где где - суммарное сопротивление проводов и внутреннего сопротивления генератора, которое необходимо учитывать даже при условии, его сопротивления значительно меньше сопротивления линии передач[10].
В таком случае потери мощности будут определяться выражением
При постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.
Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.
Ограничения применимости закона Ома
Закон Ома (как физический закон) может не соблюдаться:
- Для любых сред, к которым не применима теория Друде (например, плазма или вакуум)
- При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
- При низких температурах для веществ, обладающих сверхпроводимостью.
- При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
- При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
- В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
- В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
- В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике)[11].
Примечания
- ↑ 1,0 1,1 Ю. В. Юрьев. Закон Ома. Большая Российская Энциклопедия. Дата обращения: 13 октября 2023.
- ↑ Б. Михеев, Н. Герасимов. Закон Ома // Комсомольская правда : газета.
- ↑ Ю. В. Юрьев. Электрическое напряжение. Большая российская энциклопедия. Дата обращения: 13 октября 2023.
- ↑ 4,0 4,1 Д. В. Сивухин. Общий курс физики. Учеб. пособие: Для вузов. В 5 т. Т. III. Электричество. — Москва: Физматлит: издательство МФТИ, 2004. — С. 194. — ISBN 5-9221-0227-3.
- ↑ Закон Ома: основные принципы и применение в электротехнике. Деметра Л. Дата обращения: 20 ноября 2023.
- ↑ Матвиенко В.А. Основы теории цепей : учебное пособие для вузов. — Екатеринбург: УМЦ УПИ, 2016. — С. 52. — ISBN 978-5-8295-0425-0.
- ↑ G. S. Ohm (1827). Die galvanische Kette, mathematisch bearbeitet. Berlin: T. H. Riemann.. Дата обращения: 13 октября 2023.
- ↑ Franco Maloberti, Anthony C. Davies. A Short History of Circuits and Systems. — Denmark: River Publishers, 2016. — ISBN 978-87-93379-70-1.
- ↑ Закон Ома в интегральной и дифференциальной форме Источник: https://electric-220.ru/zakon-oma-v-integralnoj-i-differentsialnoj-forme. Дата обращения: 13 октября 2023.
- ↑ 10,0 10,1 Электрическая мощность и закон Ома. Дата обращения: 20 ноября 2023.
- ↑ Рез И. С., Поплавко Ю. М. Диэлектрики. Основные свойства и применения в электронике. — М., Радио и связь, 1989, — с. 46-51
Ссылки
- Закон Ома // Элементы.ru. Природа науки, Энциклопедия