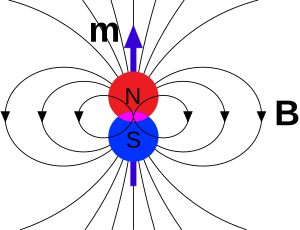
Магнитная индукция

Магнитная индукция
Магнитная индукция
Размерность	MT−2I−1
Единицы измерения
СИ	Тл
СГС	Гс

Магни́тная инду́кция — векторная физическая величина, являющаяся силовой характеристикой магнитного поля, а именно характеристикой его действия на движущиеся заряженные частицы и на обладающие магнитным моментом тела. Выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля^[1].

Стандартное обозначение: ${\vec {B}}$ .

Единицы измерения:

в СИ — тесла (Тл),

в СГС — гаусс (Гс) (соотношение размерностей: 1 Тл = 10⁴ Гс).

Величина магнитной индукции фигурирует в ряде важнейших формул электродинамики, включая уравнения Максвелла^[2].

Физический смысл

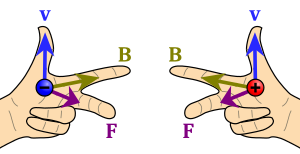
Правила для магнитных сил, действующих на отрицательно (слева) и положительно заряженные частицы (справа).

Магнитная индукция ${\vec {B}}$ характеризуется тем, что сила Лоренца ${\vec {F}}$ , действующая со стороны магнитного поля на заряд $q^{*}$ , движущийся со скоростью ${\vec {v}}$ , равна

{\vec {F}}=q^{*}\left[{\vec {v}}\times {\vec {B}}\right]

(по величине

F=q^{*}vB\sin \alpha

).

В приведённой формуле символом ( $\times$ ) обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (вектор ${\vec {F}}$ перпендикулярен им обоим и направлен по правилу левой руки для отрицательно заряженных частиц и правилу правой руки для частиц с положительным зарядом)^{[сп. 1]}^[3].

Также магнитная индукция может быть определена как отношение максимального механического момента сил, действующих на рамку с током, помещённую в предполагаемое однородным (на расстояниях порядка размера рамки) магнитное поле, к произведению силы тока $I^{*}$ в рамке на её площадь^{[сп. 2]}. Момент сил зависит от ориентации рамки и достигает максимального значения при каких-то определённых углах. Звёздочка у символа указывает на то, что заряд или ток являются «пробными^{[сп. 3]}», то есть используемыми именно для регистрации поля, в отличие от тех же величин без звёздочки.

Магнитная индукция выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля ${\vec {E}}$ .

Способы расчёта

Общий случай

В общем случае расчёт магнитной индукции проводится посредством решения системы уравнений Максвелла совместно с расчётом электрической составляющей электромагнитного поля:

Невозможно разобрать выражение (синтаксическая ошибка): {\displaystyle \mathrm{div}\,(\varepsilon\vec E) = \frac{\rho}{\varepsilon_0},\ \ \ \mathrm{rot}\,\vec E = - \frac{\partial \vec B}{\partial t}, }

\mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\frac {\vec {B}}{\mu }}=\mu _{0}{\vec {j}}+{\frac {\varepsilon }{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}

,

где $\mu _{0}$ — магнитная постоянная, $\mu$ — магнитная проницаемость, $\varepsilon$ — диэлектрическая проницаемость, а $c$ — скорость света в вакууме. Через $\rho$ обозначена плотность заряда (Кл/м³) и через ${\vec {j}}$ плотность тока (А/м²).

Магнитостатика

Магнитное поле вокруг проводника с током

Магнитное поле соленоида

Магнитное поле постоянного магнита

В магнитостатическом пределе^{[сп. 4]} расчёт магнитного поля может быть выполнен с использованием формулы Био—Савара—Лапласа. Вид этой формулы несколько различен для ситуаций, когда поле создаётся текущим по проводу $L_{1}$ током $I$ или когда оно создаётся объёмным распределением тока:

{\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right)d{\vec {l}}_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},\qquad {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}}

.

В магнитостатике эта формула играет ту же роль, что и закон Кулона в электростатике. Формула позволяет вычислить магнитную индукцию в вакууме. Для случая магнитной среды необходимо использовать уравнения Максвелла (без слагаемых с производными по времени)^[4].

Если заранее очевидна геометрия поля, применима теорема Ампера о циркуляции магнитного поля^{[сп. 5]} (эта запись является интегральной формой уравнения Максвелла для $\mathrm {rot} \,{\vec {B}}$ в вакууме):

\oint \limits _{L}{\vec {B}}\cdot d{\vec {l}}=\mu _{0}\int \limits _{S}{\vec {j}}\cdot d{\vec {S}}

.

Здесь $S$ — произвольная поверхность, «натянутая» на выбранный замкнутый контур $L$ .

Простые примеры

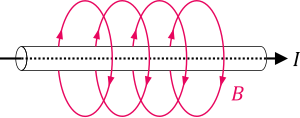
Вектор магнитной индукции прямого провода с током $I$ на расстоянии $a$ от него составляет

{\vec {B}}={\frac {\mu _{0}\mu I}{2\pi a}}\cdot {\vec {e}}_{\varphi }

,

где ${\vec {e}}_{\varphi }$ — единичный вектор вдоль окружности, по оси симметрии которой проложен провод. Предполагается, что среда однородна.

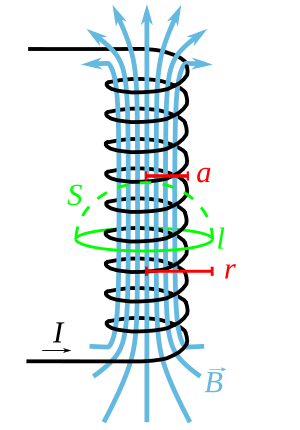
Вектор магнитной индукции прямого внутри соленоида с током $I$ и числом витков на единицу длины $n$ равен

{\vec {B}}=\mu _{0}\mu nI\cdot {\vec {e}}_{z}

,

где ${\vec {e}}_{z}$ — единичный вектор вдоль оси соленоида. Здесь также предполагается однородность магнетика, которым заполнен соленоид.

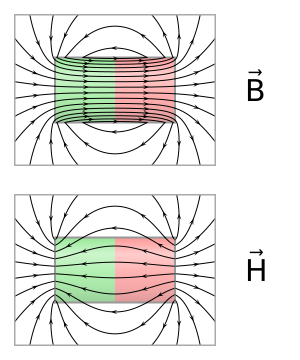
Связь с напряжённостью

Магнитная индукция и напряжённость магнитного поля связаны через соотношение

{\vec {B}}=\mu _{0}\mu {\vec {H}}

,

где $\mu$ — магнитная проницаемость среды (в общем случае это тензорная величина, но в большинстве реальных случаев её можно считать скаляром, то есть просто константой конкретного материала).

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в большое число уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, — это электростатика.

Некоторые из уравнений:

Три из выписанных выше четырех уравнений Максвелла (основных уравнений электродинамики)^[5]. Их физическое содержание:
1. уравнение для $\mathrm {div} \,{\vec {B}}$ — закон отсутствия монополя,
2. для $\mathrm {rot} \,{\vec {E}}$ — закон электромагнитной индукции Фарадея,
3. для $\mathrm {rot} \,{\vec {B}}$ — закон Ампера — Максвелла.
Формула силы Лоренца при наличии и магнитного ( ${\vec {B}}$ ), и электрического ( ${\vec {E}}$ ) поля:
${\vec {F}}=q^{*}{\vec {E}}+q^{*}\left[{\vec {v}}\times {\vec {B}}\right]$ .
Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)^{[сп. 6]}:
$d{\vec {F}}=\left[I^{*}{\vec {dl}}\times {\vec {B}}\right]$ или $d{\vec {F}}=\left[{\vec {j}}^{*}dV\times {\vec {B}}\right]$ .

Магнитный диполь, состоящий из двух магнитных зарядов (монополей).

Ориентация магнитного диполя во внешнем магнитном поле.

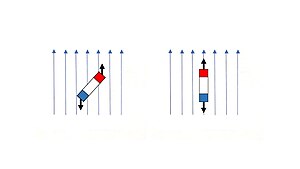
Выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь $m^{*}$ (виток с током, катушку или постоянный магнит):
${\vec {M}}={\vec {m}}^{*}\times {\vec {B}}$ .
Выражение для потенциальной энергии магнитного диполя в магнитном поле:
$U=-{\vec {m}}^{*}\cdot {\vec {B}}$ ,

из которого следуют выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле,

Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд^{[сп. 7]}:
${\vec {F}}=K{\frac {q_{m}^{*}{\vec {r}}}{r^{3}}}.$

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено. Оно также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля
$w={\frac {B^{2}}{2\mu _{0}\mu }}$ .

Оно входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля, и в лагранжиан электромагнитного поля, и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Типичные значения

Характерные значения магнитной индукции
Объект	Тл	Объект	Тл
межзвёздное пространство	10^-10	небольшой магнит (Nd-Fe-B)	0,2
магнитное поле Земли	5 • 10^-5	большой электромагнит	1,5
1 см от провода с током 100 А	2 • 10^-3	сильный лабораторный магнит	10
небольшой магнит (феррит)	0,01	поверхность нейтронной звезды	10⁸

Литература

Коваленко И. И. Курс физики: учебное пособие. Электричество и магнетизм. — СПб.: ГУАП, 2020. — 143 с. — ISBN 978-5-8088-1480-6.

Примечания

Справка

↑ Если учитывать и действие электрического поля ${\vec {E}}$ , то формула (полной) силы Лоренца принимает вид:
${\vec {F}}=q^{*}{\vec {E}}+q^{*}[{\vec {v}}\times {\vec {B}}].$
При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведённую в основном тексте.
↑ Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако может быть полезным как один из практических способов измерения магнитной индукции, а также с исторической точки зрения.
↑ Пробный заряд — это точечный заряд, достаточно малый по величине, чтобы своим присутствием он не мог изменить внешнее по отношению к нему поле. Пробный ток – ток, существующий в плоском контуре малых размеров.
↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.
↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла.
↑ Сила, действующая на провод, по которому проходит ток, аналогична силе, действующей на движущийся заряд, поскольку провод, по которому проходит ток, можно рассматривать как совокупность движущихся зарядов.
↑ Магнитный заряд (монополь) — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля.

Источники

↑ Магнитная индукция (неопр.). Большая Российская энциклопедия. Дата обращения: 21 марта 2025.
↑ Магнитная индукция // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Лоренца сила // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик и др. — М.: Советская энциклопедия, 1983. — С. 383. — 928 с. — 100 000 экз.
↑ Уравнения Максвелла // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Ссылки

[autogenerated1-3] Если учитывать и действие электрического поля ${\vec {E}}$ , то формула (полной) силы Лоренца принимает вид:
${\vec {F}}=q^{*}{\vec {E}}+q^{*}[{\vec {v}}\times {\vec {B}}].$
При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведённую в основном тексте.

[autogenerated2-5] Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако может быть полезным как один из практических способов измерения магнитной индукции, а также с исторической точки зрения.

[autogenerated3-6] Пробный заряд — это точечный заряд, достаточно малый по величине, чтобы своим присутствием он не мог изменить внешнее по отношению к нему поле. Пробный ток – ток, существующий в плоском контуре малых размеров.

[autogenerated4-7] То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.

[autogenerated5-9] Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла.

[autogenerated6-11] Сила, действующая на провод, по которому проходит ток, аналогична силе, действующей на движущийся заряд, поскольку провод, по которому проходит ток, можно рассматривать как совокупность движущихся зарядов.

[autogenerated7-12] Магнитный заряд (монополь) — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля.

[1] Магнитная индукция (неопр.). Большая Российская энциклопедия. Дата обращения: 21 марта 2025.

[2] Магнитная индукция // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.

[4] Лоренца сила // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.

[8] Физический энциклопедический словарь / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик и др. — М.: Советская энциклопедия, 1983. — С. 383. — 928 с. — 100 000 экз.

[10] Уравнения Максвелла // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

[1]

[2]

[сп. 1]

[3]

[сп. 2]

[сп. 3]

[сп. 4]

[4]

[сп. 5]

[5]

[сп. 6]

[сп. 7]