Проекция Меркатора

Карта мира Меркатора 1569 года.

Прое́́кция Мерка́тора — предложенная в 1569 году фламандским картографом Герардом Кремером (латинизированное имя Герардус Меркатор) картографическая проекция, предложенная для составления карты мира размером 101 на 124 см на 18 листах (3 по вертикали и 6 по горизонтали). Проекция очень понравилась морякам, поскольку позволяла легко прокладывать по карте курс в море и держать его, оттого проекция до настоящего времени применяется для составления морских и аэронавигационных карт.

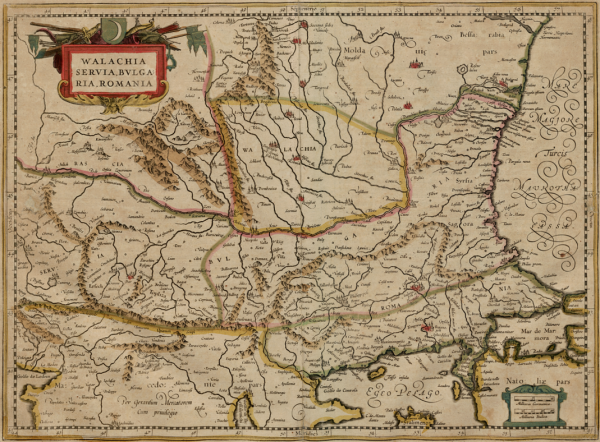
Фундаментальный труд Меркатора — Атлас мира

Завершив обучение в гимназии и продолжив обучение в одном из лучших университетов Северной Европы в городе Лёвене, Меркатор (уже сменивший к тому времени фамилию) учится чертить карты, делать глобусы и изготавливать географические инструменты под руководством нидерландского учёного и мастера астрономических инструментов Геммы Фризиуса. Года обучения ему хватило, чтобы начать работать самостоятельно и выпускать географические карты.

С трудом избежав обвинения в еретичестве и отсидев свыше полугода в замке, Меркатор оседает в итоге в Дуйсбурге, где продолжает составлять карты. Атлас мира — наиболее фундаментальный труд Меркатора, вышедший в печатном варианте через 4 года после его смерти в возрасте 82 лет, в 1594 году, и объединяющий 51 карту. В атласе использовались самые разные картографические проекции, ниже представлена одна из карт Атласа 1589 года в проекции Меркатора..

Карта Валахии, Сербии, Болгарии и Румынии в проекции Меркатора.

При рассмотрении картографической сетки карты (изображенных на карте линий меридианов и параллелей, отражающих значения долгот и широт), бросается в глаза, что расстояние между одним градусом по широте примерно в 1,5 раза больше расстояние между одним градусом по долготе. Это и есть особенность предложенной Меркатором проекции — растянутость карты по вертикали.

Построение картографической сетки в проекции Меркатора

Герардус Меркатор.

Генрих Мореплаватель.

Проекция Меркатора является цилиндрической нормальной равноугольной на касательном цилиндре. Но эта проекция не является перспективной (то есть не получена путем проекции), хотя её часто путают с перспективной центральной цилиндрической проекцией (совершенно непрактичной и не нашедшей применения вследствие неприемлемых вертикальных искажений).

Метод, благодаря которому Меркатор пришел к принципу построения своих карт, неизвестен, но название, данное Меркатором 18-листовой карте мира «Новое и дополненное описание Земли, исправленное для использования моряками», проясняет, что автор проекции сознавал основное назначение карт в предложенной им проекции. Математическое описание проекции Меркатора дал в 1599 году (и более подробно в 1610 году) английский математик Эдвард Райт (1561—1615).

Чтобы получить карту Земли в проекции Меркатора, то есть отобразить поверхность глобуса на плоскости, необходимо поместить глобус внутрь касательного цилиндра, касающегося глобуса по экватору. Если из центра глобуса спроектировать меридианы на внутренние стенки цилиндра, они отобразятся в виде прямых вертикальных линий, перпендикулярных экватору (отображаемому горизонтальной прямой линией).

При этом параллели, если между ними сохранить расстояния, равные расстояниям между ними на глобусе, отобразятся в виде сетки параллельных линий, но длина каждой из параллелей окажется равной длине экватора, то есть все параллели растянутся, и степень растяжения будет тем больше, чем больше широта рассматриваемой параллели.

В итоге получена некоторая проекция, отличная от проекции Меркатора, и называемая цилиндрической квадратной проекцией на прямом касательном цилиндре. Эта проекция, называемая также простой равнопромежуточной цилиндрической, была предложена в 1438 году, за 131 год до Меркатора, португальским принцем Генрихом, известном как Генрих Мореплаватель (1394—1460). По факту, эта проекция была известна еще древнегреческому математику Эратосфену (276 −194 до н. э.).

Карта мира в проекции Генриха Мореплавателя.

В данной проекции поверхность Земли отображается прямоугольником шириной вдвое выше высоты, при этом Северный и Южный географические полюса растягиваются до горизонтальных линий, ограничивающих карту сверху и снизу.

Из геометрических соображений следует, что поскольку (при принятии модели шарообразной Земли) длина параллели пропорциональна косинусу широты параллели φ, при растяжении (на карте) параллели до длины экватора, показатель искажения длины для проекции Генриха Мореплавателя по горизонтали составляет $n={\frac {1}{\cos {\psi }}}$ . Показатель искажения по вертикали по определению равен единице, $m=1$ , то есть искажения отсутствуют. Показатель искажения площадей p, равный произведению показателей искажений по вертикали и горизонтали, составляет $p=mn={\frac {1}{\cos {\psi }}}$ .

Но проекция Меркатора является равноугольной (что означает, что линейные искажения по горизонтали и вертикали равны), и для выполнения этого условия необходимо растягивать карту по вертикали таким образом, чтобы вертикальные расстояния между параллелями увеличивались согласно растяжению данных параллелей по горизонтали, лишь в этом случае будут сохранены углы между направлениями и сохранится форма малых фигур.

Карта мира в проекции Меркатора

При равенстве показателя горизонтальных искажений $n={\frac {1}{\cos {\psi }}}$ , показатель вертикальных искажений m должен равняться этой же величине, $m=n={\frac {1}{\cos {\psi }}}$ , а показатель искажения площадей составит $p=mn={\frac {1}{\cos ^{2}{\psi }}}$ .

При практическом построении сетки меридианов и параллелей необходимо знать, по какому закону рассчитывается удаление каждой параллели по меридиану от экватора. Если в проекции Генриха Мореплавателя расстояние каждой параллели от экватора пропорционально её широте, то в проекции Меркатора эти расстояния увеличиваются в $\ln {(\tan {(45^{\circ }+\psi /2)})}$ раз.

Сказанное поясняется рисунком с принципами построения картографической сетки двух сравниваемых проекций.

Принципы построения картографической сетки по двум сравниваемым проекциям.

В таблице приведены величины искажений по вертикали m, искажений по горизонтали n, по площадям p, коэффициенты k увеличения расстояний параллелей от экватора в проекции Меркатора в сравнении с проекцией Генриха Мореплавателя и условные величины удаления параллелей от экватора L, исходя из того, что за единицу расстояния принято расстояние на карте, соответствующее в масштабе одному градусу долготы по экватору.


	Проекция Генриха Мореплавателя				Проекция Меркатора
	m	n	p	L	m	n	p	k	L
0	1	1,00	1,00	0	1,00	1,00	1,00	1,00	0,00
10	1	1,02	1,02	10	1,02	1,02	1,03	1,01	10,05
20	1	1,06	1,06	20	1,06	1,06	1,13	1,02	20,42
30	1	1,15	1,15	30	1,15	1,15	1,33	1,05	31,47
40	1	1,31	1,31	40	1,31	1,31	1,70	1,09	43,71
50	1	1,56	1,56	50	1,56	1,56	2,42	1,16	57,91
60	1	2,00	2,00	60	2,00	2,00	4,00	1,26	75,46
70	1	2,92	2,92	70	2,92	2,92	8,55	1,42	99,43
80	1	5,76	5,76	80	5,76	5,76	33,16	1,74	139,59
90	1			90

Ввиду того, что карта мира в проекции Меркатора растягивается по вертикали, обычно области с широтами выше 80-95° северной и южной широты на картах не изображаются.

Достоинства и недостатки карт в проекции Меркатора

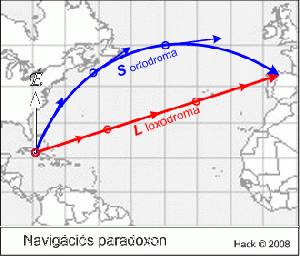
При прокладке в море пути между двумя точками проще всего приложить на карте линейку к пункту отправления и пункту назначения, и провести прямую линию. Но если карта будет не в одной из равноугольных проекций, проведенная по карте линия будет пересекать меридианы под разными углами, что означает, что в пути придется непрерывно менять курс судна. А вот если карта составлена в проекции Меркатора, линия пересекает все меридианы под равными углами, что позволяет держать курс судна неизменным весь путь следования. Это обстоятельство и сделало проекцию Меркатора удобной для построения морских карт.

Кривая на поверхности Земли (или глобуса), пересекающая все меридианы под постоянным углом, называется локсодромой или локсодромией. Локсодрома не является кратчайшим путем между двумя точками (кратчайший путь называется ортодромой или ортодромией, и представляет собой дугу большого круга), но движение по ортодроме осуществляется с постоянным изменением курса судна, что требует особых расчетов, а также знания точного положения судна в море, что было невозможно в те времена, когда еще не умели точно определять долготу судна (что стало возможным лишь с изобретением морского хронометра в 1736 году).

Движение же по локсодромии не требует знания долготы, достаточно было плыть, держась постоянного курса, и ждать возгласа смотрящего матроса с мачты «Земля!».

Движение по локсодромии (красная линия) и ортодромии (синяя линия).

Недостатком проекции Меркатора является разный масштаб по экватору и параллелям, к достоинству следует отнести равенство масштаба по вертикали и горизонтали в каждой точке карты, что позволяет сохранять форму отдельных объектов (например, островов). Так, Гренландия на картах в проекции Генриха Мореплавателя растянута по горизонтали, что не позволяет составить представление об её истинной форме. На картах в проекции Меркатора Гренландия изображается с огромным искажением масштаба, выглядит значительно больше своего истинного размера, но при этом сохраняет свою форму.

При всех недостатках проекции Меркатора при создании карт больших участков поверхности, она легла в основу системы UTM (англ. Universal Transverse Mercator — универсальная поперечная проекция Меркатора). Эта система используется при составлении карт большого масштаба, то есть карт участков небольшой протяженности.

Применявшаяся в СССР и ряде других стран (и сохраненная в современной России) для составления топографических карт равноугольная поперечная цилиндрическая проекция Гаусса-Крюгера является вариантом поперечной проекции Меркатора (в которой цилиндр ориентирован не вдоль экватора, а вдоль одного из меридианов — среднего меридиана зоны). В этой проекции поверхность земного шара (рассматриваемого как эллипсоид), делится на 60 шестиградусных или 120 трехградусных зон, ограниченные меридианами от полюса до полюса.

Ниже представлен рисунок, поясняющий принцип построения карт в проекции Гаусса-Крюгера.

Поперечная проекция Меркатора с делением Земли на 6 60-градусных зон.

Примерно с 1940-х годов проекция Меркатора в атласах перестала использоваться, ей на смену пришли более современные проекции, одна из которых тройная проекция Винкеля, компромиссная по совокупности искажений.

Литература

Картоведение: Учебник для вузов / А. М. Берлянт, А. В. Востокова, В. И. Кравцов а и др.; Под ред. А. М. Берлянт — М.: Аспект Пресс, 2003.— 477 с. — (серия «Классический университетский учебник»). ISBN 5-7567-0304-7
Вахрамеева Л. А., Бугаевский Л. М., Казакова 3. Л. Математическая картография: Учебник для вузов.— М.: Недра, 1986.— 286 с.
Проекция Меркатора. — Квантик. — № 7. — 2015. (Геодезия и картография.)

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!