Сортировка выбором
Сортиро́вка вы́бором — это алгоритм сортировки с O(n²) временной сложностью, что делает его неэффективным для больших списков (как правило справляется с задачей хуже, чем алгоритм сортировки вставками[1]. Тем не менее, сортировка выбором отмечается своей простотой и имеет преимущества в производительности перед более сложными алгоритмами в определенных ситуациях, особенно когда объем используемой памяти ограничен.
Описание алгоритма
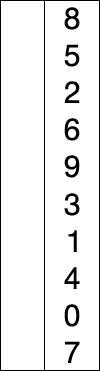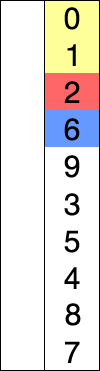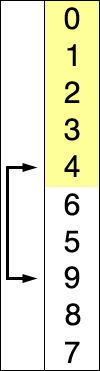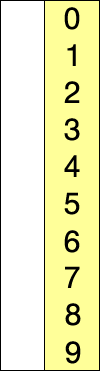
Алгоритм разделяет входной список на две части[1]: отсортированный подсписок элементов, который строится слева направо в начале (слева) списка, и подсписок оставшихся неотсортированных элементов, занимающих остальную часть списка. Изначально отсортированный подсписок пуст, а неотсортированный подсписок — это весь входной список. Алгоритм продолжает находить самый маленький (или самый большой, в зависимости от порядка сортировки) элемент в неотсортированном подсписке, обменивать его с самым левым неотсортированным элементом (приводя его в отсортированный порядок), и перемещать границы подсписков на один элемент вправо.
Пример работы
Вот пример этого алгоритма сортировки для пяти элементов[1]:
| Отсортированный подсписок | Неотсортированный подсписок | Наименьший элемент в неотсортированном списке |
|---|---|---|
| () | (12, 25, 64, 11, 22) | 11 |
| (11) | (25, 64, 12, 22) | 12 |
| (11, 12) | (64, 25, 22) | 22 |
| (11, 12, 22) | (25, 64) | 25 |
| (11, 12, 22, 25) | (64) | 64 |
| (11, 12, 22, 25, 64) | () |
(В последних двух строках ничего не меняется, потому что последние два числа уже были в нужном порядке.)
Сортировка выбором также может использоваться со структурами данных, которые эффективно поддерживают добавление и удаление, такими как связанный список. В этом случае чаще всего минимальный элемент удаляется из неотсортированной части списка, а затем вставляется в конец отсортированных значений.
Реализации
Приведенный ниже код демонстрирует реализацию сортировки выбором на языке Python:
def selection_sort(arr):
for i in range(len(arr)):
min_index = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
Сложность
- Временная сложность: В худшем случае O(n²), где n — количество элементов в массиве. Это происходит потому, что каждый элемент сравнивается со всеми остальными [2].
- Пространственная сложность: O(1). Алгоритм требует только постоянного дополнительного места для хранения переменных.
Преимущества и недостатки
Преимущества
Недостатки
- Высокая временная сложность для больших массивов.
- Несколько обменов данных могут быть затратными по времени[2].
Использование и критика
Сортировка выбором находит применение в учебных целях и для обработки небольших массивов данных, где её простота реализации становится преимуществом. Она особенно полезна для начинающих программистов, так как помогает понять основные принципы работы алгоритмов сортировки без сложных оптимизаций. Однако на практике этот метод редко используется для больших объёмов данных из-за своей квадратичной сложности O(n²)[1].
Критики отмечают[2], что сортировка выбором выполняет фиксированное количество операций сравнения, даже если массив частично отсортирован, что делает её менее эффективной по сравнению с адаптивными алгоритмами, такими как сортировка вставками. Кроме того, алгоритм требует много обменов элементов местами, что может быть затратно для структур данных с высокой стоимостью переназначения, например, для объектов большого размера. Тем не менее, её стабильность и предсказуемость делают её подходящей для некоторых специфических задач.
См. также
Примечания
- ↑ Перейти обратно: 1,0 1,1 1,2 1,3 Knuth, D. The Art of Computer Programming, Volume 3: Sorting and Searching. Addison-Wesley, 2nd ed., 1998.
- ↑ Перейти обратно: 2,0 2,1 2,2 2,3 Introduction to Algorithms. The MIT Press. Дата обращения: 7 февраля 2025.
