Разветвляющийся алгоритм

Программный код

Разветвля́ющийся алгори́тм — это алгоритмическая конструкция, в которой выполнение порядка действий зависит от истинности или ложности условия. Другое его название «алгоритм ветвление» или «условный алгоритм». Принцип условного исполнения алгоритма и данная алгоритмическая конструкция в программировании была изложена в 1946 году Джоном фон Нейманом. Отсюда в языки программирования стали включать команды выбора действий. Условные алгоритмы делятся на два вида: полные и неполные. Алгоритмы с полным условием имеют два блока действий, которые подразумевают выполнение соответственно при истинном и ложном результате проверки условия. Алгоритмы в неполной версии подразумевают блок действий только при истинном исходе выполнения условия.

Способы записи разветвляющегося алгоритма

Словесный способ

Способ, в котором каждый шаг алгоритма представлен в произвольном изложении на естественном языке. Данным способом передают суть алгоритма исполнителю. Такие алгоритмы могут допускать неоднозначность толкования отдельных шагов, что может привести к неправильным результатам. Пример разветвляющегося алгоритма: определить, является ли число p положительным или отрицательным. Словесный способ записи алгоритма в полной версии:

1. Начало алгоритма.
2. Ввести значение числа p.
3. Если p больше нуля, то вывести сообщение «число положительное», иначе вывести сообщение «число отрицательное».
4. Конец алгоритма.

Словесный способ записи алгоритма в неполной версии:

1. Начало алгоритма.
2. Ввести значение числа p.
3. Если p больше нуля, вывести сообщение «число положительное».
4. Если p меньше нуля, вывести сообщение «число отрицательное».
5. Если p равно нулю, вывести сообщение «число ни положительное, ни отрицательное».
6. Конец алгоритма.

Графический способ

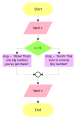
Для наглядного представления алгоритма используется графический способ. Одним из самых распространенных вариантов и часто используемых является блок-схема. Суть представления алгоритма с помощью блок-схем заключается в том, что каждый шаг алгоритма представляет собой геометрическую фигуру (блочный символ), условно обозначающий шаг алгоритма, который записывается внутри блока. Блок-схема алгоритма «ветвление» обычно состоит из блока начала/конца, блока ввода/вывода, блока выбора действий и блока действий.

• 

  Блок начала/конца алгоритма

• 

  Блок ввода/вывода

• 

  Блок действий

• 

  Блок выбора действий

• 

  Пример блок схемы разветвляющегося алгоритма

Программный способ

Он представляет собой запись алгоритма на формальном языке, а именно на языке программирования, позволяющем на основе строго определённых правил (синтаксиса, семантики и т.д.) формировать последовательность команд, однозначно отражающих смысл и содержание алгоритма для последующего выполнения его на компьютере. Программный способ подразумевает написание компьютерной программы.

Пример компьютерной программы на языке программирования Pascal: определить, является ли число p положительным или отрицательным. Программный способ записи алгоритма в полной версии:

program primer1;

var p: integer;

begin

read(p);

if p > 0 then write('число положительное')

else write('число отрицательное');

end.

Программный способ записи алгоритма в неполной версии:

program primer1;

var p: integer;

begin

read(p);

if p > 0 then write('число положительное');

if p < 0 then write('число отрицательное');

if p = 0 then write('число ни положительное ни отрицательное');

end.

Пример компьютерной программы на языке программирования Python: определить, является ли число p положительным или отрицательным:

n = int(input("Введите число: ")

if (n > 0):

    print("Число положительное")

else:

    print("Число отрицательное")

Литература

1. Кнут Дональд Эрвин. Искусство программирования. Том 1. Основные алгоритмы. — Вильямс, 2020. — 720 с. — ISBN 978-5-907144-23-1.
2. Стивен С.Скиена. Алгоритмы. Руководство по разработке. — БХВ. — 878 с. — ISBN 9785977567992.
3. Вирт Никлаус. Алгоритмы и структуры данных / с англ. Ф. В. Ткачев. — ДМК Пресс, 2013. — 272 с. — ISBN 978-5-97060-230-0.