Пирамида (геометрия)

Пятиугольная пирамида

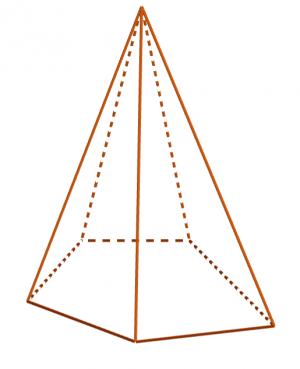
Пирамидой называется многогранник, который состоит из плоского многоугольника — основания пирамиды, точки, не лежащей в плоскости основания, — вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Пирамиды бывают треугольные, четырёхугольные и т. д., в зависимости от того, что является основанием — треугольник, четырёхугольник и т. д. Пирамида называется n-угольной, если её основанием является n - угольник. Она имеет n боковых граней.

История возникновения пирамиды

Древнегреческий математик Евклид в своих «Началах» дал первое определение пирамиды «Пирамида есть телесная фигура, заключённая между плоскостями (и) восстановленная от одной плоскости к одной точке» (книга XI, определение 12). В XII томе систематизировал знания о пирамиде. Первым греческим математиком, который установил, чему равен объём пирамиды, был Демокрит. По свидетельствам Архимеда, Демокрит установил, что пирамида равновелика 1/3 призмы, имеющей с ней одинаковые основания и высоту, но доказательств не дал. Доказательства были даны Евдоксом Книдским.

Элементы пирамиды

• Файл:Апофема пирамиды.TIFвершина пирамиды — общая точка боковых граней, не лежащая в плоскости основания;
• основание — грань, которой не принадлежит вершина пирамиды;
• боковые грани — треугольные грани, сходящиеся в вершине;
• боковые рёбра —отрезки, соединяющие вершину пирамиды с вершинами основания;
• высота пирамиды — перпендикуляр, опущенный из вершины пирамиды на плоскость её основания;
• диагональное сечение пирамиды — плоскость, проведённая через вершину пирамиды и через какую-нибудь диагональ основания.

Свойства пирамиды

Если все боковые рёбра пирамиды равны между собой, то:

• высота пирамиды проходит через центр окружности, описанной около основания;
• все боковые рёбра пирамиды составляют равные углы с плоскостью основания.

Если боковые грани пирамиды наклонены к плоскости основания под одним углом (двугранные углы при основании пирамиды равны), то

• высота пирамиды проходит через центр окружности, вписанной в основание пирамиды;
• высоты всех боковых граней, проведённые из вершины пирамиды равны.

Особые случаи пирамиды

Правильная пирамида

Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты проходит через центр этого многоугольника. В правильной пирамиде боковые рёбра равны между собой. Все боковые грани правильной пирамиды — равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.

Правильный тетраэдр

Тетраэдр

Тетраэдр — это треугольная пирамида. Правильный тетраэдр — это тетраэдр. у которого все рёбра равны. Правильный тетраэдр не имеет центра симметрии. Он имеет три оси симметрии и шесть плоскостей симметрии. Правильный тетраэдр состоит из четырёх равносторонних треугольников.

Усечённая пирамида

Пересечём пирамиду плоскостью, параллельной основанию. получим две части: пирамиду, подобную данной и усечённую пирамиду. Многоугольник, полученный от пересечения пирамиды и секущей плоскости, называется верхним основанием, а основание исходной пирамиды есть основание получившейся усечённой пирамиды. Расстояние между секущей плоскостью и нижним основанием, называется высотой усечённой пирамиды.

Основные формулы

Формула для вычисления объёма пирамиды: V=${\frac {1}{3}}$S$\centerdot$h, где S — площадь основания, h — высота пирамиды.

Площадью полной поверхности пирамиды называется сумма площадей всех её граней (основания и боковых граней) Sполн=Sбок+Sосн.

Площадь боковой поверхности пирамиды называется сумма площадей всех её боковых граней.

Площадь боковой поверхности правильной пирамиды равна: Sбок=${\tfrac {1}{2}}$Ра, где Р — периметр основания, а — апофема.

Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.

Теоремы, связывающие пирамиду с другими геометрическими телами

Шар, сфера

Тетраэдр, вписанный в шар

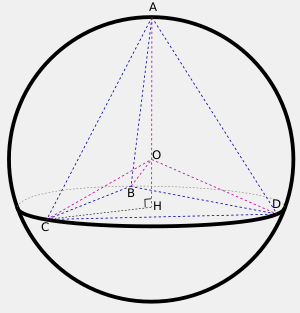
Около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность. Центр шара, описанного около правильной пирамиды лежит на её оси.

Конус

Пирамидой, вписанной в конус, называется такая пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершина является вершиной конуса. Боковые рёбра пирамиды, вписанной в конус, являются образующими конуса. Если все боковые рёбра пирамиды равны, то она вписана в конус. Пирамидой, описанной около конуса, называется пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.

Цилиндр

Пирамида называется вписанной в цилиндр, если ее вершина принадлежит одному основанию цилиндра, а основание вписано в другое основание цилиндра. В цилиндр можно вписать пирамиду, если основание пирамиды можно вписать в окружность. Высота вписанной пирамиды равна высоте цилиндра. Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью, вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды. В сечении пирамиды плоскостью, параллельной основанию, получается многоугольник, подобный основанию пирамиды. В пирамиду можно вписать цилиндр только в том случае, если в основании пирамиды — многоугольник, в который можно вписать окружность.

Примечание

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!