Гипотеза Пуанкаре

Гипо́теза Пуанкаре́ — доказанная математическая гипотеза о том, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере. Сформулированная в 1904 году математиком Анри Пуанкаре гипотеза была доказана в серии статей 2002—2003 годов Григорием Перельманом. После подтверждения доказательства математическим сообществом в 2006 году гипотеза Пуанкаре стала первой и единственной на данный момент (2024 год) решённой задачей тысячелетия.

Гипотеза является результатом четырёхмерной сферы (3-сфера). Гипотеза перестала быть гипотезой и превратилась в теорему после её математического доказательства в 2006 году, математиком Григорием Перельман. Теорема утверждает, что четырёхмерная сфера, также называемая 3-сферой или гиперсферой, является единственным компактным четырёхмерным многообразием, в котором каждая петля или замкнутый круг (1-сфера) могут быть деформированы (преобразованы) в точку. Последнее утверждение эквивалентно утверждению, что существует только замкнутое и односвязное многообразие размерности 3: четырёхмерная сфера.

История возникновения

Изображение сфер

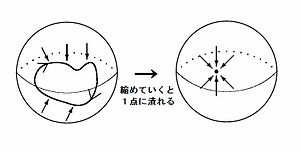
Поверхность футбольного мяча, например, является почти примером 2-мерного многообразия, 2-сферы. Человек может манипулировать им как угодно, придавая ему разные формы, но не разрушая его, и он останется 2-сферой. Критерий проверки того прост: представьте себе чрезвычайно деформируемую резиновую ленту, лежащую на поверхности воздушного шара; если резину можно сжать (не отрываясь от поверхности), пока она не займёт одну точку, и это в любом месте на поверхности, то воздушный шар является однородным. 2-сфера и называется просто связанной.

Проблема классификации многообразий в пространстве с использованием в качестве критерия классификации концепции гомеоморфизма была решена в XIX веке. Сфера представляет собой многообразие размерности 2 (каждый маленький кусочек сферы представляет собой небольшой кусочек слегка деформированной плоскости), замкнутое и односвязное, и было установлено, что каждое многообразие размерности 2, замкнутое и односвязное гомеоморфно сфере. Иными словами: существует только одно (гомеоморфное) многообразие размерности n = 2, замкнутое и односвязное, и это сфера (и её гомеоморфы).

В 1904 году французский математик Анри Пуанкаре (1854 год — 1912 год) предположил, что результат, полученный для сферы n= 2 3-мерного пространства, имеет аналог для сферы n= 3 4-мерного пространства. Другими словами, в 4-мерном пространстве всё многообразие размерностей имеет аналог. n=3, замкнутое и односвязное, было бы гомеоморфно сфере размерности n = 3. Но Пуанкаре не удалось доказать свою гипотезу. Как и никто из его современников или преемников. Со временем гипотеза Пуанкаре приобрела интерес, пока не стала самой заметной открытой проблемой геометрической топологии с заметными последствиями для физики. Более того, она стала одной из самых важных нерешённых проблем математики.

Для второго измерения это было доказано ещё в XIX веке. Для n = 5 пришлось подождать до 1961 года, когда это сделал Эрик Кристофер Зееман. В том же году Стивен Смейл получил его для n, равного или большего 7, а в 1962 году Джон Р. Столлингс для случая n = 6. Случаи n = 3 и n = 4 сопротивлялись, и пришлось ждать 1986 года, когда американцу Майклу Хартли Фридману удалось доказать случай n = 4. Проблема в том, что исходный случай n = 3, успешно разрешённый для всех других измерений, выдвинутый Пуанкаре, категорически сопротивлялся любому математическому доказательству, пока русский математик Григорий Перельман не обнародовал свой подвиг, опубликовав своё доказательство. Анри Пуанкаре выдвинул такую гипотезу в 1904 году, заявив, что трёхмерная сфера уникальна и что ни одна из других трёхмерных разновидностей не обладает её свойствами.

Разрешение гипотезы

Григорий Перельман разрешил гипотезу Пуанкаре. Именно за решение этой проблемы Перельман был награждён в 2006 году медалью Филдса, считающейся Нобелевской премией по математике, ещё одной наградой, от которой он также отказался. Гипотеза Пуанкаре до того, как она была доказана, была одним из важнейших открытых вопросов топологии. В 2000 году она была названа одной из семи задач тысячелетия, за решение которых Институт математики Клея предложил приз в размере 1 миллиона долларов за первое правильное решение. Работа Перельмана выдержала проверку и была подтверждена в 2006 году, за что ему была предложена медаль Филдса, от которой он отказался.

18 марта 2010 года Перельман был удостоен премии Тысячелетия. 1 июля 2010 года он отказался от награды, заявив, что считает свой вклад в доказательство гипотезы Пуанкаре не большим, чем гипотеза Гамильтона. Гипотеза Пуанкаре — единственная решённая проблема тысячелетия.

Перельман доказал гипотезу, деформировав многообразие потоком Риччи (который ведёт себя аналогично уравнению теплоты, описывающему диффузию тепла через объект). Поток Риччи обычно деформирует многообразие в сторону более округлой формы, за исключением некоторых случаев, когда он растягивает многообразие, отделяя его от самого себя, в направлении так называемых особенностей. Затем Перельман и Гамильтон разрезают многообразие на сингулярности (процесс, называемый «хирургией»), в результате чего отдельные части приобретают сферическую форму. Основные этапы демонстрации состоят в том, чтобы показать, как ведут себя многообразия при деформации потоком Риччи, изучить, какие особенности развиваются, определить, можно ли завершить этот процесс операции, и установить, что операцию не нужно повторять бесконечно много раз.

Первый шаг — деформировать многообразие с помощью потока Риччи. Поток Риччи был определён Ричардом Стрейтом Гамильтоном как способ деформации многообразий. Формула потока Риччи представляет собой имитацию уравнения теплоты, которое описывает способ, которым тепло течёт в твёрдом теле. Как и тепловой поток, поток Риччи имеет тенденцию к равномерному поведению. В отличие от теплового потока, поток Риччи может столкнуться с особенностями и перестать функционировать. Сингулярность в многообразии — это место, где она неразличима: например, угол, выступ или выступ, щепотка. Поток Риччи был определён только для гладких и дифференцируемых многообразий. Гамильтон использовал поток Риччи, чтобы доказать, что некоторые компактные многообразия диффеоморфны сферам, и надеялся применить его для доказательства гипотезы Пуанкаре.

Гамильтон составил список возможных особенностей, которые могут быть сформированы. Он хотел разрезать многообразие на сингулярности и приклеить колпачки, а затем снова запустить поток Риччи, поэтому нужно было понять особенности и доказать, что определённые типы особенностей не встречаются. Перельман обнаружил, что все особенности очень просты: по сути, трёхмерные цилиндры, образованные сферами, вытянутыми вдоль линии. Обычный цилиндр изготавливается путём взятия кругов, вытянутых вдоль линии. Перельман доказал это, используя нечто, называемое «уменьшенный объём», которое тесно связано с собственным значением определённого эллиптического уравнения.

Иногда сложная операция сводится к умножению на скаляр (число). Такие числа называются собственными значениями этой операции. Собственные значения тесно связаны с частотами колебаний и используются при анализе известной проблемы: слышите ли вы звук барабана? По сути, собственное значение похоже на ноту, играющую на многообразии. Перельман показал, что эта нота возрастает по мере деформации многообразия потоком Риччи. Это помогло ему устранить некоторые из наиболее проблемных особенностей, которые беспокоили Гамильтона, в частности решение сигарообразного солитона, который выглядел как нить, торчащая из многообразия, с другой стороны которой ничего нет. По сути, Перельман доказал, что все образующиеся нити можно разрезать и заделать, и что ни одна из них не выступает только с одной стороны.

Чтобы завершить доказательство, Перельман берёт любое компактное, односвязное и неограниченное трёхмерное многообразие и начинает выполнять поток Риччи. Это деформирует сорт на круглые кусочки, между которыми проходят нити. Он обрезает нити и продолжает деформировать сорт, пока в итоге не останется набор трёхмерных круглых сфер. Затем он реконструирует исходное многообразие, соединяя сферы друг с другом с помощью трёхмерных цилиндров, преобразует их в круглую форму и проверяет, что, несмотря на всю первоначальную путаницу, многообразие действительно было гомеоморфно сфере.

Сразу же возник вопрос, как можно быть уверенным в том, что бесконечные сокращения не нужны. Это было высказано на том основании, что сокращение может продолжаться вечно. Перельман показал, что этого не может быть при использовании минимальных поверхностей в многообразии. Минимальная площадь поверхности — это, по сути, мыльная плёнка. Гамильтон показал, что площадь минимальной поверхности уменьшается по мере того, как многообразие испытывает поток Риччи. Перельман проверил, что происходит с минимальной площадью поверхности при нарезке сорта. Он доказал, что в конечном итоге площадь настолько мала, что любой разрез после того, как площадь станет такой маленькой, может быть разрезом только трёхмерных сфер, а не более сложных деталей. Кристина Сормани описывает это как битву с гидрой в цитируемой ниже книге Шпиро . Эта последняя часть доказательства появилась в третьей и последней статье Перельмана на эту тему.

Демонстрация гипотезы

В обычной сфере-2 любую петлю можно непрерывно затягивать, пока она не станет точкой на поверхности. Характеризует ли это условие сферу-2? Ответ — да, и он давно известен. Гипотеза Пуанкаре задаёт тот же вопрос для сферы-3, которую невозможно визуализировать. Григорий Перельман доказал истинность этой гипотезы. Это утверждение не могло быть решено в течение столетия, и его доказательство считалось одной из семи задач тысячелетия, предложенных Математическим институтом Клэя. Российский математик Григорий Перельман объявил об этом в 2002 году в двух публикациях в Интернете.

5 июня 2006 года китайские математики Чжу Сипин и Цао Хуайдун объявили о полном доказательстве, основанном на предварительных работах Перельмана (они действительно были опубликованы в специализированных журналах), которые, после их подтверждения математическим сообществом, положат конец полной классификации структур Пуанкаре. Однако большая часть математического сообщества считает, что доказательство принадлежит Перельману, и считает работу китайских математиков плагиатом. Китайская академия наук в защиту Чжу Сипина и Цао Хуайдуна заявила, что русский «изложил общие положения для проверки гипотезы, но не сказал конкретно, как решить загадку».

17 мая 2011 года работа Перельмана была признана, когда он был награждён премией Филдса в рамках XXV Международного конгресса математиков, базирующийся в Мадриде. В августе 2006 года Перельман не явился на Мадридский конгресс и отказался от премии. Он не даёт интервью, за исключением, например, американского еженедельника (The New Yorker), где он утверждал, что не хочет быть «талисманом» в мире математики, полагая, что ему не нужно никакого другого признания, кроме достоверности его работы.

Поток Риччи с операцией

Программа Гамильтона для доказательства гипотезы Пуанкаре состоит в том, чтобы сначала поместить риманову метрику в неизвестное односвязное замкнутое третье многообразие. Основная идея состоит в том, чтобы попытаться «улучшить» эту метрику; например, если метрику можно улучшить настолько, чтобы она имела постоянную положительную кривизну, то, согласно классическим результатам римановой геометрии, она должна быть 3-сфера. Гамильтон прописал «уравнения потока Риччи» для улучшения метрики;

где g — метрика, а R — её кривизна Риччи, и ожидается, что с увеличением времени t многообразие будет легче понять. Поток Риччи расширяет часть многообразия с отрицательной кривизной и сжимает часть многообразия с положительной кривизной.

В некоторых случаях Гамильтону удалось доказать, что это работает; например, его первоначальный прорыв заключался в доказательстве того, что если риманово многообразие имеет положительную кривизну Риччи везде, то описанная выше процедура может выполняться только для ограниченного интервала значений параметров, причём, что более важно, что существуют такие числа, что в качестве риманова метрика плавно сходится к метрике постоянной положительной кривизны. Согласно классической римановой геометрии, единственное односвязное компактное многообразие, которое может поддерживать риманову метрику постоянной положительной кривизны, — это сфера. Таким образом, действительно, Гамильтон доказал частный случай гипотезы Пуанкаре: если односвязное компактное 3-кратное допускает положительную риманову метрику кривизны Риччи, то она должна быть диффеоморфна 3-сфера.

С другой стороны, имеется только одна произвольная риманова метрика, уравнения потока Риччи должны привести к более сложным особенностям. Величайшим достижением Перельмана было доказать, что, если принять определённую перспективу, если они появляются за конечное время, эти особенности могут выглядеть только как сжимающиеся сферы или цилиндры. Обладая количественным пониманием этого явления, он разрезал многообразие по сингулярностям, разделив многообразие на несколько частей, а затем продолжил поток Риччи на каждой из этих частей. Эта процедура известна как поток Риччи с хирургическим вмешательством.

Перельман представил независимый аргумент, основанный на сокращении потока кривых, чтобы доказать, что в односвязном компактном 3-многообразии любое решение потока Риччи с помощью операции затухает за конечное время. Альтернативный аргумент, основанный на минимально-максимальной теории минимальных поверхностей и геометрической теории мер, был предложен Тобиасом Колдингом и Уильямом Миникоцци. Таким образом, в односвязном контексте вышеупомянутое конечно временное явление потока Риччи с хирургическим вмешательством — это все, что имеет отношение к делу. Фактически, это верно, даже если фундаментальная группа является свободным произведением конечных групп и циклических групп.

Это условие о фундаментальной группе оказывается необходимым и достаточным для исчезновения за конечное время. Это равносильно утверждению, что простое разложение многообразия не имеет ациклических компонентов, и оказывается эквивалентным условию, что все геометрические фигуры в многообразии имеют геометрию, основанную на двух геометриях Терстона S2× R и S³. В контексте, в котором не делается никаких предположений о фундаментальной группе Перельман провёл дальнейшее техническое исследование предела многообразия для бесконечно больших времён и тем самым доказал гипотезу Терстона о геометризации: в большие времена многообразие имеет «грубое-тонкое разложение», толстая часть которого имеет гиперболическую структуру, а тонкая часть — графическое многообразие. Однако из-за результатов Перельмана, Колдинга и Миникоцци эти дополнительные результаты не нужны для доказательства гипотезы Пуанкаре.

В культуре

Максим Темп описал простыми словами гипотезу на сайте Проза.ру. Сказку о математике Григории Перельмане, который решил одну из семи задач тысячелетия написал Ник Горькавый, напечатанный в журнале «Наука и жизнь» в номере № 8 в 2018 году.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!