Участник:Markoveug BZ 49/Черновик
Шаблоны (subst:L) и (карточка прибора)
Эта страница - правильный черновик
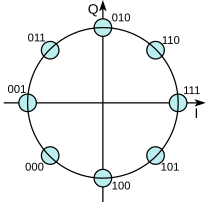
Код Гре́я (англ. Gray code ) — двоичный код, использующий символы 0 и 1, в котором две соседние кодовые комбинации различаются между собой значением символа только в одном разряде (одношаговый код). Иными словами, расстояние Хэмминга — мера различия между соседними кодовыми комбинациями — равно единице.
Строго говоря, существует множество кодов Грея для систем счисления с любым основанием и в общем виде можно записать представление этого множества как {Gray (n,k)}, где
n - основание системы счисления,
k - число цифр в коде.
Однако в большинстве случаев под термином «код Грея» понимают именно бинарный код, в котором n = 2. В этом случае, поскольку основание системы является чётным числом, код имеет «зеркальную» циклическую структуру, то есть является рефлексивным (от лат. reflexio — обращение назад, отражение)[1].
История изобретения
Код назван в честь исследователя Фрэнка Грея, работавшего в лаборатории «Bell labs». В 1947 году была подана заявка на патент под названием «импульсный код связи», которая была удовлетворена в 1953 году (патент № 2632058)[2]. Код назван «рефлексивным» (отражённым) из-за того, что первая половина значений при изменении порядка эквивалентна второй половине, за исключением старшего бита. Старший бит просто инвертируется. При делении каждой новой половины пополам это свойство сохраняется.
Отраженный двоичный код применялся для решения математических задач, а затем получил использование в технике, в частности, для защиты от ложного прочтения состояния электромеханических и электронных переключателей, когда необходимо исключить логические гонки. Французский инженер Эмиль Бодо применил код Грея в 1878 году в телеграфии, за эту работу он был награжден орденом Почётного легиона.
В настоящее время код Грея используется при составлении алгоритмов для создания карт Карно, которые, в свою очередь, используются в качестве инженерного инструмента при проектировании комбинационных и последовательностных логических схем. Кроме того, код Грея применяется для упрощения выявления и исправления ошибок в системах связи, а также для формирования последовательности импульсов в линейных и круговых датчиках отсчёта — энкодерах[3].
Преимущества кода Грея
Характерной особенностью кода Грея является изменение только одной позиции при переходе от одного кодовой комбинации к другой. Это свойство широко используют как для построения некоторых типов АЦП, где он позволяет свести к «единице» младшего разряда погрешность неоднозначности при считывании, так и для решения других задач, требующих минимизировать погрешность перехода.
Если при преобразовании линейных и угловых перемещений использовать обычный двоичный код без дополнительного синхроимпульса, то расположенные рядом кодовые комбинации могут различаться одновременно в нескольких разрядах, поскольку двоичный код является многошаговым. Например, если на границе перехода возникла совокупность комбинаций 0111 и 1000, различающихся во всех разрядах, то за счёт неточности изготовления или установки считывателя, или неодновременности срабатывания ключей может быть прочитана ложная комбинация «нулей» и «единиц». Допустим, что третий справа считыватель сработал с отставанием, тогда в какой-то момент вместо комбинации 1000 будет прочитана комбинация 1100. Применение кода Грея для решения подобных задач позволяет свести ошибки к минимуму.
Представление информации в коде Грея
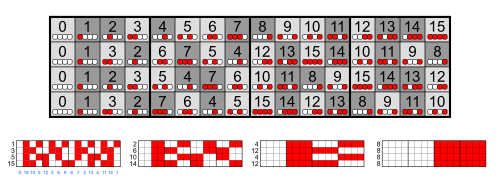
Ниже на иллюстрации приведены несколько вариантов генерации кода Грея путём изменения соседних 4-битных последовательностей таким образом, что при переходе позиции меняется только один бит.
Алгоритм построения кода Грея
Для перевода неотрицательного двоичного числа А2 в код Грея необходимо выполнение следующих правил:
- единица в старшем разряде сохраняется;
- значения каждого из младших разрядов кода Грея (gi) определяется сравнением значений текущего (bi) и старшего (bi+1) разрядов двоичного числа. Если значения совпадают, в разряд gi записывается ноль, если различаются — единица.
Ниже приведена таблица представления чисел в двоичном коде и в коде Грея
| А2 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Код Грея | 0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
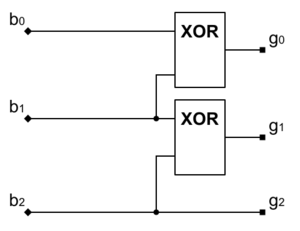
Конвертор двоичных чисел в код Грея можно реализовать на логических элементах "Исключающее ИЛИ" (полусумматор):
Преобразование кода Грея в двоичное число
Для перевода кода Грея в двоичное число необходимо выполнение следующих правил:
- единица в старшем разряде сохраняется;
- если разряд i кода Грея содержит 0, то в разряд i двоичного числа записывается значение i−1 разряда двоичного числа;
- если разряд i кода Грея содержит 1, то в разряд i двоичного числа записывается инвертированное значение i − 1 разряда двоичного числа.
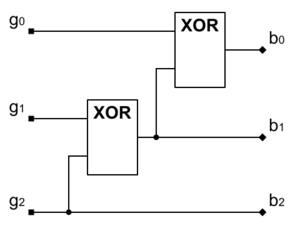
Поскольку информация, выраженная в виде кода Грея, не несёт реальной числовой информации, перед дальнейшей обработкой её необходимо преобразовать в стандартный бинарный код — двоичное число. Конвертор из кода Грея в двоичное число также можно реализовать на логических элементах "Исключающее ИЛИ":
Примечания
- ↑ КОД ГРЕЯ. Сайт phg.su. Дата обращения: 11 апреля 2024.
- ↑ Pulse code communication (англ.). Unite States Patent and Trademark offise (17 марта 1953). Дата обращения: 12 апреля 2024.
- ↑ Н. И. Сорока, Г. А. Кривинченко. Коды и кодирование. Конспект лекций. Министерство образования Республики Беларусь. Дата обращения: 11 апреля 2024.
Ссылки
Системное программирование. Обработка данных в форматах ASCII и BCD