Триангуляция

Карта триангуляции

Триангуля́ция (от лат. triangulum — треугольник) — метод определения плановых координат геодезических пунктов, основанный на построении треугольных цепей и сетей на местности. Геодезические пункты размещаются в вершинах треугольников, к которым прилегают геодезические знаки с визирными цилиндрами, для наведения угломерных инструментов с соседних пунктов.

История

Триангуляция XVI века

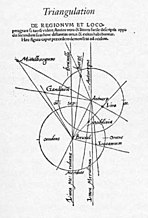
Снеллиус Снель ван Ройен (1580—1626) основоположник первых градусных измерений в геодезических сетях. Им впервые выполнены градусные измерения с использованием метода триангуляции.

Работы по созданию первой обширной триангуляционной сети в России начались в Санкт-Петербурге в сентябре 1809 года. Это стало отправной точкой для создания более точной астрономо-геодезической основы для топографических измерений. Руководил этими работами Карл Иванович Теннер, известный учёный и будущий выдающийся геодезист и астроном. Для измерения углов использовались различные инструменты, включая повторительный круг Траутона и теодолит Рамсдена. Там, где использование теодолита было невозможно, углы измерялись с помощью секстанта.

Источники ошибок

Основные проблемы использования метода триангуляции в практических задачах связаны с необходимостью оценки координат большого количества объектов, видимых из разных точек наблюдения. Ограничение количества точек наблюдения до двух или трёх не рекомендуется, так как это может привести к потере информации и затруднить достижение цели — упрощения процесса определения истинных координат объектов. Если каждый объект имеет несколько линий положения, он идентифицируется по наиболее подходящей линии, соответствующей заданному критерию. Типичная ситуация — когда каждому объекту на каждой точке наблюдения соответствует только один признак — одна линия положения. Эта задача актуальна при наблюдении радиоконтрастных объектов под малыми углами в сетях связи. Базовая суть задачи сохраняется, если предположить, что на каждой точке наблюдения измеряется направление на объекты, находящиеся на одной плоскости, и их линии положения. Для однозначного решения задачи, если число объектов для локализации превышает один, требуется как минимум три пеленга на каждый объект.

Способы измерения углов

Способ Шрейбера

С 1908 года в угловых измерениях начали применять способ Шрейбера. Сначала его использовали в дополнительном классе военно-топографического училища на летней практике. Затем, с 1909 года, под руководством полковника Павлова, этот способ стали применять при измерении углов в триангуляции 1 класса в Омском топографическом отделе. В 1910 году под руководством Померанцева была разработана инструкция для триангуляции 1 класса, где рекомендовалось использовать способ Шрейбера. Несмотря на ограничения инструментов, Теннер и Струве достигли в угловых измерениях высокой точности. Теннер показывал ошибки измеренных углов порядка 0°70'×0°98' при использовании метода повторений.

Способ Струве

Метод круговых приемов — метод Струве. Данный метод был предложен в 1816 году Струве и нашёл широкое применение почти во всех странах. В России он используется в геодезических сетях 2-4 классов и сетях более низкой точности. При использовании этого метода при неподвижном лимбе алидаду вращают по ходу часовой стрелки, а биссектор сетки нитей трубы последовательно наводят на первый, второй,…, последний и снова на первый (замыкание горизонта) наблюдаемые пункты, отсчитывая каждый раз по горизонтальному кругу. Это первый полуприём. Затем трубу переводят через зенит и, вращая алидаду против часовой стрелки, наводят биссектор на те же пункты, но в обратной последовательности: на первый, последний, …, второй, первый; завершается второй полуприём и первый приём, состоящий из первого и второго полуприёмов.

Способ неполных приёмов

Триангуляция Герлинга Курхессена, 1837 год

Метод неполных приёмов был предложен Аладжаловым в 1954 году. Он заключается в разбиении всех направлений на группы из трёх направлений без замыкания горизонта. Это позволяет уменьшить объём работы и увеличить количество прямых измерений каждой группы направлений. Таким образом, этот метод стремится устранить недостатки методов Струве и Шрейбера при наблюдении на пунктах с большим количеством направлений. Иногда не удается разбить направления на группы из трёх направлений, и в этом случае измеряются отдельные углы, дополняющие программу.

Классы и разряды

Триангуляция 1 класса представляет собой астрономо-геодезическую сеть 1 класса, которая совместно с гравиметрической съёмкой помогает решить научные задачи по определению формы и размеров Земли, а также изучению движений и деформаций земной коры. Она также служит основой для развития геодезических сетей более низких классов и целью имеет распространение единой системы координат на всю территорию России. Сеть 1 класса построена с высочайшей точностью, использовавшейся в современном приборостроении, и с применением тщательно продуманной методики измерений. Сеть состоит из полигонов, каждый из которых не превышает 200 км, при периметре полигона порядка 800—1000 км.

Триангуляция 2 класса строится как сплошная сеть треугольников, заполняющих полигоны триангуляции 1 класса. Она является опорной сетью, служащей для развития более детальных сетей и геодезического обоснования топографических съёмок и инженерных изысканий. Сеть 2 класса также может использоваться для научных исследований благодаря своей жёсткости и высокой точности. Триангуляция 3 и 4 классов представляет собой дальнейшее сгущение государственной геодезической сети для крупномасштабного картографирования и обоснования строительства инженерных сооружений.

Триангуляция 1 и 2 разряда применяется для увеличения плотности геодезических сетей на местности, обеспечивая необходимую точность для проведения крупномасштабных съёмок, особенно в открытых или гористых районах, а также в случаях, когда полигонометрия неэффективна или невозможна. Исходными точками для развёртывания триангуляции 1 разряда служат точки государственной геодезической сети 1 — 4 классов, а для триангуляции 2 разряда — точки государственной геодезической сети и точки триангуляции и полигонометрии 1 разряда. В зависимости от расположения и плотности исходных точек на местности, триангуляция 1 разряда формируется в виде сетей, цепей треугольников и добавления отдельных точек в уже существующие треугольники, образованные точками сетей 2 — 4 классов. Триангуляция 2 разряда развивается в виде сетей, отдельных точек или групп точек между точками сетей 2 — 4 классов, а также 1 разряда.

Базисная сеть

Трехмерная триангуляция. Схема Джеммы Фризиус, 1533 год

Базисные сети используются в основном для плавного перехода от короткого базиса к более длинной стороне тригонометрической сети. Установлено, что для этого необходимо расположить базис и сторону так, чтобы базис представлял собой малую диагональ, а сторона — большую диагональ ромба, вершинами которого являются две точки стороны и два конца базиса. Для этого базис помещают посередине стороны, приблизительно перпендикулярно к ней, и делают размеры базиса примерно в 4—5 раз меньше длины стороны.

Основные ряды триангуляции второго класса или астрономо-геодезическая сеть второго класса разбивает каждый полигон триангуляции первого класса на шесть частей путём проложения в нём основных и независимых рядов триангуляции второго класса, опирающихся на точки Лапласа. Ряды рассматривались как звенья, которые можно уравнивать отдельно, что упрощает уравнивание сети второго класса. В пересечении основных рядов триангуляции второго класса строится базисная сеть, из которой определяется длина выходной стороны.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!