Релейно-контактные схемы, программное представление

Релейно-контактные схемы (РКС) — это электрические схемы, состоящие из проводников и двухпозиционных контактов, через которые источник тока связан с потребителями. Контакты подразделяются на замыкающие и размыкающие. В качестве потребителей могут выступать как конечные (исполнительные) элементы схемы, так и промежуточные. Схема создаётся из отдельных деталей, соединяемых между собой посредством проводного (аппаратного) монтажа.

Функциональными аналогами аппаратных релейно-контактных схем являются программы, выполненные на графическом языке программирования логического контроллера (ПЛК), реализующем структуры электрических цепей. При этом в качестве промежуточных элементов схемы используются внутренние битовые переменные, а исполнительные элементы, подключенные к выходам ПЛК, реализованы аппаратно. В соответствии с заложенным алгоритмом программа решает, какие выходы активировать или деактивировать в зависимости от состояния входных сигналов и промежуточных переменных.

Элементы релейно-контактных схем

Пример релейно-контактной схемы в соответствии с ГОСТ 2.755—87 ЕСКД

Элементы, из которых состоит аппаратная релейно-контактная схема, можно разделить по их назначению на несколько групп:

• Элементы, воспринимающие воздействия извне и в соответствии с ними производящие замыкание или размыкание отдельных цепей схемы. Таковы контакты ручных или автоматических переключателей (кнопки, переключатели, контактные группы датчиков). Эти элементы называются внешними или приёмными.
• Другие элементы являются внутренними составляющими релейно-контактной схемы, они реагируют на замыкание или размыкание её цепей. Эти элементы по их назначению в свою очередь можно разделить на исполнительные и промежуточные.

Исполнительные элементы непосредственно производят коммутацию силовых цепей и приводят в действие исполнительные механизмы. Это контакторы электродвигателей или катушки гидравлических или пневматических клапанов. Промежуточные элементы являются частью схемной реализации алгоритма управления и служат для выработки управляющих сигналов, участвующих в формировании соответствующих условий для работы исполнительных элементов.

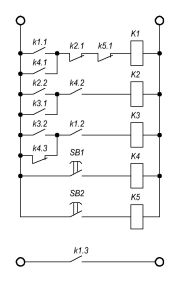
На иллюстрации приведён пример релейно-контактной схемы, элементы которой изображены в соответствии с требованиями ГОСТ 2.755—87 ЕСКД (Единая система конструкторской документации).

Устройство электромеханического реле

• 
• 

Устройство электромеханического реле и его схемное обозначение

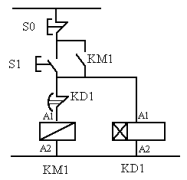
Внешний вид электромеханического реле

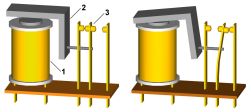
Одним из основных элементов релейно-контактной схемы является электромеханическое реле. На иллюстрациях показаны внешний вид, принцип работы электромеханического реле и схемное обозначение катушки реле и связанной с ним переключающей контактной группы.

В соответствии с принятой терминологией названия контактов соответствуют их положению при отсутствии напряжения на выводах А1-А2, а именно: замыкающие контакты реле называются нормально разомкнутыми (группа 11-14), а размыкающие — нормально замкнутыми (группа 11-12).

Когда катушка реле (1) находится под напряжением, сердечник притягивает подвижный якорь (2), в результате работы переключающей контактной группы (3) нормально разомкнутые контакты замыкаются, а нормально замкнутые — размыкаются.

В исходное положение якорь возвращается пружиной.

Релейно-контактные схемы и логические функции

В 1938 году американский инженер и учёный, основатель математической теории информации Клод Шеннон опубликовал статью «Символический анализ релейных и переключательных цепей» (англ. A symbolic analysis of relay and switching circuits), в которой было показано применение аппарата математической логики и булевой алгебры для анализа и синтеза релейно-контактных переключательных схем. Шеннон показал, как используя математический аппарат логических отношений, можно построить электрические цепи.

Свои идеи относительно связи между двоичным исчислением, булевой алгеброй и электрическими схемами Шеннон развил в докторской диссертации, опубликованной в том же 1938 году.

Примерно в то же время (в 1938 - 1941 г.г.) аналогичную по тематике и значимости работу провёл и советский учёный Виктор Шестаков, специализировавшийся в области математической логики и теории электротехники .

В этой концепции каждому контакту схемы сопоставлялся логический «0», если контакт был разомкнут, и логическая «1», если контакт был замкнут. Таким образом множеству переменных булевой алгебры {0,1} сопоставлялось множество физических состояний {«контакт разомкнут», «контакт замкнут»}.

Пример программной реализации релейно-контактной схемы с использованием символов ГОСТ МЭК 61131-1-2016

В настоящее время построение схем и систем управления в конструктиве аппаратной релейной логики используется редко, поэтому в дальнейшем вместо ранее приведённых обозначений элементов релейно-контактной схемы используем обозначения, введённые стандартом ГОСТ Р МЭК 61131-1-2016 для построения логических цепей путём программирования логических контроллеров (ПЛК) на языке релейных (лестничных) диаграмм — Ladder diagram (англ. LD, LAD).

В языке программирования LD используются символы, аналогичные функционально и по начертанию элементам релейной схемы. Это позволяет как разработчикам, так и обслуживающему персоналу достаточно легко перейти к созданию и прочтению логических цепей.

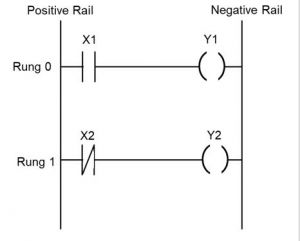
Например, на приведённой слева схеме такими символами обозначены:

• элемент Х1 — переменная, функционально аналогичная нормально разомкнутому контакту реле Х1;
• элемент Х2 — переменная, функционально аналогичная нормально замкнутому контакту реле Х2;
• элементы Y1 и Y2 — переменные, функционально аналогичные катушкам реле Y1 и Y2;

Реализация функции «И» для двух переменных

Примеры программной реализации логических цепей

Допустим, нам необходимо получить сигнал на выходе логического устройства только в случае, если на его вход будут одновременно поданы два входных сигнала.

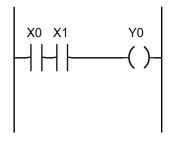
Эта описанная словесно ситуация соответствует логической операции «И» с двумя переменными. Для её технической реализации на релейно-контактных элементах необходимо обеспечить срабатывание электромагнитного реле Y0, для чего сигналы (напряжения) подаются на обмотки катушек двух реле X0, X1, соответствующие контакты которых которых включены последовательно с обмоткой реле Y0. При замыкании обоих контактов, т.е срабатывании обоих реле X0 и X1, напряжение подается на обмотку реле Y0.

Реализация функции «ИЛИ» для двух переменных

В случае реализации функции программным путём необходимо, чтобы переменные X0 и X1 одновременно приняли значения логической «1». В этом случае значение переменной Y0 будет равно логической «1».

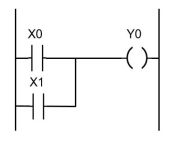
Аналогично можно реализовать логическую операцию «ИЛИ». В случае технической реализации схемы на релейно-контактных элементах для срабатывания электромагнитного реле Y0 необходимо включить контакты X0, X1 параллельно. При этом напряжение на обмотку реле Y0 будет подано при замыкании или контакта X0, или контакта X1, или обоих контактов одновременно, т.е. при срабатывании любого из реле (X0 и X1), либо при их одновременном срабатывании.

Для реализации функции «ИЛИ» программным путём необходимо, чтобы либо переменная X0, либо переменная X1, либо обе переменные одновременно имели значение логической «1».

Во всех этих случаях значение переменной Y0 также будет равно логической «1».

Сравнительные примеры аппаратной и программной реализации релейно-контактных схем

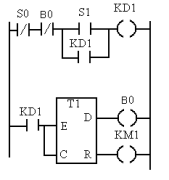
Приведём варианты релейно-контактных схем, выполненных на аппаратной основе и в виде программных логических цепей.

• 
• 

Аппаратная реализация схемы Программная реализация схемы

Из приведённых примеров видно, что если сравнивать программу с электрической схемой, значения состояний переменных соответствуют наличию или отсутствию электрического потенциала в каждом соединительном узле схемы.

Следует отметить, что программная реализация структуры электрических цепей предоставляет гораздо больше возможностей, чем аппаратная реализация.

Программная реализация реверсивного счётчика

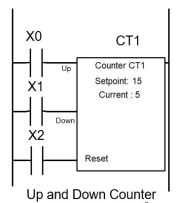
Например, программа, написанная с использованием языка LD и выполняющая функцию реверсивного счётчика, выглядит достаточно просто, поскольку в качестве собственно счётчика CT1 использован библиотечный элемент (подпрограмма), входящий в состав специализированного программного комплекса, предназначенного для программирования ПЛК.

Если переменные X0, X1, X2 имеют значение логического «0», счётчик сохраняет значение предыдущего цикла счёта; если X2 принимает значение логической «1», счётчик сбрасывается, т.е. текущее значение счёта становится равным нулю.

При подаче импульсов логической «1» на входы Up (прямой счёт), либо Down (обратный счёт) и отсутствии логической «1» на входе Reset (сброс), запускается процесс прямого или обратного счёта соответственно. На приведённой иллюстрации отражены как предустановленное значение счёта (Setpoint: 15), так и его текущее значение (Current: 5).

В то же время аппаратная реализация подобной функции потребовала бы применения отдельного специализированного электронного устройства — счётчика импульсов, стоимость которого достаточно высока. Кроме того, ресурс работы общей схемы был бы ограничен временем безотказной работы обеспечивающей релейной схемы.

Принципы минимизации

Сложность логической функции, а отсюда сложность и стоимость реализующей её релейно-контактной схемы, пропорциональны числу логических операций и числу используемых аппаратных средств. Для программной реализации количество используемых переменных не столь существенно, однако скорость выполнения, а также прочтения и понимания программы, напрямую зависят от простоты построения логических цепей.

Для минимизации переменных в логической цепи (схеме) существует математический аппарат упрощения логических выражений посредством аксиом и теорем алгебры логики.

Некоторые преобразования логических формул схожи с преобразованиями формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. д.), тогда как другие преобразования основаны на приёмах, не свойственных операциям обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, законов де Моргана и других).

Основным методом минимизации логических функций являются операции попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

${\overline {X}}_{1}X_{2}X_{3}X_{4}\vee {\overline {X}}_{1}X_{2}{\overline {X}}_{3}X_{4}={\overline {X}}_{1}X_{2}X_{4}(X_{3}\vee {\overline {X}}_{3})={\overline {X}}_{1}X_{2}X_{4}\cdot 1={\overline {X}}_{1}X_{2}X_{4}.$

В процессе преобразования применены законы алгебры логики, когда дизъюнкция переменной и её инверсии тождественно равна единице $(X_{3}\vee {\overline {X}}_{3})\equiv 1$,

а конъюнкция любой переменной с логической «1» равна самой переменной. В данном случае

${\overline {X}}_{1}X_{2}X_{4}\cdot 1={\overline {X}}_{1}X_{2}X_{4}$.

Существуют и другие способы минимизации логических функций, например, карты Карно, которые первоначально (в 1952 году) были предложены американским учёным Эдвардом Вейчем, а в 1953 году были усовершенствованы физиком Морисом Карно и получили название по его имени. Карты Карно — это координатный способ представления булевых функций. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются посредством кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

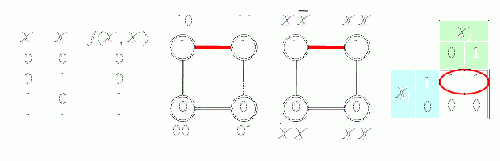
На рисунке ниже изображена простая таблица истинности для функции от двух переменных, соответствующий этой таблице квадрат с обозначением членов дизъюнктивной нормальной формы и эквивалентная таблица (карта) для группировки соседних элементов:

Таблица истинности для двух переменных и эквивалентная карта Карно для группировки соседних элементов

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. Карта Карно по своей сути — это представленная в развёрнутом виде таблица истинности. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!