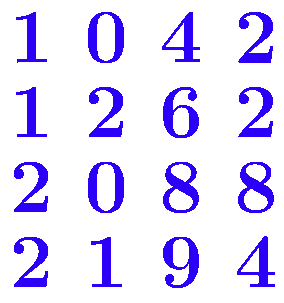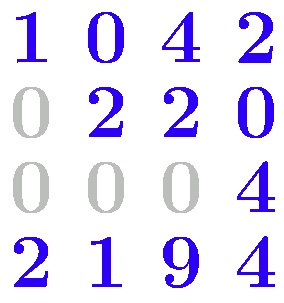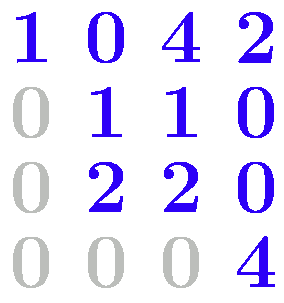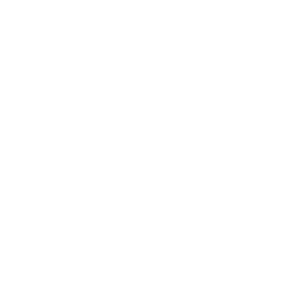Метод Гаусса
Ме́тод Га́усса — это фундаментальный алгоритм базовой алгебры, который применяют для работы с системами линейных уравнений путём последовательного исключения переменных. Этот метод, названный в честь немецкого математика Карла Фридриха Гаусса, также используется для вычисления определителей, матриц и других задач.
История
История метода Гаусса уходит корнями в древность, когда китайские математики использовали похожие методики для работы с системами линейных уравнений. В трактате «Девять глав о математическом искусстве», датируемом II веком до н.э., описывается метод решения систем уравнений, напоминающий современный метод Гауcса.
Европейские математики начали разрабатывать подобные методы в XVII–XVIII веках. Иcаак Ньютон[1] в своей работе «Универсальная арифметика» (1707) представил идеи, схожие с методом исключения переменных. Алексис Клод Клеро в 1750 году применил метод последовательного исключения.
Гениальный математик Карл Фридрих Гаусс впервые применил свой одноимённый метод в 1799 году, совершив прорыв в астрономических вычислениях при определении траектории движения астероида Церера. Интересно, что сам Гаусс не спешил обнародовать своё открытие. Лишь спустя почти три десятилетия, в 1827 году, французский математик Жан-Батист Жозеф Фурье представил миру первое печатное описание этого революционного подхода.
Новаторское использование Гауссом своего метода в 1810 году для оптимизации погрешностей геодезических измерений заложило фундамент метода наименьших квадратов. Это новшество значительно расширило сферу применения гауссовского подхода, выведя его за рамки теоретической математики в область практических расчётов и инженерных задач.
Эволюция метода Гаусса продолжилась благодаря вкладу других выдающихся математиков. Особо стоит отметить Вильгельма Йордана, который в 1888 году предложил усовершенствованную версию алгоритма, известную как метод Гаусса-Жордана. Эта модификация не только решала системы уравнений, но и открыла возможность эффективного вычисления обратных матриц.
С наступлением эры вычислительной техники в XX веке метод Гаусса стал краеугольным камнем множества алгоритмов в линейной алгебре. Его различные вариации, включая метод Гаусса-Зейделя, разработанный в 1874 году, обрели широкое признание и активно применяются в современной вычислительной математике, демонстрируя удивительную адаптивность и эффективность классического подхода в новых технологических реалиях.
Описание
Метод Гаусса представляет собой алгоритм решения систем линейных алгебраических уравнений путём последовательного исключения переменных. Суть метода заключается в преобразовании исходной системы уравнений[2] к эквивалентной системе треугольного вида, из которой легко найти значения неизвестных.
Процедура метода Гаусса включает два ключевых этапа: поступательное преобразование и регрессивное решение. На стадии поступательного преобразования система уравнений трансформируется в ступенчатую форму посредством последовательной элиминации переменных. Этот процесс реализуется через ряд элементарных операций: масштабирование уравнений, их комбинирование и перегруппировку.
Поступательное преобразование можно образно представить как «очищение» системы, где мы планомерно избавляемся от избыточных переменных в каждом уравнении, начиная с верхнего. По завершении этой фазы система приобретает характерную «каскадную» структуру, где каждое нижестоящее уравнение содержит на одну переменную меньше предшествующего.
Фаза регрессивного решения инициируется с последнего уравнения, содержащего единственную неизвестную. Двигаясь в обратном направлении, мы последовательно определяем значения всех переменных. Этот процесс напоминает разгадывание многоуровневой головоломки - начиная с простейшего элемента, мы постепенно раскрываем всю структуру.
Рассмотрим пример: 2x + y = 5 x - y = 1
Поступательное преобразование: умножаем второе уравнение на 2 и вычитаем из первого: 2x + y = 5 2x - 2y = 2
3y = 3
Теперь мы получили уравнение, содержащее только переменную y.
Регрессивное решение: из полученного уравнения находим y = 1, затем подставляем это значение в первое уравнение и вычисляем x = 2.
Этот пошаговый подход иллюстрирует элегантность и эффективность метода Гаусса в
Алгоритм
Метод Гаусса реализуется несколькими алгоритмами, каждый из которых имеет свои особенности и области применения.
Классический метод Гаусса предполагает последовательное исключение переменных из уравнений системы. Алгоритм включает два этапа: прямой ход (приведение матрицы к верхнетреугольному виду) и обратный ход (нахождение значений неизвестных). На каждом шаге прямого хода выбирается ведущий элемент — первый ненулевой элемент в текущем столбце. Затем производится обнуление элементов под ведущим элементом путём вычитания соответствующих строк. Этот метод эффективен для небольших систем, но может быть неустойчив к ошибкам округления при работе с большими матрицами[3].
Модифицированный метод Гаусса с селекцией опорного элемента представляет собой усовершенствованную версию классического алгоритма, нацеленную на повышение его числовой стабильности. В ходе каждой итерации в качестве ключевого выбирается элемент с максимальным абсолютным значением либо в текущей колонке, либо во всём оставшемся сегменте матрицы. Данный подход позволяет минимизировать погрешности округления и существенно улучшить точность конечного результата. Однако такая стратегия требует дополнительных вычислительных ресурсов для поиска опорного элемента, что неизбежно увеличивает алгоритмическую сложность метода.
Расширенная версия классического подхода — метод Гаусса-Жордана - предполагает приведение матрицы к диагональной форме. В этой модификации прямая и обратная фазы объединяются: после нуллификации элементов под главной диагональю производится обнуление элементов над ней. Результатом становится единичная матрица, а решение системы непосредственно отражается в правой части преобразованной матрицы. Этот метод особенно удобен при одновременном решении нескольких систем с идентичной матрицей коэффициентов, а также для вычисления обратной матрицы.
LU-декомпозиция представляет собой алгоритм, основанный на факторизации исходной матрицы в произведение нижней (L) и верхней (U) треугольных матриц. Данный метод демонстрирует высокую эффективность в ситуациях, когда необходимо решить множество систем с одинаковой матрицей коэффициентов, но различными векторами свободных членов. После однократного выполнения LU-декомпозиции решение каждой последующей системы сводится к последовательному разрешению двух простых треугольных систем.
Для работы с масштабными системами уравнений применяется блочный вариант метода Гаусса. В этом случае матрица разбивается на блоки, и операции выполняются над этими блоками как над целостными элементами. Такой подход позволяет оптимально использовать кэш-память вычислительной системы и эффективно распараллеливать процесс вычислений, что приобретает особую значимость при обработке больших массивов данных.
Каждый из описанных алгоритмов обладает своими уникальными преимуществами и ограничениями, связанными с числовой устойчивостью, скоростью выполнения и объёмом потребляемой памяти. Выбор конкретного метода зависит от специфики решаемой задачи, доступных вычислительных мощностей и требуемого уровня точности результата.
Применение в программировании
Метод Гаусса, также известный как метод исключения Гаусса или метод Гаусса-Жордана, широко применяется в различных областях программирования для решения систем линейных уравнений. Этот алгоритм особенно эффективен при работе с большими массивами данных и сложными математическими моделями.
В численных методах программирования метод Гаусса используется для решения систем линейных алгебраических уравнений (СЛАУ). Реализация алгоритма включает в себя прямой ход, где матрица коэффициентов приводится к треугольному виду, и обратный ход, где находятся значения неизвестных. Программисты часто оптимизируют этот процесс, используя различные техники, такие как выбор главного элемента по столбцу или строке для повышения точности вычислений.
В области компьютерной графики метод Гаусса находит применение при обработке изображений и трёхмерном моделировании. Например, при решении задач интерполяции и аппроксимации поверхностей, что критично для создания реалистичных текстур и моделей в играх и анимации. Программисты используют модифицированные версии метода Гаусса для оптимизации производительности рендеринга сложных сцен.
В машинном обучении и анализе данных метод Гаусса применяется для решения задач линейной регрессии и классификации. Программисты реализуют его в алгоритмах обучения нейронных сетей, особенно при работе с линейными слоями и оптимизации весов. Эффективная реализация метода Гаусса позволяет ускорить процесс обучения моделей на больших датасетах[4].
В криптографии и теории кодирования метод Гаусса используется для анализа и дешифрования линейных криптосистем. Программисты применяют его при реализации алгоритмов коррекции ошибок в системах передачи данных, таких как код Рида-Соломона. Это особенно важно для обеспечения надёжности коммуникаций в условиях зашумлённых каналов связи.
Достоинства и недостатки метода Гаусса
Метод Гаусса обладает рядом существенных преимуществ в области вычислительной математики и программирования. Одним из ключевых достоинств является его универсальность — система применима к широкому спектру задач базовой алгебры, от решения систем линейных уравнений до вычисления определителей и обратных матриц. Это позволяет использовать единый подход для различных вычислительных задач, упрощая реализацию и поддержку программного кода.
Эффективность метода Гаусса проявляется в его вычислительной сложности, которая составляет O(n^3) для матрицы размером n×n. Это делает его более быстрым по сравнению с некоторыми альтернативными методами, особенно для систем среднего размера. Программисты ценят метод за его предсказуемое время выполнения, что критично при разработке систем реального времени.
Важным преимуществом является возможность параллельной реализации метода Гаусса. Современные многоядерные процессоры и графические ускорители позволяют значительно ускорить вычисления за счёт одновременной обработки различных частей матрицы. Это особенно актуально при работе с большими объёмами данных в научных расчётах и машинном обучении.
Однако метод Гаусса не лишён недостатков. Одной из основных проблем является накопление ошибок округления при работе с числами с плавающей точкой[5]. Это может привести к значительным неточностям в результатах, особенно для плохо обусловленных матриц. Программисты вынуждены применять дополнительные техники, такие как частичный выбор главного элемента, что усложняет реализацию и может снижать производительность.
Метод Гаусса также демонстрирует ограниченную эффективность при работе с разреженными матрицами, где большинство элементов равны нулю. В таких случаях специализированные алгоритмы, учитывающие структуру разреженности, могут оказаться значительно быстрее. Это ограничивает применение метода Гаусса в некоторых областях, таких как анализ больших сетей или решение уравнений в частных производных.
Устойчивость метода Гаусса
Устойчивость метода Гаусса определяется его способностью сохранять точность вычислений при наличии ошибок округления и неточностей входных данных. Ключевым фактором, влияющим на устойчивость, является обусловленность матрицы коэффициентов системы линейных уравнений. Плохо обусловленные матрицы, характеризующиеся большим числом обусловленности, могут приводить к значительным ошибкам в результатах даже при небольших изменениях входных данных.
Проблема неустойчивости особенно проявляется при работе с числами с плавающей точкой в компьютерных вычислениях. Ошибки округления, возникающие на каждом шаге алгоритма, могут накапливаться и приводить к существенным отклонениям в конечном результате. Это особенно критично для систем большой размерности, где количество арифметических операций значительно возрастает.
Для повышения устойчивости данного метода применяются различные вариации алгоритма. Метод частичного выбора главного элемента (partial pivoting) предполагает выбор максимального по модулю элемента в текущем столбце в качестве ведущего элемента на каждом шаге исключения. Это позволяет минимизировать ошибки округления и улучшить численную стабильность алгоритма.
Более радикальным подходом является полный выбор главного элемента (full pivoting), где ведущий элемент выбирается как максимальный по модулю среди всех оставшихся элементов матрицы. Хотя этот метод обеспечивает лучшую устойчивость, он требует значительно больше вычислительных ресурсов и редко используется на практике из-за своей сложности.
В программной реализации метода Гаусса устойчивость может быть повышена за счет использования расширенной точности вычислений. Применение чисел двойной или четверной точности позволяет уменьшить влияние ошибок округления, хотя и за счет увеличения объёма вычислений и потребляемой памяти. В критических приложениях, требующих высокой точности, могут использоваться библиотеки произвольной точности[6], обеспечивающие контроль над точностью вычислений на каждом этапе.