Явления переноса

Процесс диффузии (одного из явлений переноса) двух различных типов частиц, в единой макросистеме

Явления переноса — процессы, происходящие в термодинамических системах при неизменных внешних условиях, возникающие при переходе таких систем к равновесному состоянию. К трем основным явлениям переноса в термодинамике относятся диффузия (перенос частиц), внутреннее трение или вязкость (перенос импульса) и теплопроводность (перенос энергии).

Общее описание явлений

Явления переноса основаны на двух принципах: законы сохранения энергии и импульса, а также определяющие уравнения (материальные соотношения). Законы сохранения энергии и импульса, которые в контексте явлений переноса формулируются как уравнения непрерывности, описывают, как должна сохраняться изучаемая величина. Материальные соотношения описывают, как величина реагирует на различные внешние воздействия посредством переноса.

Так как молекулы газа находятся в непрерывном тепловом движении, то постоянную скорость молекула сохраняет лишь до столкновения с другой молекулой. Столкновения молекул друг с другом стремятся выровнять распределение параметров системы в пространстве. В теории явлений переноса важную роль играет средняя длина свободного пробега <l> — среднее расстояние, которое молекула проходит между двумя последовательными столкновениями с другими молекулами.

Можно показать, что ${\textstyle <l>={1 \over {\sqrt {2\pi \sigma ^{2}n}}}}$, где

σ — эффективный диаметр молекул, n — концентрация молекул.

Промежутки времени между двумя последовательными соударениями изменяются хаотически, но можно ввести среднюю частоту соударений <z>, то есть среднее число соударений, испытываемое молекулой за единицу времени:

$<z>={v \over <l>}$, где

v — средняя скорость теплового движения.

Диффузия

Явления переноса в термодинамически неравновесных системах — это необратимые процессы, в результате которых происходит пространственный перенос энергии, массы или импульса. Термодинамически равновесное состояние системы это такое состояние теплового и механического равновесия структурных элементов системы, которое без внешнего воздействия может сохраняться сколь угодно долго. В данном случае неравновесным состоянием системы считается обратное состояние — состояние макроскопической системы, изменяющееся или способное изменяться спонтанно (без внешнего воздействия). В неравновесном состоянии системы в разных её частях могут быть различны термодинамические параметры — температура и давление. Неравновесные термодинамические системы также могут характеризоваться набором двух или нескольких состояний локального термодинамического равновесия. В термодинамике диффузия — явление самопроизвольного взаимного проникновения и перемешивания частиц (в частности, молекул) двух соприкасающихся веществ (газов, жидкостей, твердых тел). Встречается также самодиффузия, когда частица движется среди ей подобных. Условием диффузии или самодиффузии является неоднородное распределение частиц в пространстве, иначе говоря, наличие градиента концентрации частиц. Происходит перенос частиц из области с большей концентрацией в область, где концентрация меньше.

Уравнение диффузии (закон Фика) имеет вид:

$J_{N}=-D{dn \over dz}S$, где

$J_{N}$ — диффузионный поток частиц, то есть число частиц, прошедших за единицу времени в результате диффузии через поверхность площадью S, перпендикулярную к оси OZ,

${dn \over dz}$ — градиент концентрации вдоль этой оси, D — коэффициент диффузии.

Для идеального газа коэффициент диффузии D может быть рассчитан из соотношения:

$D={1 \over 3}v<l>$

В жидкости диффузионное движение частицы состоит из случайных перемещений на расстояния порядка размера самой частицы и малых колебаний около вре́менных положений равновесия. В твёрдом теле диффузия затруднена фиксированным положением атомов среды, образующих кристаллическую решётку.

Диффузия играет важную роль во многих естественных явлениях и в технологических процессах.

Вязкость

В термодинамике вязкость — явление возникновения внутреннего трения между слоями газа или жидкости, движущимися параллельно с различными скоростями. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряющая сила и наоборот, медленно движущийся слой тормозит слой, движущийся быстрее.

Механизм внутреннего трения в жидкостях и газах заключается в том, что движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения.

Уравнение вязкости (закон Ньютона):

$J_{p}=-\eta {du \over dz}S$, где

$J_{p}$ — поток импульса, то есть импульс направленного движения, перенесённый за единицу времени через поверхность площадью S, перпендикулярную к оси OZ,

${du \over dz}$ — градиент скорости направленного движения, η — коэффициент динамической вязкости.

Скорость движения слоёв направлена перпендикулярно оси OZ, по касательной к поверхности соприкосновения слоёв S. Поток импульса равен силе внутреннего трения между слоями.

Для идеального газа коэффициент динамической вязкости η может быть рассчитан из соотношения:

$\eta ={1 \over 3}\rho v<l>$, где

$\rho$ — плотность газа.

Вязкость газов увеличивается при нагреве, а вязкость жидкостей, наоборот, уменьшается. Это связано с различными молекулярными механизмами вязкости в этих системах. Различают два механизма переноса количества движения: кинетический (не предполагающий столкновений между молекулами) и столкновительный. Первый является преобладающим в разреженном газе, второй – в плотном газе и жидкости.

Вязкость жидкостей, где расстояние между молекулами много меньше, чем в газах, обусловлена в первую очередь межмолекулярными взаимодействиями, ограничивающими подвижность молекул.

Динамическая вязкость

Очевидно, что коэффициент динамич руктурных единиц системы,

E — энергия активации,

k — постоянная Больцмана, равная 1,38 × 10^-23 Дж/К,

T — температура.

Динамическая вязкость является одним из основных структурно-чувствительных свойств различных жидких смесей, а том числе металлических расплавов.

Кинематическая вязкость

В различных практических приложениях, в том числе при расчёте различных гидродинамических узлов, материаловедении и высокотемпературной металлургии, широкое распространение получила кинематическая вязкость — величина, связанная с динамической вязкостью и плотностью рассматриваемой системы:

$\nu ={\eta \over \rho }$, где

$\rho$ — плотность системы.

Кинематическая вязкость — свойство часто рассматриваемое при изучении металлических расплавов.

Теплопроводность

Процесс передачи теплоты от более нагретой среды к менее нагретой

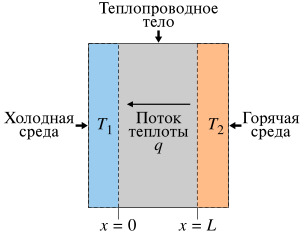
В термодинамике теплопроводность — перенос тепловой энергии из области с более высокой температурой в область, где температура ниже, посредством хаотического движения частиц. В газе перенос энергии происходит за счет того, что молекулы, попавшие из нагретой области газа в более холодную, отдают избыток своей кинетической энергии окружающим частицам, а молекулы, попавшие из холодной области в более нагретую, увеличивают свою кинетическую энергию за счет окружающих частиц.

Уравнение теплопроводности (закон Фурье):

$J_{Q}=-\lambda {dT \over dz}S$, где

$J_{Q}$ — поток теплоты, то есть количество теплоты, прошедшее за единицу времени посредством теплопроводности через поверхность площадью S, перпендикулярную к оси OZ,

${dT \over dz}$ — градиент температуры вдоль этой оси, λ — коэффициент теплопроводности.

Для идеального газа коэффициент теплопроводности может быть найден из соотношения:

$\lambda ={{1 \over 3}\cdot c_{V}\cdot \rho \cdot v\cdot <l>}$, где

$c_{V}$ — удельная теплоёмкость газа при постоянном объёме.

В жидкостях среднее расстояние между частицами сравнимо с размерами частиц, а их средняя кинетическая энергия соизмерима со средней потенциальной энергией межатомного (межмолекулярного) взаимодействия, что ускоряет процесс теплопроводности.

В твёрдых телах теплопроводность зависит от физической природы этих тел. Явление теплопроводности обусловило создание таких технических устройств как радиаторы охлаждения.

Связь между коэффициентами переноса

Для коэффициентов теплопроводности и вязкости следует, что между ними существует соотношение:

$\lambda =c_{V}\eta$.

Это уравнение устанавливает связь между чисто механическими и тепловыми явлениями в газе.

Если сравнивать выражения для коэффициентов вязкости и диффузии, следует, что они связаны соотношением:

$D={\eta \over \rho }$.

Eсли сравнивать выражения для коэффициентов диффузии и теплопроводности, то получим соотношение:

$D={\lambda \over \rho c_{V}}$.

Любой из коэффициентов переноса, определённый в эксперименте, позволяет оценить среднюю длину свободного пробега молекулы, а следовательно, и размеры молекул.