Белый шум
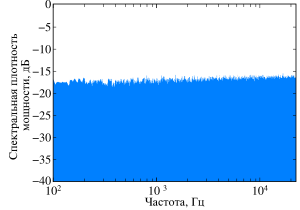
Бе́лый шум (стохастический сигнал с равномерным распределением энергии по всему частотному спектру) — математическая модель случайного процесса, характеризующаяся постоянной спектральной плотностью мощности на всех частотах[1].
Математическое определение и свойства
Фундаментальное описание белого шума основывается на концепции автокорреляционной функции. Автокорреляционная функция белого шума представлена в виде дельта-функции Дирака. Дельта-функция Дирака — это обобщённая функция, которая равна нулю везде, кроме одной точки, где она стремится к бесконечности[2].
Математическое выражение автокорреляционной функции записывается как B(τ)=σ2δ(τ). В данной формуле σ2 обозначает дисперсию процесса — меру разброса случайной величины относительно её математического ожидания. Символ δ(τ) представляет дельта-функцию, зависящую от временного сдвига τ.
Преобразование Фурье от дельта-функции даёт константу. Преобразование Фурье — это математическая операция, переводящая функцию времени в функцию частоты. Результатом применения преобразования Фурье к дельта-функции становится равномерность спектральной плотности мощности G(ω)=σ2 во всём частотном диапазоне.
Энергетические характеристики
Средняя мощность идеального белого шума стремится к бесконечности. Математическое интегрирование спектральной плотности мощности по всему частотному диапазону от минус бесконечности до плюс бесконечности даёт расходящийся интеграл. Расходящийся интеграл — это интеграл, значение которого стремится к бесконечности.
Физическая нереализуемость идеального белого шума требует ограничения частотного диапазона. Практическое применение возможно при условии существенного превышения ширины полосы шумового сигнала над полосой пропускания исследуемой системы.
В ограниченной полосе частот B средняя мощность составляет PB=2σ2B=N0B. Величина N0/2 представляет стандартное обозначение дисперсии в радиотехнических расчётах. Отношение энергии бита к спектральной плотности шума Eb/N0 служит ключевой характеристикой качества цифровых систем связи[3].
Математические модели
Дискретные представления
Дискретная модель белого шума формируется как последовательность статистически независимых случайных величин. Статистическая независимость случайных величин означает, что знание значения одной величины не даёт информации о значениях других величин.
Программная реализация использует генераторы псевдослучайных чисел. Псевдослучайные числа — это детерминированная последовательность чисел, обладающая статистическими свойствами случайных чисел. Алгоритмическая формула создаёт равномерное распределение значений от −1 до 1.
Бинарные варианты ограничиваются значениями +1 и −1. Бинарный сигнал сохраняет свойство белизны при условии статистической некоррелированности последовательности. Дискретный стохастический процесс W(n) характеризуется нулевым математическим ожиданием E[W(n)]=0.
Автокорреляционная функция дискретного белого шума выражается как RW(n)=σ2δ(n). Дискретная дельта-функция равна σ2 при n=0 и равна нулю при всех остальных значениях n[4].
Непрерывные модели
Стационарные и нестационарные варианты белого шума различаются временной зависимостью дисперсии σ2. Стационарный процесс имеет статистические характеристики, не изменяющиеся во времени. Нестационарный процесс характеризуется изменением статистических параметров в зависимости от времени.
Непрерывная функция w(t) требует определения через интегральные характеристики. Математические сложности точечного задания связаны с необходимостью работы с обобщёнными функциями. Интеграл W[a, a+r] по интервалу ширины r имеет дисперсию, пропорциональную длине интервала.
Дисперсия интеграла составляет (b−a)σ2. Ковариация между интегралами по пересекающимся интервалам пропорциональна ширине пересечения. Строгое математическое описание использует теорию стохастических темперированных распределений в функциональном пространстве S'(ℝ)[5].
Теорема Бохнера-Минлоса-Сазанова обеспечивает существование и единственность вероятностной меры в бесконечномерном пространстве. Характеристическая функция определяет вероятностное распределение через преобразование Фурье от плотности вероятности.
Векторные формы
Векторная форма белого шума определяется через диагональную ковариационную матрицу размерности n×n. Корреляционная матрица принимает вид единичной матрицы. Единичная матрица указывает на взаимную некоррелированность компонентов случайного вектора.
Многомерное нормальное распределение обладает сферической симметрией в n-мерном пространстве. Сферическая симметрия означает инвариантность распределения относительно поворотов координатных осей. Ортогональные преобразования сохраняют свойство белизны для гауссовских процессов.
Дискретное преобразование Фурье сохраняет белизну гауссовского шума. Быстрое преобразование Фурье (FFT) представляет эффективный алгоритм вычисления дискретного преобразования Фурье. Преобразование Хартли — альтернативный метод спектрального анализа с действительными коэффициентами.
Коэффициенты Фурье белого гауссовского шума образуют плоский спектр мощности. Спектральная плотность мощности Pi = σ2 остаётся постоянной для всех частотных компонентов[6].
Типология шумовых процессов
Гауссовы и негауссовы варианты
Понятия «белый» и «гауссовский» шум описывают различные характеристики случайного процесса. Белизна характеризует частотные свойства сигнала через равномерность спектральной плотности мощности. Гауссовость определяет статистическое распределение амплитудных значений сигнала[7].
Белый шум может следовать различным статистическим распределениям. Распределение Гаусса (нормальное распределение) характеризуется симметричной колоколообразной формой плотности вероятности. Распределение Пуассона описывает вероятность наступления редких событий за фиксированный интервал времени.
Цветовая классификация
Отдалённый шум водопада приобретает розовую окраску из-за неравномерного затухания частотных компонентов в воздухе. Высокочастотные составляющие звука ослабевают сильнее низкочастотных при распространении в атмосфере. Коэффициент поглощения звука в воздухе возрастает пропорционально квадрату частоты.
Розовый шум характеризуется равной энергией в каждой октаве. Октава — это частотный интервал, в котором верхняя граница в два раза превышает нижнюю. Спектральная плотность мощности розового шума обратно пропорциональна частоте.
Синий шум демонстрирует противоположную тенденцию с преобладанием высокочастотных компонентов. Спектральная плотность мощности синего шума возрастает пропорционально частоте. Звук /ʃ/ классифицируется как цветной шум из-за наличия формантной структуры[8].
Происхождение названия
Исследования Исаака Ньютона продемонстрировали, что белый свет содержит электромагнитные волны всех видимых частот[9]. Призматическое разложение белого света показывает непрерывный спектр от фиолетового до красного цвета. Аналогия с оптическими явлениями дала название шумовому сигналу с равномерным частотным спектром.
Диапазон слышимых частот от 20 до 20 000 Гц определяет область практического применения понятия белого шума в акустике. Нижняя граница соответствует порогу восприятия низкочастотных колебаний человеческим ухом. Верхняя граница определяется возрастными изменениями слуховой системы и индивидуальными особенностями.
За пределами слышимого диапазона термин «белый шум» сохраняет математический смысл без физиологического восприятия. Ультразвуковые и инфразвуковые колебания могут обладать характеристиками белого шума в соответствующих частотных областях.
Практические применения
Техническое использование
Белый шум служит испытательным сигналом для измерения частотных характеристик линейных систем. Линейная система подчиняется принципу суперпозиции — реакция на сумму входных сигналов равна сумме реакций на каждый сигнал в отдельности. Частотная характеристика описывает зависимость амплитуды и фазы выходного сигнала от частоты входного сигнала.
Усилители электрических сигналов тестируются подачей белого шума на вход с последующим спектральным анализом выходного сигнала. Электронные фильтры проверяются на соответствие проектных характеристик полосы пропускания и коэффициента передачи. Дискретные системы управления анализируются в цифровом домене с использованием дискретного белого шума.
Генераторы случайных чисел используют шумовые процессы как источник энтропии. Энтропия в теории информации измеряет степень неопределённости случайного процесса. Высокая энтропия обеспечивает непредсказуемость генерируемых последовательностей.
Операционная система Linux содержит утилиту speaker-test для генерации белого или розового шума[10]. Тестирование акустических систем предпочтительно проводить розовым шумом из-за более равномерного распределения энергии по октавам в логарифмическом масштабе частот.
Акустические применения
Архитектурная акустика применяет генерацию стационарного белого шума малой мощности для маскировки нежелательных звуков. Маскировка звука — это психоакустический эффект, при котором один звук делает неслышимым другой звук. Стационарность шумового сигнала означает постоянство его статистических характеристик во времени.
Внутренние пространства зданий характеризуются специфической акустической средой с множественными отражениями и реверберацией. Реверберация — это процесс постепенного затухания звука в закрытом помещении после прекращения его излучения источником.
Электронная музыка использует белый шум как инструмент звукового синтеза и материал для формирующих фильтров. Субтрактивный синтез начинается с шумового сигнала, богатого гармониками, который затем обрабатывается фильтрами для получения нужного тембра.
Синтез ударных инструментов опирается на высокое содержание шумовых компонентов в частотном спектре. Тарелки и другие металлические ударные инструменты производят звуки с широким частотным спектром, приближающимся к характеристикам окрашенного шума[11].
Примечания
- ↑ Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи: учебник для вузов. — М.: Радио и связь, 1999. — 432 с.
- ↑ Учебное пособие СибЛЭК // Белый шум и его характеристики. Радиотехнические цепи и сигналы. — М., 2018.
- ↑ Сигов А.С., Нефедов В.И. Белый шум и его характеристики. Теория электросвязи. — М.: Высшая школа, 2015.
- ↑ Перов Б.Г., Черанёв М.А., Полторак В.П. Разработка математической модели канала связи с белым гауссовым шумом // Молодой ученый. — 2013. — № 6 (53). — С. 116—121.
- ↑ Durrett R. Probability: Theory and Examples (англ.). — 5th edition. — Cambridge University Press, 2019. — 419 p.
- ↑ Романов А.Ю., Панчул Ю.В. (ред.). Цифровой синтез: практический курс. — М.: ДМК Пресс, 2020. — 556 с.
- ↑ гл. ред. Ю. С. Осипов: Белый шум. Большая российская энциклопедия : [в 35 т.]. М.: Большая российская энциклопедия (2004–2017). Архивировано 15 июня 2022.
- ↑ Fox R.A., Jacewicz E. Spectral dynamics of sibilant fricatives are contrastive and language specific (англ.) // Journal of the Acoustical Society of America. — 2016. — Vol. 140, no. 4. — P. 2518–2529.
- ↑ Ньютон И. Оптика или трактат об отражениях, преломлениях, изгибаниях и цветах света / Пер. С. И. Вавилова. — М.: Гос. изд-во техн.-теорет. лит., 1954. — 365 с.
- ↑ Tranter J. Introduction to Sound Programming with ALSA (англ.) // Linux Journal. — 2004. October.
- ↑ Виртуальный полифонический аналоговый синтезатор на основе субтрактивного синтеза // Журнал Научный аспект. — 2013. — № 3.
Ссылки
- Rational Acoustics (англ) Why is My Noise Pink? Noise Contours Explained. — 2021.
- Sweetwater (англ) Pink Noise Versus White Noise Acoustic FieldsSweetwater // InSync Magazine. — 2020.
- EdUHK Phonetics (англ) Acoustic Aspects of Consonants // English Pronunciation Guide. — Hong Kong, 2022.