Алгоритм искусственной стаи рыб

Алгори́тм иску́сственной ста́и рыб (Artificial Fish Swarm, Fish Swarm Algorithm) отбора признаков — эволюционный оберточный, рандомизированный метод решения задачи отбора признаков в машинном обучении, основанный на моделировании поведения стаи рыб при поиске пищи в естественной среде

Свойства и структура алгоритма

Ниже описаны свойства и структура алгоритма искусственной стаи рыб.

Общее описание алгоритма

В естественной среде стая рыб является примером самоорганизующегося сообщества без лидера, основная цель которого — найти место с наивысшей концентрацией пищи. На основании аналогии для решения произвольных задач оптимизации в 2002 году был создан исходный вариант алгоритма искусственной стаи рыб. С тех пор появилось много модификаций метода, их обзор представлен в работе «A Review of Artificial Fish Swarm Optimization Methods and Applications»).

Адаптация метода к задаче отбора признаков предполагает симуляцию поведения единичной части популяции (искусственной рыбы) путем выбора на каждой итерации одной из трёх стратегий поведения:

• стратегии поиска (рыба самостоятельно ищет место с большей концентрацией пищи);
• стратегии роевого поведения (рыба стремится к центру роя);
• стратегии следования (рыба стремится к другому участнику стаи, который находится в месте с большей концентрацией пищи).

Входные и выходные параметры алгоритма

На вход алгоритма искусственной стаи рыб подаётся:

• вектор значений зависимой переменной, матрица значений независимых переменных (признаков);
• используемая метрика качества решения исходной задачи (например, для задачи регрессии это может быть коэффициент детерминации, для задачи классификации — показатель точности (accuracy));
• используемая метрика нахождения расстояния между двумя рыбами.

Внутри алгоритма реализуется выбранный метод решения исходной задачи (например, для задачи регрессии это может быть метод наименьших квадратов, для задачи классификации — логистическая регрессия).

Также необходимо задать несколько технических параметров:

• n — количество рыб в стае;
• Step (шаг) — расстояние, которое проходит рыба при реализации стратегии поиска за одну итерацию;
• Visual (зона видимости) — расстояние, в пределах которого рыба видит соседей по стае;
• try_number (число попыток) — параметр стратегии поиска, определяющий, сколько раз рыба попытается изменить своё местоположение для нахождения места с большей концентрацией пищи;
• δ (показатель плотности) — параметр, являющийся одним из триггеров переключения на стратегию роевого поведения — если рыба видит меньшую долю стаи, чем указано данным параметром, то данное переключение возможно.

Результатом работы алгоритма является вывод бинарного вектора Χ размерами 1×m, где m — количество столбцов в матрице признаков, отражающее лучшую комбинацию выбранных признаков, и значение метрики качества решения исходной задачи для лучшей комбинации признаков.

Значение элементов бинарного вектора отражает выбор или отсутствие выбора соответствующего признака. Например, для случая 5 рассматриваемых признаков вектор Х = (0,1,0,0,1) означает, что лучшее решение задачи регрессии/классификации обеспечивает лишь совместное использование 2-го и 5-го признаков в качестве независимых при неиспользовании всех остальных.

Структура алгоритма

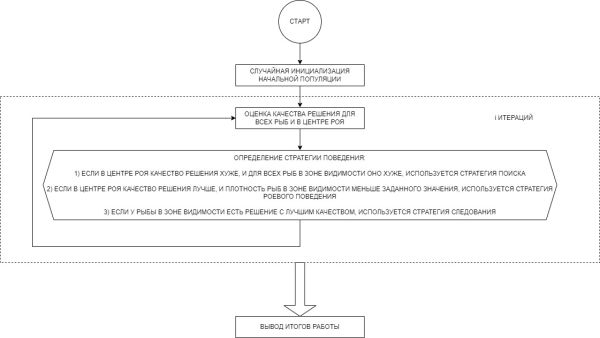
Общая схема работы алгоритма представлена на рисунке ниже

Описание работы алгоритма

Дана матрица независимых переменных Х размером t (количество наблюдений)×m (количество признаков) и вектор значений независимых переменных Y размером t×1.

На первом шаге работы алгоритма происходит случайная инициализация n бинарных векторов длиной m (каждый вектор является «рыбой»), отражающих выбор тех или иных признаков.

Например, вектор $V_{11}=(0,0,1,0,1,0,0,0,0,1)$ показывает, что первая «рыба» выбирает в качестве зависимых переменных в модели 3,5 и 10 переменную.

Оценка качества решения происходит путем построения соответствующих моделей — например, для задачи регрессии строится n моделей (со своей комбинацией переменных), по каждой из которых рассчитывается показатель качества (коэффициент детерминации для задач регрессии или, например, F1-критерий для задач классификации). Величина этого показателя является математическим аналогом величины концентрации пищи.

На каждой итерации рассчитывается «центр роя рыб» — бинарный вектор ${V_{i}}$, максимально равноудаленный от всех «рыб» на i-й итерации, и рассчитывается метрика качества в нем.

Далее для каждой рыбы происходит определение стратегии поведения:

• если в центре роя метрика качества лучше, то происходит движение к центру по формуле ${V_{(i+1)j}=V_{ij}+{\frac {V_{i}-V_{ij}}{|V_{i}-V_{ij}|}}\times Step}$, где $|V_{i}-V_{ij}|$ — расстояние между конкретной «рыбой» и центром на i-й итерации;

• если для некоторой «рыбы» на расстоянии меньше величины Visual находится лучшее решение, то происходит движение к этому лучшему решению аналогично формуле выше: ${V_{(i+1)j}=V_{ij}+{\frac {V_{b}-V_{ij}}{|V_{b}-V_{ij}|}}\times Step}$, где ${V_{b}}$ — «рыба» с лучшим значением метрики качества;

• если «рыба» не выбирает ни стратегию роевого поведения, ни стратегию следования, она переходит на стратегию поиска — от текущего положения $V_{ij}$ «рыба» отходит не больше try_number раз не больше чем на расстояние Visual для поиска более лучшей комбинации переменных.

Критерием остановки алгоритма могут выступать:

• достижение заданной точности алгоритма;
• достижение стабильности местоположения рыб.

Примечания

Данная статья имеет статус «готовой». Это не говорит о качестве статьи, однако в ней уже в достаточной степени раскрыта основная тема. Если вы хотите улучшить статью — правьте смело!