Аксиома
Аксио́ма (от древнегреческого ἀξίωμα, означающего «утверждение, положение», происходящего от άξιοω — «считаю достойным, настаиваю, требую»), также именуемая постула́том[1] (от латинского postulatum, буквально переводимого как «требуемое»[2]), представляет собой фундаментальное утверждение определённой теории. Данное утверждение принимается как истинное без необходимости доказательства в рамках рассматриваемой теории и служит основой для доказательства других положений этой теории, именуемых теоремами[3].
Назначение
Принятие аксиом без доказательств обусловлено индуктивным соображением: каждое доказательство базируется на определённых утверждениях, и требование доказательств для каждого из них приводит к бесконечной цепочке. Чтобы избежать этой бесконечности, необходимо прервать цепь, приняв некоторые утверждения в качестве исходных без доказательств. Эти исходные утверждения и называются аксиомами[4].
В современной научной практике вопрос истинности аксиом, лежащих в основе теории, разрешается либо в контексте других научных теорий, либо путём интерпретации данной теории[5].
Аксиоматиза́ция (или формализация) теории представляет собой чёткое определение конечного или счётного, рекурсивно перечислимого (как в аксиоматике Пеано) набора аксиом и правил вывода. После наименования изучаемых объектов, их основных отношений и установления аксиом, которым эти отношения должны соответствовать, дальнейшее изложение должно опираться исключительно на эти аксиомы, без обращения к обыденному пониманию этих объектов и их отношений.
Выбор аксиом, составляющих основу конкретной теории, не является единственно возможным. Примеры различных, но эквивалентных наборов аксиом встречаются в математической логике и евклидовой геометрии.
Набор аксиом считается непротиворечивым, если на его основе, используя правила логики, невозможно прийти к противоречию, то есть доказать одновременно некое утверждение и его отрицание.
Курт Гёдель, выдающийся математик из Австрии, сформулировал и доказал фундаментальные «теоремы о неполноте». Эти теоремы устанавливают, что для любой формальной системы, способной описать арифметику натуральных чисел с операциями сложения и умножения, существует принципиальное ограничение. А именно, такая система неизбежно оказывается неполной.
Неполнота системы проявляется в том, что в ней всегда найдутся математические утверждения, которые невозможно ни доказать, ни опровергнуть, опираясь исключительно на аксиомы данной системы. Причём количество таких неразрешимых в рамках системы утверждений бесконечно.
Примечательно, что среди этих недоказуемых утверждений обязательно присутствует и утверждение о непротиворечивости самой рассматриваемой формальной системы. Это следствие теорем Гёделя имеет глубокие философские и математические импликации.
История
Термин «аксиома» впервые упоминается в трудах Аристотеля (384-322 до н. э.) и проникает в математику из философии Древней Греции. Евклид разграничивает понятия «постулат» и «аксиома», не раскрывая их различий. Начиная с эпохи Боэция, постулаты интерпретируются как требования (petitio), а аксиомы — как общие понятия. Изначально слово «аксиома» трактовалось как «истина, самоочевидная по своей природе». В различных списках «Начал» Евклида классификация утверждений на аксиомы и постулаты неодинакова, их последовательность также варьируется. Вероятно, это объясняется различием во взглядах переписчиков на сущность этих понятий.
Представление об аксиомах как о неизменных самоочевидных истинах сохранялось на протяжении длительного периода. Так, в словаре Даля аксиома определяется как «очевидность, ясная по себе и бесспорная истина, не требующая доказательств».
Работы русского математика Николая Лобачевского о неевклидовой геометрии, впервые опубликованные в конце 1820-х годов, послужили стимулом к пересмотру восприятия аксиом. Ещё в студенческие годы Лобачевский предпринимал попытки доказать пятый постулат Евклида, но впоследствии отказался от этой идеи. Он пришёл к заключению, что пятый постулат представляет собой лишь произвольное ограничение, которое может быть заменено другим. Если бы пятый постулат Евклида поддавался доказательству, Лобачевский неизбежно столкнулся бы с противоречиями. Однако, несмотря на отсутствие наглядной очевидности, новая версия пятого постулата в полной мере выполняла функцию аксиомы, позволяя сформировать новую непротиворечивую геометрическую систему.
Первоначально концепции Лобачевского не получили признания (к примеру, академик Остроградский отзывался о них негативно). Впоследствии, когда Лобачевский опубликовал свои труды на иностранных языках, его работы привлекли внимание Гаусса, также имевшего определённые наработки в области неевклидовой геометрии. Гаусс косвенно выразил восхищение этими исследованиями. Подлинное признание геометрия Лобачевского обрела лишь спустя 10-12 лет после кончины автора, когда была доказана её непротиворечивость при условии непротиворечивости евклидовой геометрии. Это событие вызвало революционные изменения в математическом сообществе. Гильберт инициировал масштабный проект по аксиоматизации всей математики с целью доказательства её непротиворечивости. Его планам не суждено было осуществиться из-за последовавших теорем Гёделя о неполноте. Тем не менее, это послужило импульсом к формализации математики. В частности, были сформулированы аксиомы натуральных чисел и их арифметики, появились работы Кантора по созданию теории множеств. Эти достижения позволили математикам разрабатывать строго истинные доказательства теорем.
В современной математической и научной практике аксиомы рассматриваются не как автономные истины, а как ключевые структурные элементы теоретических построений. Их выбор может быть достаточно свободным и не ограничиваться критерием интуитивной очевидности. Основополагающим требованием к системе аксиом выступает исключительно её логическая согласованность.
При конструировании аксиоматического базиса теории учёные руководствуются преимущественно функциональными соображениями. Среди них: компактность формулировок, операциональное удобство, экономия исходных концептов. Такой утилитарный подход, однако, не обеспечивает гарантии абсолютной истинности принятых постулатов[3].
Философ науки Карл Поппер предложил критерий, согласно которому даже одно противоречащее наблюдение способно опровергнуть теорию, тем самым демонстрируя несостоятельность её аксиоматической основы. В то же время, многочисленные подтверждающие факты лишь усиливают вероятностную оценку корректности аксиоматической системы, но не обеспечивают её абсолютной достоверности.
Примеры аксиом
- Евклидова аксиома параллельности[6]
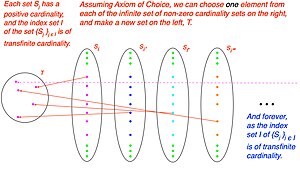
- Аксиома выбора;
- Аксиома Архимеда;
- Аксиома регулярности;
- Аксиома объёмности;
- Аксиома Колмогорова;
- Аксиома полной индукции;
- Аксиома множества подмножеств.
Примеры аксиоматических систем
- Аксиоматика теории множеств[7];
- Евклидова аксиоматика;
- Аксиоматическая система вещественных чисел;
- Аксиоматика Тарского;
- Аксиоматическая система Гильберта.
Примечания
- ↑ Постулат // Энциклопедический словарь Гранат: В 58 томах. — М., 1910—1948..
- ↑ Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с..
- ↑ 3,0 3,1 Под редакцией А.А. Ивина. Аксиома // Философия: Энциклопедический словарь. — М.: Гардарики. — 2004..
- ↑ Клайн Морис. «Математика. Утрата определённости.» — М.: Мир, 1984..
- ↑ Философский энциклопедический словарь. — М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983..
- ↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.—Л.: ГТТИ, 1948. — Т. I. — С. 15. Архивировано 6 апреля 2008 года. Архивированная копия. Дата обращения: 25 апреля 2008. Архивировано из оригинала 6 апреля 2008 года..
- ↑ Н. Бурбаки. Основания математики. Логика. Теория множеств // Очерки по истории математики / И. Г. Башмакова (перевод с французского). — М.: Издательство иностранной литературы, 1963. — С. 37—53. — 292 с. — (Элементы математики)..